12
Invariant Description for a Batch Version of the UCB Strategy with Unknown Control Horizon
We consider a batch processing variation of the UCB strategy for multi-armed bandits with a priori unknown control horizon size n. Random rewards of the considered multi-armed bandits can have a wide range of distributions with finite variances. We consider a batch processing scenario, when the arm of the bandit can be switched only after it was used a fixed number of times, and parallel processing is also possible in this case. A case of close distributions, when expected rewards differ by the magnitude of order N–1/2 for some fairly large N, is considered as it yields the highest normalized regret. Invariant descriptions are obtained for upper bounds in the strategy and for minimax regret. We perform a series of Monte Carlo simulations to find the estimations of the minimax regret for multi-armed bandits. The maximum for regret is reached for n proportional to N, as expected based on obtained descriptions.
12.1. Introduction
The multi-armed bandit (MAB) problem is a control problem in a random environment. Traditionally, it is pictured as a slot machine that has j (two or more) arms (levers). Choosing an arm at time n yields some random rewards (income) ξ(n) associated with it. The gambler (decision-making agent) begins with no initial knowledge about rewards associated with the arms.
The goal is to maximize the total expected reward.
A classic reinforcement learning problem that exemplifies the exploration– exploitation trade-off dilemma (Lattimore and Szepesvari 2020): the goal of a gambler is to maximize the total expected reward. Yet, as there is no prior knowledge about parameters of the MAB, the gambler should gather new data to lessen the losses due to incomplete knowledge (exploration) while getting the most income based on already obtained knowledge (exploration).
Formally, we describe a MAB as a controlled random process {ξ(n)}, n = 1,2, … (with a priori unknown control horizon). Value ξ(n) at time n only depends on the chosen arm. Expected values of the rewards m1, …, mJ are assumed to be unknown. Variances of the rewards D1, … , DJ are assumed to be known and equal (D1 = ⋯ = DJ = D). Examined MAB can therefore be described with a vector parameter θ = (m1, …, mJ).
The regret (loss function) after N rounds is defined as the expected difference between the reward sum associated with an optimal strategy and the sum of the collected rewards and is equal to
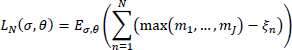
Here, Eσ, θ denotes the expected value calculated with respect to the measure generated by strategy σ and parameter θ.
Further, we consider the normalized regret (scaled by (Dn)-1/2, n is the reached step).
We assume mean rewards to have “close” distributions that can be described as values of parameters that are chosen as follows
This set of parameters describes “close” distributions: the difference between expected values has the order N-1/2. As control horizon size is a priori unknown, we use N as a parameter. Maximal normalized regrets are observed on that domain and have the order N1/2 (see Vogel 1960).
For “distant” distributions, the normalized regrets have smaller values. For example, they have order log N if max(m1, …, mJ) exceeds all other {ml} by some δ > 0 (see Lai et al. 1980).
We aim to build a batch version of the UCB strategy described in Lai (1987). Also, we obtain its invariant description on the unit horizon in the domain of “close” distributions (as in the case of “close” distributions, the maximum values of expected regret are attained). Finally, we show (using Monte Carlo simulations) that expected regret only depends on the number of processed batches (not the number of steps) and that the maximum of the scaled regret is reached for step number n proportional to N.
12.2. UCB strategy
Suppose that at the step n, the l-th arm was chosen nl times and let Xl(n) denote a corresponding cumulative reward (for l = 1, … , J).
Xl(n)/nl is a point estimator of the mean reward ml for this arm.
Since the goal is maximize the total expected reward, it might seem reasonable to always to apply the action corresponding to the current largest value Xl(n)/nl.
However, such a rule can result in a significant loss since initial estimate Xl(n)/nl, corresponding to the largest ml , can by chance take a lower value, and consequently, this action will be never applied.
To get a correct estimation for ml , we must ensure that each arm is chosen infinitely many times as n → ∞.
Instead of estimates of themselves, it is proposed to consider the upper bounds of their confidence intervals
It is supposed that for initial estimation of mean rewards, each arm will be used once in the initial stage of control.
12.3. Batch version of the strategy
We consider a setting in which the gambler can change the arm only after using it M times in a row. We assume for simplicity that N = MK, where K is the number of batches. This limitation allows batch (and also parallel) processing (see Kolnogorov 2012, 2018).
If M is large and variance is finite, then due to the central limit theorem, the reward for each batch will have a close to normal distribution with probability density function
if yn = l, and l = 1, … , J. Therefore, in this scenario, we can assume that we need to study a Gaussian MAB with J arms.
For the k-th batch, the following expression for the reward holds:
Upper bounds for batches take the form
where a is the parameter of the strategy, k is the number of processed batches, kl is the number of batches for which the l-th arm was chosen and Xl(k) is the corresponding cumulative reward after processing k batches (k = 1,2, … , K).
12.4. Invariant description with a unit control horizon
The aim is to get a description of the strategy and the regret, which is independent of the control horizon size. That way, it will be is possible to make conclusions about its properties no matter the horizon size. We aim to scale the step number by some parameter N (this parameter is the horizon size in the case where it is a priori known).
We denote by
the indicator of chosen action for processing the (k + 1)-th batch according to the considered rule (also recall that at k ≤ J every arm is chosen once for a batch, so Il(k) = 1 for k = l). With probability 1, only one of values of {Il(k)} is equal to 1.
The cumulative reward for each arm can be written as

where ![]() are i.i.d. normally distributed random variables with zero means and variances that are equal to MD. Note that for arm l the indicator equals 1 exactly kl times, so
are i.i.d. normally distributed random variables with zero means and variances that are equal to MD. Note that for arm l the indicator equals 1 exactly kl times, so ![]() is the sum of kl Gaussian random variables, which can be presented as a scaled by standard deviation, standard normal random variable. In that case
is the sum of kl Gaussian random variables, which can be presented as a scaled by standard deviation, standard normal random variable. In that case
where η ~ N(0,1) is a standard normal random variable.
The upper bound value for each arm can be written as (l = 1, 2, …, J; k = J + 1, J + 2, …, K):
Next, we apply a linear transformation that does not change the arrangement of bounds
And we introduce a notation t = kK-1, tl = klK-1, that way obtaining an expression
Here, t changes in interval (0, 1] when k changes from 1 to N, i.e. the control horizon is scaled to a unit size. A priori unknown control horizons can change from 0 to any value.
To obtain an invariant form for regret, we first assume without loss of generality that c1 = max(c1, …, cJ), so the regret can be expressed as
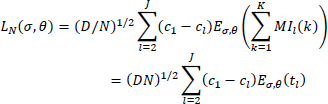
After normalization (scaling by (Dn)1/2), we get the following expression for

which is the required invariant description. Hence, we can present the results in the form of the following theorem.
THEOREM 12.1.– For Gaussian multi-armed bandits with J arms, fixed known variance D and unknown expected values m1, …, mJ that have “close” distributions defined by
the use of the batch UCB rule with bounds
results in an invariant description on the unit control horizon, which is described by
and normalized regret
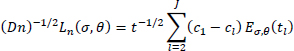
12.5. Simulation results
Having an invariant description allows us to generalize the results of Monte Carlo simulations for strategies at large.
In what follows, we consider a Gaussian two-armed bandit with control horizon sizes up to n = 10,000, which can be considered fairly large. We consider different values of N shown by different line colors. All of the results are averaged over 10,000 simulations.
Different plots (Figures 12.1–12.3) correspond to different values of difference between mean rewards of bandit arms. All the plots show maximum regret (scaled by (Dn)1/2) versus step number n.
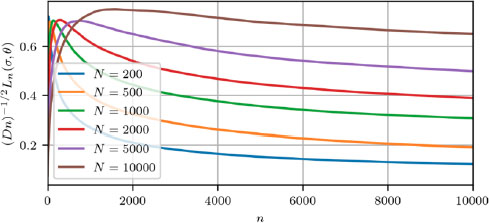
Figure 12.1. Maximum scaled regret versus step number for c2 − c1 = 10. For a color version of this figure, see www.iste.co.uk/zafeiris/data1.zip
Values of differences are chosen c2 − c1 = 3.3 (Figure 12.2) as in this case the biggest maximum regret was obtained according to Garbar (2020a, 2020b). Other values (c2 − c1 = 10, Figure 12.1; c2 − c1 = 1, Figure 12.3) correspond to bigger and smaller difference values for the expected reward.
For all cases, we can observe that the maximum for scaled regret is reached for n proportional to N. When the difference in mean rewards is large (Figure 12.1), the strategy can distinguish between better and worse arms in the early stages of control and regret is not that big.
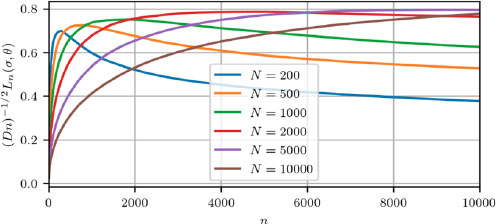
Figure 12.2. Maximum scaled regret versus step number c2 − c1 = 3.3. For a color version of this figure, see www.iste.co.uk/zafeiris/data1.zip
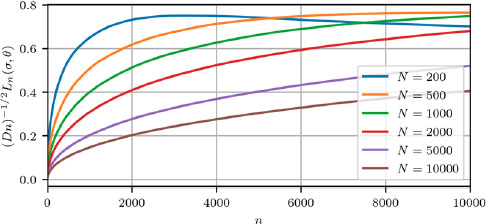
Figure 12.3. Maximum scaled regret versus step number c2 − c1 = 1. For a color version of this figure, see www.iste.co.uk/zafeiris/data1.zip
12.6. Conclusion
We reviewed a batch version of the UCB rule with a priori unknown control horizon.
An invariant description of the strategy was obtained.
Monte Carlo simulations were performed to study the normalized regret for different fairly large horizon sizes; it is shown that the maximum for regret is reached for n proportional to N, as expected based on obtained descriptions.
12.7. Affiliations
This study was funded by RFBR, project number 20-01-00062.
12.8. References
Garbar, S.V. (2020a). Invariant description for batch version of UCB strategy for multi-armed bandit. J. Phys. Conf. Ser., 1658, 012015.
Garbar, S.V. (2020b). Invariant description of UCB strategy for multi-armed bandits for batch processing scenario. Proceedings of the 24th International Conference on Circuits, Systems, Communications and Computers (CSCC), 75–78, Chania, Greece.
Kolnogorov, A.V. (2012). Parallel design of robust control in the stochastic environment (the two-armed bandit problem). Automation and Remote Control, 73, 689–701.
Kolnogorov, A.V. (2018). Gaussian two-armed bandit and optimization of batch data processing. Problems of Information Transmission, 54(1), 84–100.
Lai, T.L. (1987). Adaptive treatment allocation and the multi-armed bandit problem. Ann. Statist., 25, 1091–1114.
Lai, T.L., Levin, B., Robbins, H., Siegmund, D. (1980). Sequential medical trials (stopping rules/asymptotic optimality). Proc. Natl. Acad. Sci. USA, 77, 3135–3138.
Lattimore, T. and Szepesvari, C. (2020). Bandit Algorithms. Cambridge University Press, Cambridge, UK.
Vogel, W. (1960). An asymptotic minimax theorem for the two-armed bandit problem. Ann. Math. Statist., 31, 444–451.
Chapter written by Sergey GARBAR.
