16.2.1 Energy Storage

Until the past few years, electricity could not be stored at a large scale—the supply of electricity had to balance the demand at all times. More recently, however, grid‐scale energy storage has become technologically possible and financially practical. We can think of energy storage systems as large batteries, though other means for storing energy, such as flywheels, compressed air, and capacitors, are also being developed; see Akhil et al. (2013) for an in‐depth discussion. Some of these methods (e.g., capacitors) store electrical energy, while others (e.g., batteries) convert electricity to chemical or other forms of energy and then convert it back when needed.

Energy storage is playing an increasingly important role in modern electricity grids. For example, although renewable energy such as wind and solar provides cheap, environmentally friendly power, it is also unpredictable—the energy production changes stochastically as the wind speed changes or the cloud cover moves. This poses problems for an electricity system operator, which needs predictability in order to manage the grid efficiently. Moreover, wind power tends to be highest at night, while the demand for electricity is highest during the day. System operators can alleviate both the unpredictability and the timing mismatch using energy storage: The storage system is charged when energy is plentiful and discharged when the energy is needed to meet the demand.

In the near future, electricity consumers may use energy storage in their own homes. Home energy storage systems can be charged at night (when electricity rates are often lower) and discharged during the day to power the home's appliances and devices. Homes that have solar panels or other forms of renewable energy can use storage to buffer against the uncertainty from these sources, as discussed above. And energy storage can also be used to buffer against uncertainty in the home's demand for electricity. These systems may be standalone storage systems, or even the batteries of plug‐in hybrid electric vehicles (PHEVs) , when the energy is not fully needed for travel. This is sometimes referred to as “behind‐the‐meter” energy storage since it operates on the consumer's side of the electricity meter, rather than on the power grid side.

One can think of an energy storage system as an inventory system in which the product being stored is energy, rather than some physical item. Therefore, many of the models for managing energy storage are based on the fundamental inventory optimization models discussed earlier in this book. On the other hand, energy storage systems usually have more decisions to make; for example, in addition to deciding how much “inventory” to buy (as in classical inventory models), we might also choose how much to sell and at what price. In this section, we discuss two inventory‐like energy storage models: A behind‐the‐meter model for an electricity consumer and a model for a wind farm operator using storage to bid into an electricity market.

16.2.1.1 Behind‐the‐Meter Energy Storage

Consider a large‐scale battery located at a home (or an office building, university campus, etc.) that is capable of storing energy purchased from the grid. Energy that is stored in the battery can then be discharged, either to provide power for the devices in the home or to sell back to the grid. We will formulate an optimization model to decide how much energy to buy from and sell to the grid, and how much energy to charge and discharge the battery by, over a fixed planning horizon.

The amount of energy stored in the battery is called the state of charge and is expressed in units of kilowatt‐hours (kWh). The battery has a fixed capacity (in kWh). It is also common to assume there is a limit on how much energy (kWh) can be charged to or discharged from the battery per unit time, but for the sake of simplicity, we will ignore this constraint. Another important aspect of energy storage models is the energy losses that result from charging or discharging the battery, or even when storing energy over time, due to inefficiencies in the storage and energy conversion processes. We will ignore this aspect of the model too, but it is not difficult to include it.

We will assume that the time horizon is divided into discrete periods. The demand for energy in each period is random, with a known probability distribution. (It is straightforward to modify this model to handle uncertainty in other aspects of the system, such as electricity prices.) Although energy is being bought, sold, and used continuously throughout each period, and the demand uncertainty is being revealed continuously, we will assume instead that everything happens in discrete periods, with the following sequence of events:

1. We decide how much energy to purchase from or sell to the grid.
2. We observe the random demand.
3. We charge/discharge the battery to make up any discrepancy between the energy purchased and the demand. If the energy purchased plus the battery state of charge is insufficient to meet the demand, we incur an unmet‐demand penalty. If the demand plus the remaining battery capacity is insufficient to absorb all of the energy purchased from the grid, the extra energy is lost; there is no explicit penalty, except that we pay for the energy even though we don't use it.

Note that other sequences of events are possible. For example, we might learn the demand before making buy/sell and charge/discharge decisions, in which case we have more information available when we optimize. In practice, the grid and battery decisions are made in nearly continuous time, so any discrete‐time model is an approximation anyway. The sequence of events is a modeling decision and, as always, depends on a balance of realism and tractability.

Our goal is to maximize the expected profit (the expected revenue from selling energy minus the expected cost of purchasing it and the expected unmet‐demand penalty) over the horizon. (We will actually formulate the problem as minimizing the negative of the profit.) We will use the following notation:

Parameters
T	= number of time periods in horizon
	= price of energy, per kWh, when buying from grid in period t
	= price of energy, per kWh, when selling to grid in period t
	= penalty per kWh of unmet demand in period t
B	= capacity of battery, in kWh
	= initial state of charge, in kWh, in period 1
Random Variable
	= demand for energy, in kWh, in period t; is its realized value
Decision Variables
	= energy purchased from ( ) or sold to ( ) grid in period t
	= state of charge of battery at the end of period t

So, if , then we purchase kWh from the grid in period t, and if , then we sell kWh to the grid. In other words, is the energy purchased from the grid and is the energy sold to it.

Once has been chosen (step 1) and the actual demand has been observed (step 2), the battery charge/discharge quantity and the possible unmet demand are fully determined. In particular, if we know , the state of charge at the beginning of period t, then:

1. If : We charge kWh to the battery; there is no unmet demand.
2. If and : We discharge kWh from the battery; there is no unmet demand.
3. If : We discharge kWh from the battery; there is kWh of unmet demand.

We can combine these three cases to calculate the charge/discharge quantity and the unmet demand as follows:

(16.1)

(16.2)

(You should convince yourself that these equations correctly capture the logic described above.)

The problem of optimizing the buy/sell and charge/discharge decisions in this system and others like it can be modeled and solved as a multistage stochastic optimization problem ; see, e.g., Korpaas et al. (2003), Castronuovo and Lopes (2004), and Brown et al. (2008). Alternately, one can use Markov decision processes (MDP), also known as stochastic dynamic programming; see, e.g., Kim and Powell (2011), Harsha and Dahleh (2015), and Zhou et al. (2018). This is the approach we will take, and you will find it very similar to the approach used in Section 4.3.3 for inventory systems.

Let be the optimal total expected cost in period t through the end of the horizon, given that we start period t with a state of charge of x. Let be the terminal cost function : If there are x kWh in the battery at the end of period T, we incur a cost of . Then can be expressed recursively as follows:

(16.3)

The first two terms inside the are the grid purchase cost and sales revenue. The third term is the expected unmet‐demand penalty, using 16.2. The fourth term is the expected cost for the rest of the horizon, given that we start with a state of charge of x and then charge/discharge by , from 16.1.

The recursion 16.3 is very similar to (4.36), except that (1) the decision variable in the minimization is z, the power bought or sold, rather than y, the new inventory level; (2) power may be bought or sold, so there is no constraint such as , as in (4.36); and (3) the per‐unit coefficient c depends on whether we buy ( ) or sell ( ) power. It can be solved very similarly, using Algorithm 4.1 with suitable modifications.

16.2.1.2 Energy Storage for a Wind Farm Operator

Consider a wind farm operator that wishes to sell power to the electricity grid. Assume that there are two markets for buying and selling energy, a day‐ahead market and a real‐time market . (Many electricity systems around the world work this way.) In the day‐ahead market, firms bid by indicating how much electricity they are willing to provide during each time interval (say, each hour) in the next day, and at what prices. The system operator then determines which bids to accept, typically by solving a UC problem , and the firms whose bids are accepted are obligated to provide the electricity they committed to, at prices that are determined by the system operator based on the bids. In contrast, the real‐time market has no advance commitments; firms buy and sell electricity based on current prices, which change throughout the day.

Since wind power producers are typically small relative to the system as a whole, it is reasonable to assume that the wind farm operator has no control over the prices (the price component of its bid is irrelevant). Moreover, since wind is among the cheapest forms of electricity, we can also assume that bids from wind producers are always accepted. We will also make the simplifying assumption that tomorrow's day‐ahead prices are known deterministically.

Our wind farm operator wishes to decide how much to bid into the day‐ahead market for each hour tomorrow. The difficult issue here is that the wind power is stochastic, and moreover, if the firm cannot meet its bid during a given hour (because the actual wind power is insufficient), it must make up the difference in some other way, typically by buying power on the real‐time market. Real‐time prices are often lower than day‐ahead prices—so the firm may actually come out ahead in this case—but they sometimes spike much higher than day‐ahead prices, in which case the firm incurs significant costs. This problem is particularly acute for renewable energy producers, since the output of conventional energy generators can be controlled, while that of renewables is stochastic and largely out of the control of the operator.

In the models below, we will assume that the firm cannot sell to the real‐time market, though this assumption can be relaxed (see Problems 16.3 and 16.4).

Suppose first that the wind farm has no energy storage available. Therefore, the 24 hours in tomorrow's day‐ahead market are decoupled from each other, and we can solve each individually. Let Y be the wind power produced in a given hour; Y is a random variable with pdf and mean . Let c be the day‐ahead price for that hour, which we assume is deterministic, and let R be the real‐time price, which we assume is a random variable with pdf and mean . Our goal is to choose a value of Q, the bid quantity.

We can write the expected cost function as follows:

16.4

The first term represents the revenue, which we treat as a negative cost, while the second represents the expected cost of buying power from the real‐time market to make up any shortfall between the bid and the wind power produced. The second equality follows from the fact that Y and R are independent. The cost function in 16.5 is equivalent to the newsvendor cost function, plus a constant, and so can be solved easily; see Problem 16.2.

Now suppose that the wind farm has an energy storage system similar to that discussed in Section 16.2.1.1. The time periods are now coupled and must be solved simultaneously. We'll again use DP for this purpose, adding subscripts t to the notation defined above. Let be the optimal total expected cost in period t through the end of the horizon, given that we start period t with a state of charge of x, and let be the terminal cost function.

As in Section 16.2.1.1, once we choose the bid and observe the wind power in period t, the battery charge/discharge quantities are determined, as is the amount of electricity that must be purchased on the real‐time market. In particular, if is the state of charge at the beginning of period t, then:

1. If : We charge kWh to the battery and purchase no electricity from the real‐time market.
2. If and : We discharge kWh from the battery and purchase no electricity from the real‐time market.
3. If : We discharge kWh from the battery and purchase kWh from the real‐time market.

Therefore, the charge/discharge quantity and the quantity purchased from the real‐time market are as follows:

(16.5)

(16.6)

Then the recursion for is given by:

(16.7)

The first term inside the is the revenue from selling power on the day‐ahead market, while the second is the expected cost of buying power on the real‐time market, from 16.6. The third term is the expected cost for the rest of the horizon, given that we start with a state of charge of x and then charge/discharge by , from 16.5. Once again, the recursion is very similar to the inventory recursion (4.36) and can be solved using a modification of Algorithm 4.1.

16.2.2 Transmission Capacity Planning

Wind farms are often located in geographical areas with low population density, far from major load (demand) centers, and cannot be directly integrated into the existing electricity transmission network. As a result, long‐distance transmission lines must be constructed to deliver electrical power from remote wind farms. In this section, we discuss a model for optimizing the capacity of such a transmission line. Our model is based on the work of Qi et al. (2015), though they model and solve the problem directly, whereas we will treat it as a newsvendor problem.

Suppose that a planner wishes to decide the capacity of the transmission line that connects a remote wind farm to the existing power grid. The system operator has implemented a feed‐in tariff policy, a multiyear contract in which the wind farm is paid c per kWh transmitted to the grid, regardless of the quantity. Thus, the price is independent of quantity, as in Section 16.2.1.2, but unlike in that section, here the wind farm operator does not need to commit to a generation quantity in advance.

The wind farm is equipped with an energy storage system (battery) like that discussed in Section 16.2.1.2. We assume that the battery has effectively infinite capacity. Because of this, and because the feed‐in tariff means there is no incentive to use storage to take advantage of price changes over time, we can ignore many of the details we modeled in Section 16.2.1.2.

Intuitively, the trade‐off faced by the transmission line planner is that as the line capacity increases, so does the construction cost, but the energy losses decrease. The energy loss is due to the dissipation in energy due to friction as the battery is charged and discharged. (We ignored these energy losses in earlier sections.)

To quantify this trade‐off, denote the transmission line capacity S kW. The annualized cost to build the transmission line is linear in the capacity, given by KS, where is the cost per kW of capacity. ¹ Let the charge and discharge efficiency of the battery be , respectively. In other words, if 1 kWh of energy is charged to the battery, the battery actually “receives” kWh, and if 1 kWh is discharged from the battery, the transmission line actually “receives” kWh from the battery. Thus, if we charge 1 kWh and subsequently discharge it, the net energy received from this “round trip” is . The kWh of energy that are lost to friction represent lost revenue. A larger transmission line capacity might have avoided this lost revenue, but would of course have cost more.

We can model this decision as a newsvendor problem. As in Section 16.2.1.2, let Y be a random variable that equals the wind power generated in one hour. For each kWh of difference between the wind power generated, Y, and the line capacity, S, we incur either a holding (overage) or stockout (underage) cost.

In particular, suppose the capacity is greater than the wind power in a given hour ( ). If we had built one fewer kW of capacity, we would have saved in this hour, where converts the construction cost from years to hours. Therefore, the holding cost, the cost of building too much transmission capacity, is .

Now suppose instead that the capacity falls short of the wind energy ( ). The surplus energy is charged into the battery and then discharged at some future time. Each kWh of surplus energy results in an energy loss of and a revenue loss of . On the other hand, each kWh of surplus energy saved us in transmission line construction costs for this hour. Therefore, the stockout cost, the cost of building too little transmission capacity, is .

Let be the cdf of Y, and let and be its mean and variance. Then, from (4.16), the optimal capacity, , solves

(16.8)

If Y has a normal distribution, we can use (4.24) to get an explicit expression for . However, wind power is often modeled using the Weibull distribution, typically with parameters that do not follow and therefore are not conducive to approximating it with the normal distribution.

Instead, we can approximate the wind power distribution as , which has been shown numerically to provide a good fit (Qi et al., 2015). The cdf of a random variable is . Therefore, 16.8 becomes

However, the transmission line capacity must be greater than or equal to the mean wind power, , otherwise the battery storage level will increase to infinity over time. Therefore, we have

where

The constant captures the trade‐off between the transmission capacity and the storage efficiency. If K is large—say, because the transmission line is long, or because construction is very expensive—or if the battery is efficient so that , then will be close to 1, and it will not be cost‐effective to invest in extra transmission capacity (over and above ).

16.2.3 Electricity Network Design

Electricity networks are fundamentally different from supply chain networks. In supply chain or other transportation networks, we can decide how much flow to send on each arc in the network (subject to capacity constraints). However, in electricity networks, it is the laws of physics, rather than our own decisions, that dictate these flows. We can decide how much electricity to inject into the network at generator nodes and how much to withdraw from the network at demand nodes, but after those decisions are made, the flows are determined by Kirchhoff's laws . One way to think about this difference is that in supply chain networks, we can control quantities on arcs, whereas in electricity networks, we can only control quantities at nodes. This makes designing and operating electricity networks more mathematically complex than doing the same for supply chain networks.

For a simple example, see the network in Figure 16.1. The node on the left supplies 150 units, while the node on the right demands 150 units. The upper and lower arcs have a capacities of 100 and 50, respectively, but are identical in all other respects. In a supply chain network, we can simply ship 100 units on the upper arc (road) and 50 on the lower. But in an electricity network, since the two arcs (power lines) have identical characteristics, 75 units will flow on each line, violating the capacity of the lower one.

In this section, we discuss a model for constructing a new electricity network. The model is based on the arc design model in Section 8.7.2 but accounts for the electricity flows. Many electricity network design models assume that a portion of the network has already been constructed, and we are deciding which additional links to add—they are network expansion rather than network design models—but we will omit this extra complication and assume that we are designing the network from scratch. It is straightforward to modify the model to account for existing links.

The terminology of electricity grid analysis differs somewhat from that of supply chain networks. Nodes are known as buses, and arcs or edges are known as lines. Let N be the set of buses and E be the set of potential lines. Demands are called loads, and demand buses are load buses. Each bus i has a voltage . Voltages are represented by complex numbers , and the relationship between power flows and voltages is nonlinear and nonconvex. However, we will instead consider the so‐called linearized or DC power flow model, which ignores the imaginary component of the complex voltage and focuses instead on the so‐called real power.

Bus i is assigned a voltage angle . The line between buses i and j (called line ) has a susceptance ; very roughly speaking, when the susceptance is larger, power flows more easily through the line. In particular, the power that flows on line is given by

(16.9)

If , then power is flowing from i to j, and vice versa. Bus i's total power is given by

(16.10)

if , then power is flowing out of bus i, and vice versa. The power at bus i is bounded above and below:

(16.11)

if i is a load bus, then (and both are negative). Finally, the power flowing on line is bounded by the line capacity, denoted :

(16.12

Constraints 16.9–16.12 constitute the DC power flow model. The OPF problem discussed above has an objective function of minimizing the total generation cost and has 16.9–16.12 as constraints. But our interest is in using 16.9–16.12 to model the power flows in the network design problem.

To that end, let be the fixed cost to construct line , and let if we construct the line and 0 otherwise. The other decision variables in the model are , , and . Then the electricity network design problem is:

(16.13)

(16.14)

(16.15)

(16.16)

(16.17)

(16.18)

Constraints 16.14–16.17 are the power flow constraints, modified to account for the construction variables . In 16.14, M is a large constant. If , then we construct line , and 16.14 is equivalent to 16.9; otherwise, the constraint has no effect. This constraint is nonlinear because of the absolute value, but it can be linearized using standard methods. Similarly, if , then 16.17 bounds the power flow on line by the capacity, whereas if , then is forced equal to 0. Finally, constraints 16.18 are integrality constraints. Note that is unrestricted in sign.

Electricity network design problems can be solved using various MIP optimization techniques such as Benders decomposition (Oliveira et al., 1995; Binato et al., 2001), dynamic programming (Dusonchet and El‐Abiad, 1973), or metaheuristics (Romero et al., 1995), or using off‐the‐shelf solvers (Alguacil et al., 2003).

16.3.1 Production Planning and Contracting for Influenza Vaccines

Influenza (flu) is a respiratory illness that spreads easily from person to person. Each year, millions of people worldwide get seriously ill with influenza, and hundreds of thousands die from the disease (World Health Organization, 2018). Vaccination is the most effective means for controlling the disease.

Influenza vaccines can be thought of as newsvendor‐type products, with a single selling season. This is because the strains of the influenza virus that are included in the vaccine change each year, based on analysis by the World Health Organization (WHO) of the virus strains that are most prevalent at the time. Therefore, last year's vaccines cannot be used this year. Vaccines that are administered year‐round without seasonal effects, such as childhood vaccines for polio, measles, and the like, are also perishable (they have expiration dates). But their compositions do not change annually, and their shelf lives are typically longer than their ordering cycles. Therefore, their inventories can be managed using modified EOQ‐type models.

On the other hand, the influenza vaccine has two key differences from the classical newsvendor assumptions: yield uncertainty and nonlinear sale value. Yield uncertainty (Section 9.3) arises from the fact that the yield attained from the manufacturing process—which takes place largely inside embryonated chicken eggs —is difficult to predict and depends significantly on the virus strains that are included in the vaccine. The nonlinear sale value is a result of the epidemiology of the flu, namely, that the incremental benefit of one additional person vaccinated depends on the number of people who have already been vaccinated—it is not a constant.

Chick et al. (2008) introduce a model for the Stackelberg game that occurs when a large buyer (e.g., a government) purchases vaccines from a supplier. We present a simplified version of their model here.

In this Stackelberg game, the buyer (the government) is the leader and the supplier is the follower. (Note that this is the opposite of the sequence considered in the Stackelberg models in Chapter 14.) The government wishes to purchase enough vaccine to vaccinate a fraction f of its population of N individuals; the government's decision variable is f. Each individual to be vaccinated requires doses of the vaccine. Therefore, the government's total demand is .

The supplier then decides how many eggs to inject with the virus, Q. The number of vaccine doses produced is given by the multiplicative yield QZ, where Z is a random variable with pdf . Each egg injected costs the supplier . The government pays w to the supplier for each dose it purchases, and it also incurs a cost of per individual vaccinated. Finally, there is a cost of b per infected individual, which can include treatment costs, lost wages, etc. Although b is a societal cost, we will assume it is borne by the government.

If we vaccinate a fraction f of the N individuals in the population, then the function measures the expected number of individuals that will have been infected by the end of the influenza season. can be calculated using epidemiological models; in this case, we use a standard model called the SIR model, where the acronym stands for the three “compartments” of individuals: susceptible, infectious, and recovered (Anderson and May, 1992). Susceptible individuals are vulnerable to becoming infected with the disease; infectious individuals have the disease and can communicate it to others; and recovered individuals are no longer infectious (or were immune to begin with). Under standard assumptions, we get that , where p, the “attack rate,” satisfies

(16.19)

and are the initial numbers of susceptible and infectious individuals at the start of the season, and is the “basic reproduction number,” i.e., the number of new cases generated by each new case, on average. For influenza, is roughly 2–3.

The function is plotted in Figure 16.2. Clearly, it is nonlinear. This function indicates the value that the government gets as a function of its decision variable, which is why the problem has a nonlinear sale value, unlike the classical newsvendor problem. The nonlinearity itself is not necessarily a major impediment for the newsvendor problem, but the fact that p must be characterized implicitly (it appears on both the left‐ and right‐hand sides of 16.19) is.

On the other hand, can be approximated well by a simple piecewise‐linear function, also plotted in Figure 16.2. The breakpoint occurs at , where is the “critical vaccination fraction,” i.e., the smallest value of f that brings down to 1. The value of is straightforward to calculate in the SIR model.

Let's first look at the supplier's problem. Since the government acts first, the supplier already knows that the government's demand is . It faces multiplicative yield uncertainty in a newsvendor‐type setting. The actual number of doses produced, QZ, may be greater than, less than, or equal to . Each dose of vaccine that is produced but not used incurs a cost of , whereas each unit of unmet demand incurs a cost of . (This is the supplier's stockout cost—the government's, and the population's, cost of vaccine shortages is quite different.)

The supplier's expected cost function is given by

(16.20)

The first term represents the cost of injecting Q eggs. The second represents the sales revenue, since the supplier sells the government either the number of doses produced or the government's order quantity, whichever is smaller. One can rewrite as

(16.21)

(See Problem 16.5.) Compare 16.21 to the single‐period newsvendor problem with deterministic demand and multiplicative yield uncertainty in Section 9.3.2.3. The last two terms are equivalent to (9.30) with (because each dose of the vaccine that is produced but not used incurs a cost of ), (for each unit of unmet demand, the supplier incurs a lost profit of ), and . However, by setting , we are implicitly assuming that we only pay for units that are produced. But the supplier in the vaccine model pays for every egg used, whether or not it yields a dose of vaccine. Therefore, we must add the expected cost of the eggs that are injected but do not yield vaccine doses; this is the first term in 16.21. Finally, the second term is similar to the additive constant that converts between the explicit and implicit versions of the newsvendor cost function; see Section 4.3.2.4 and Problem 4.15.

From (9.31), we get

Therefore, for a given f, the optimal quantity satisfies

Now consider the government's problem. The government wishes to choose f to minimize the total expected cost of infections and of purchasing and administering vaccines:

(16.22)

where

U is the number of vaccine doses purchased: the minimum of the production yield and the number ordered. V is the number of doses administered: If the number purchased is less than , we only administer , because administering more doses is not cost‐effective. (We omit the justification for this latter claim; see Chick et al. (2008).) The three terms in 16.22 represent the expected costs of infections, vaccine purchases, and vaccine administration, respectively. When the government chooses f, it knows that the supplier will choose , so it can replace Q with in 16.22.

The arrangement described above is a wholesale price contract . The supplier's optimal production quantity, , under this contract is smaller than the system‐optimal quantity , i.e., the quantity that a centralized decision‐maker would choose in order to minimize the total cost system‐wide cost. Therefore, the supply chain is not coordinated. The under‐production occurs because the supplier bears all of the risk of arising from the yield uncertainty.

Chick et al. (2008) introduce a contract called a cost‐sharing contract in which the government pays the supplier an additional cost per egg injected, in addition to the cost that it pays per vaccine dose delivered. The government therefore assumes some of the risk of excess production, inducing the supplier to increase its production quantity. If the contract parameters are set appropriately, the new production quantity is system‐optimal, and the supply chain is coordinated.

16.3.2 Inventory Management for Blood Platelets

Blood platelets are used during many types of surgeries and are part of the treatment regimen for patients with leukemia and other cancers, as well as for a wide range of other medical conditions. The management of the inventory of platelets is particularly difficult because (1) platelets are usually in short supply, since donating platelets is much more time‐consuming than regular blood donations; (2) demand for platelets is random and nonstationary, e.g., with less demand on weekends; and, most importantly for our purposes, (3) platelets are highly perishable. Platelets have a shelf life of only 5 days from the time of donation; and since the first 2 days are taken up by transportation, testing, and processing, the shelf life is really only 3 days once the platelets reach a hospital.

Most hospitals order platelets from blood banks every 1–2 days. If they only ordered every 3 days, the inventory problem would be easy—it would be equivalent to an infinite‐horizon newsvendor problem, since the inventory in each replenishment order expires just before the next order is placed. But the fact that the order interval is shorter than the shelf life complicates the analysis.

As a starting point, consider the periodic‐review models of Section 4.3. The infinite‐horizon model (Section 4.3.4) is not appropriate here because it assumes the demands are stationary. Therefore, the finite‐horizon model (Section 4.3.3) will be the basis for our platelet model.

First consider a generic model for a product that has a shelf life of m periods: Items that arrive in period t expire at the end of period . (So, for the newsvendor problem, .) All inventory arrives new, and inventory is used according to a first‐in, first‐out (FIFO) policy, i.e., oldest first. This model was introduced by Nahmias (1975).

We'll consider the lost sales case, which makes the accounting a bit easier, but the model can be modified for backorders if desired. In addition to the usual per‐unit ordering, holding, and stockout costs, there is a cost of b per item that expires, called the outdate cost. We will use the same sequence of events as in Section 4.3. With the nonstationarity of platelet use in mind, one could also allow the demand distribution to vary over time, with representing the pdf of the demand in period t, though we will assume stationarity to keep things simpler.

Let be the inventory on hand at the beginning of a given period that will expire in exactly i periods (we call these “type‐i” units), and let be the corresponding vector. Thus, the inventory vector at the start of period t is , then units will expire at the end of period t, will expire at the end of , and so on. To formulate the DP recursion, we will need to know the starting inventory vector for period , given , the order‐up‐to quantity y, and the demand d. This vector is given by a (vector‐valued) function denoted , which is characterized in the next lemma. That lemma also identifies the number of units that expire in each period, which we need in order to calculate the outdate cost.

We interpret (which occurs when in parts (a) and (b)) as the number of units that were ordered in period t, i.e., . These “fresh” units will expire at the end of period . In part (a), if , then the sum is taken to equal 0.

Note that if , then Lemma 16.1(b) just says that the number of stockouts in period t is , as usual. Similarly, the period‐t ending inventory is simply , as usual. In other words, the function from (4.37) still gives the expected holding and stockout cost. By Lemma 16.1(a), the expected outdate cost is

Let be the optimal total expected cost in periods if we start period t with inventory vector . Then, using the ideas in Section 4.3 and Lemma 16.1, we can express recursively as

(16.23)

(As usual, x represents the starting inventory, i.e., .)

Equation 16.23 seems familiar, with a few new twists, most notably the use of the function to relate the ending inventory in period t to the starting inventory in period . Moreover, Nahmias (1975) proves that the function inside the in 16.24 is convex in y (although, unlike in the model in Section 4.3, is not convex in !). Therefore, the form of the optimal policy can be characterized (see Nahmias (1975)), though its structure can be quite complex.

This should all be good news. Unfortunately, however, things are not so simple, because of the curse of dimensionality: The size of the state space explodes rapidly with m, since the state space has dimension . For example, fresh milk has a shelf life at the grocery store of roughly 2 weeks. If the grocery store never orders more than, say, a dozen cartons of milk per day (i.e., ), then the state space has elements! And for each possible state, we need to solve the minimization problem in 16.24, and we need to do this for every period in the time horizon.

For this reason, the model above, introduced in 1975, is not often implemented in practice. Some simpler settings have been considered: For example, Nahmias and Pierskalla (1973) consider , which means the state variable has only one dimension. Heuristics have also been developed for the m‐period problem (Nandakumar and Morton, 1993). And of course, if , then we simply have a newsvendor problem.

All of which brings us back to blood platelets. Since platelets have a shelf life of 3 days, we have a reasonable value of m, making Nahmias's (1975) model practical. Zhou et al. (2011) study the inventory of platelets specifically, assuming that the hospital places “regular” replenishment orders for platelets every 2 days but can also place “emergency” orders on the off‐days. They use this model to provide guidance to hospitals about whether they should order every day or every 2 days, based on the demand and cost parameters. See also Prastacos (1984) for a review of OR models for blood inventory management.

16.4.1 Disaster Relief Routing

After a natural or manmade disaster, it is critical to distribute emergency supplies to affected people quickly and efficiently. The supply chain that enables this distribution is usually established, at least in part, in real time immediately following the disaster. Further complicating the planning process are logistical complications such as limited resources, damaged roads, and multiple agencies coordinating (sometimes poorly) to provide relief.

Figure 16.3 depicts a typical disaster‐relief supply chain. Supplies arrive in the affected country from around the world via a port of entry, from which they are shipped to a central warehouse. From there, supplies are shipped to local distribution centers (LDCs), which are often established in makeshift locations such as schools or warehouses, or even temporary facilities such as tents. Deliveries are made from LDCs to the recipients of emergency aid via less‐than‐truckload (LTL) shipments consisting of multiple stops per route. This last portion of the supply chain is referred to as last‐mile distribution.

Balcik et al. (2008) introduce a model for last‐mile disaster relief distribution. Their model considers both resource allocation (how many supplies to deliver to each demand node, and when) and vehicle routing (how to route the delivery vehicles to the demand nodes). Because of the resource allocation component, their model resembles the inventory–routing problem (IRP) from Section 12.4 more closely than the vehicle routing problem (VRP) from Chapter 11. However, unlike the IRP formulation in Section 12.4, which makes yes/no decisions for individual edges of the network in order to construct the routes, the model by Balcik et al. (2008) assumes the potential routes have already been identified, and it selects routes from among them. This is especially practical in developing countries in which the road network is not highly connected, so that the total number of potential routes is not large (VonAchen et al., 2016).

Assume that a set of demand nodes has already been assigned to each LDC, so that we can solve the problem for each LDC separately. The model considers a finite planning horizon, during which we may make one or more deliveries to each demand node. Emergency supplies are often categorized as either Type 1 items such as tarps and blankets, which are delivered once at the beginning of the horizon, or Type 2 items such as food and water, which are consumed and therefore must be delivered throughout the horizon. Balcik et al. (2008) consider both types of supplies in their model, but for the sake of simplicity, we will consider only Type 2 items. We will consider a single product, which is used to model all Type 2 items in aggregate.

In disaster relief supply chains, there is an insistence on equity in resource allocation and a priority placed on serving vulnerable groups. In this model, unmet demands are assumed to be lost, rather than backordered, but the stockout penalty is based on the maximum weighted unmet demand fraction among all demand nodes. Thus, it is considered preferable for every node to have 10% of its demands unmet than for one node to have 20% of its demands unmet and every other node to have all of its demands satisfied. This type of objective would be unusual in commercial supply chains, which are typically driven by cost or revenue, not equity. Moreover, the model allows some nodes to be weighted more than others when calculating the maximum unmet demand fraction, so that priority may be placed on, for example, vulnerable populations. (See Huang et al. (2012) for further discussion of equity in disaster relief routing.)

A second characteristic of disaster relief distribution problems that differs from commercial supply chains is the inherent uncertainty in demands, supplies, and even the duration of the planning horizon itself. Rather than modeling this uncertainty explicitly using scenarios (as in Section 8.6), Balcik et al. (2008) propose a rolling‐horizon approach in which we solve the model for a finite horizon, implement the solution for the first period, then update the estimates of the uncertain parameters, shift the horizon by one period, and solve the model again.

Another difference between relief and commercial supply chains is that in a disaster, it is not always possible to use larger, more cost‐effective trucks to deliver all supplies, since those trucks may not be able to travel on certain roads that have been damaged by the disaster. To model this, we assume that each vehicle in the fleet has its own capacity, speed, and ability to travel on each link.

The model assumes that all possible clusters of demand nodes have been enumerated, and for each cluster, a traveling salesman problem (TSP) has been solved to determine the shortest route through those nodes beginning and ending at the LDC. (Of course, this is only practical if the number of demand nodes is reasonably small; otherwise, heuristics can be used to identify good clusters, and good routes for each.) The resulting list of routes is an input to the model. We assume that each vehicle can complete multiple routes in one period, and each demand node can be visited multiple times in one period. Each route is included in the list multiple times, once for each time it can be traveled in one period. For example, if one period is 24 hours long, then a 15‐hour route is included once, but a 10‐hour route is included twice.

The costs of the model include transportation costs from the LDC to demand nodes, as well as a stockout cost for unmet demand (which is assumed to be lost rather than backordered). Excess inventory can be held at a demand point from one period to another, but the holding cost is assumed to be negligible compared to the other costs and is therefore ignored.

We use the following notation:

Sets
I	= set of demand nodes
K	= set of available vehicles
R	= set of routes
	= set of demand nodes included on route
T	= set of time periods
Parameters
Costs
	= cost of route for vehicle
	= stockout weight at node in period
Other
	= demand of node in period
	= supply delivered to LDC at the beginning of period
	= capacity of vehicle
	= fraction of one period that route requires when using vehicle
Decision Variables
	= 1 if route is traveled by vehicle in period , 0 otherwise
	= amount of supplies delivered to node by vehicle via route
	in period
	= stockout penalty in period
	= fraction of demand at node that is unsatisfied in period
	= on‐hand inventory at location at the beginning of period

The relief routing problem can then be formulated as follows:

(16.24)

(16.25)

(16.26)

(16.27)

(16.28)

(16.29)

(16.30)

(16.31)

(16.32)

The objective function 16.24 calculates the total transportation and stockout cost. Constraints 16.25 enforce the available supply at the LDC in every time period: The total amount shipped to every demand node by every vehicle on every route in every period up through time t cannot exceed the total supply delivered to the LDC up through time t. Constraints 16.26 set the stockout penalty in period t, , equal to the maximum of the weighted stockout fraction over all nodes in period t. Note that is a fraction, but can be scaled up or down to convert the stockouts to an equivalent value in currency so that it can be added to the objective function.

The quantity inside the parentheses in constraints 16.27 is equal to the unmet demand at node i in period t: It equals the demand minus the starting inventory and arriving shipments, adding back any units that are reserved for period . Constraints 16.27 therefore set equal to the fraction of node i's demand that is unmet in period t.

Constraints 16.28 enforce the vehicle capacity, while constraints 16.29 ensure that the routes traveled by vehicle k in a given period do not exceed the period length. Constraints 16.30–16.32 are nonnegativity and integrality constraints.

Balcik et al. (2008) solve the model using an off‐the‐shelf MIP solver. Even for small instances, though, the model takes a few hours to solve.

16.4.2 Passenger Screening

Consider an aviation security agency, such as the United States Transportation Security Administration (TSA), that wishes to determine which security classes to assign passengers to. A class consists of the equipment (such as metal detectors) and procedures (such as manual baggage inspections) that will be used to screen passengers assigned to that class. Each class that is selected for use involves a fixed cost to purchase the equipment, train the security agents, and so on, as well as a per‐unit cost for each passenger assigned to that class.

For example, one class might consist of screening the passenger using a metal detector, screening the passenger's carry‐on baggage using an x‐ray machine, and screening his or her checked bags using an explosive detection system (EDS). Another class might consist of the same three screenings, plus a hand‐wand inspection for the passenger and a detailed hand search of the carry‐on baggage. A third class might consist of the same as the first class plus an open‐bag trace (in which the bag is tested for traces of explosive‐related chemicals using a swab) for the carry‐on baggage and an open‐bag trace plus a detailed hand search for the checked baggage. The agency may choose to employ some or all of these classes but can only assign passengers to a class that has been chosen. There is a fixed cost for each class chosen, which implicitly assumes that each class has its own dedicated equipment; if two classes each use an EDS, for example, they must each have their own dedicated EDS equipment.

Assume that the agency knows the number of passengers traveling through a given airport at a typical peak hour, as well as the assessed threat level of each passenger. (How these threat levels are assessed is a highly sensitive subject, and rife with controversy, but is outside the scope of our discussion.) The agency's goal is to decide which security classes to use, and which passengers to assign to each class, in order to maximize the security provided while respecting a budget constraint.

In this section, we will formulate a discrete optimization model to solve this problem. The model was introduced by McLay et al. (2006). This and other related papers provided the analysis that laid the groundwork for the TSA's PreCheck program (McLay, 2015).

Let I be the set of passengers in a typical hour and let J be the set of potential security classes. Let be the assessed threat level of passenger i, and let be the security level achieved by class j. If passenger i is assigned to class j, the resulting security level is calculated as , and our goal is to maximize the sum of this value over all passengers. Therefore, the objective encourages passengers with high assessed threat levels to be assigned to classes with high security levels.

The fixed cost for security class j is denoted by , and the per‐passenger cost is . The fixed cost includes the initial investment cost, divided by the total number of hours in the equipment's expected useful life, plus the hourly cost to operate the equipment. The agency has a fixed budget of b available to spend on these costs per hour.

There are two sets of decision variables in the model:

	= 1 if class j is chosen, 0 otherwise
	= 1 if passenger i is assigned to class j, 0 otherwise

(16.33)

(16.34)

(16.35)

(16.36)

(16.37)

The objective function 16.33 maximizes the total security level. Constraints 16.34 require every passenger to be assigned to a class, and constraints 16.35 prevent a passenger from being assigned to a class that has not been chosen. Constraint 16.36 is the budget constraint. Constraints 16.37 are integrality constraints.

This model is very similar to the uncapacitated fixed‐charge location problem (UFLP) from Section 8.2. The main differences are that the total cost is bounded in the constraints, rather than minimized in the objective, and that the objective instead maximizes the security. The per‐unit cost is also slightly different, since it depends only on the screening class and not on the passenger; that is, it is written instead of . Moreover, there is no term, as in the UFLP, because the passengers are assumed to be enumerated in the set I. We could instead define I as the set of passenger types, in which case might represent the number of passengers of each type, and we would multiply the objective function 16.33 and the per‐unit cost in 16.36 by .

On the other hand, the presence of the budget constraint 16.36 makes this problem harder to solve than the UFLP. McLay et al. (2006) propose a greedy heuristic to solve the problem, as well as a dynamic programming (DP) algorithm that can be used when the number of classes is relatively small.

The model above is static, in the sense that it considers a single time period and assumes that passenger threat levels are known. In contrast, dynamic screening models assume a sequential process in which a passenger's threat level is not determined until she or he reaches a security checkpoint. McLay et al. (2009,2010) and Nikolaev et al. (2007) formulate such models as MDPs.

16.4.3 Public Housing Location

Public housing authorities (PHAs) provide affordable housing for low‐income residents of a city or other area. For many years, the predominant strategy used by PHAs in large cities in the United States was to build large, high‐rise housing developments. Such developments were cheaper to build and maintain due to economies of scale, but they gained a reputation for fostering crime and gang violence, as well as leading to increased racial and socio‐economic segregation. More recently, U.S. PHAs have favored lower‐density housing projects that are spread more widely throughout the city.

Although PHAs have not typically used OR methods for decision‐making, the problem of deciding where to locate public housing throughout a city is a natural facility location problem. It is made more complicated by the fact that the decision involves multiple stakeholders with competing objectives: The PHA might want fewer, larger projects; the residents want locations that offer good schools and other benefits; society as a whole wants integrated, diverse communities; while at the same time, many neighbors of potential housing projects do not want the project to be built at all. The political forces, social controversy, and moral questions surrounding public housing are very difficult to quantify, but once an attempt has been made to do so, OR can offer tools to help navigate these issues in choosing project locations.

Johnson (2006) introduces a multiobjective facility location model to choose where to locate public subsidized housing projects and how many housing units to build at each location. The first objective is the economic efficiency, defined as the difference between the costs of constructing the facilities and the economic benefits accrued by the residents, the neighboring community, and society as a whole. (The costs may be straightforward to measure, but the benefits, of course, are not. They also tend to be nonlinear, but we will treat them as linear.) The second objective is the perceived equity among the various stakeholders—another metric that is difficult to quantify and that is typically nonlinear. Johnson (2006) proposes, as a proxy, a dispersion objective, i.e., maximizing the distances among the projects located. (See Section 8.5.1.)

Let J be the set of potential locations for the housing projects, and let be the distance between locations j and k in J. Let be the fixed cost to build a project at location j, and let be the net economic benefit for each unit built there. (That is, is the benefit accruing from one unit of housing built in a project at location j minus the cost of building the unit.) Assume that the PHA wishes to build a total of H units, and that at most units can be built at location j.

The model uses decision variables , which equals 1 if we build a project at location , 0 otherwise; and , which is the number of units to build at location j. It also uses a set of auxiliary variables , which equals if we build projects at both locations j and k, and equals a large number otherwise.

Johnson (2006) formulates the public housing location problem as follows:

(16.38)

(16.39)

(16.40)

(16.41)

(16.42)

(16.43)

(16.44)

The model contains two objective functions. The first 16.38 calculates the economic efficiency of the projects and units that are built. The second 16.39 maximizes the minimum distance between any two housing projects. By constraints 16.40, if , and equals a large number otherwise. (M is a large constant.) Thus, if or equals 0, has no effect in 16.39. Constraint 16.41 ensures that exactly H units will be built. Constraints 16.42 enforce the capacity‐type restriction that no more than units can be built at location j if a project is located there ( ) and prevents any units from being built there if . Constraints 16.43 and 16.44 are integrality and nonnegativity constraints.

To transform this model into a single‐objective model that can be solved using an off‐the‐shelf MIP solver, Johnson (2006) proposes using the weighting method (Cohon, 1978), in which the two objectives are combined into a single objective function by taking a linear combination of them. (We discussed a similar approach in Section 9.6.5.) By varying the weight systematically, we obtain a trade‐off curve.

This model is NP‐hard and is much more difficult to solve, computationally, than many other NP‐hard facility location problems such as the UFLP (Section 8.2). Johnson (2006) reports CPLEX computation times of 4 hours or more for a case study with . That case study uses economic data for Cook County, Illinois to explore the model and its outcomes. The resulting trade‐off curve, unfortunately, does not contain as many points as the curve in Figure 9.11, meaning that decision‐makers have less flexibility in navigating the competing objectives. It also does not have as sharp an “elbow,” i.e., it requires more of a sacrifice in one objective in order to improve the other. Nevertheless, the model is still valuable as a planning tool and can allow PHAs to make data‐driven decisions in a flexible and equitable framework.

1. 16.1 (Single‐Period Behind‐the‐Meter Problem) Show that the behind‐the‐meter energy storage problem from Section 16.2.1.1 is equivalent to a newsvendor problem (possibly plus a constant) if .
2. 16.2 (Single‐Period Wind Farm Problem) Show that the expected cost function 16.5 is equivalent to a newsvendor problem (possibly plus a constant) by giving values for h and p, in terms of the notation in Section 16.2.1.2, that make the two cost functions equal (except for an additive constant). What is the optimal bid quantity?
3. 16.3 (Selling on the Real‐Time Market) Modify the single‐period wind farm problem from Section 16.2.1.2 to allow the wind farm operator to sell power to the real‐time market if the observed wind power is greater than its bid on the day‐ahead market. Is the problem still equivalent to a newsvendor problem? If so, what is the optimal solution?
4. 16.4 (Multi‐Period Selling on the Real‐Time Market) Modify the recursion 16.7 to allow the wind farm operator to sell power to the real‐time market in each period if it wishes.
5. 16.5 (Vaccine Supplier's Expected Cost Function) Prove that 16.21 equals 16.20.
6. 16.6 (System‐Optimal Solution for Vaccine Problem) In the vaccine model in Section 16.3.1, suppose that the function is approximated using the following piecewise‐linear function:
   (16.52)

   where M and are nonnegative constants. (This is the function plotted in Figure 16.2.) Assume that (so that the expected benefit from vaccination exceeds the cost).

   1. Prove that the system objective function (i.e., ) is given by
      

      where

      

      Now, let be the solution that minimizes .

   2. Prove that all values of in are optimal for the system.
   3. Prove that satisfies
      
7. 16.7 (Shared Security Equipment) The passenger screening model in Section 16.4.2 assumes that each security class uses its own dedicated equipment. Relax this assumption by assuming that there is a set of equipment types and that each security class uses a predefined subset of those types. The fixed and per‐unit costs apply to the equipment, rather than to the classes. Formulate a model that decides what equipment to purchase and which classes to assign each passenger to, in order to maximize the total security, while respecting a budget constraint. You will have to introduce new notation; define it clearly. Explain your objective function and constraints in words.
8. 16.8 (Integral Number of Housing Units) In the public housing location problem in Section 16.4.3, we defined 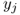, the number of housing units to build at location j, as a continuous decision variable. Does there always exist an optimal solution to this model in which will be a nonnegative integer? Justify your answer.