Chapter 15
Auctions
15.1 Introduction
Auctions have been around for centuries and the mathematical analysis of auctions dates back decades. But they have enjoyed growing popularity in recent years because the Internet has made efficient implementation of auctions, even complex ones, possible. Consumer auctions like eBay have become household names, but business‐to‐business (B2B) auctions have grown even more quickly. B2B auctions are mainly procurement auctions in which there is a single buyer and multiple sellers (the reverse of most consumer auctions; in fact, such auctions are called reverse auctions). For example, auto manufacturers have set up auctions in which thousands of potential suppliers bid for contracts; the auto company chooses the suppliers with the lowest prices. Clearly, such an undertaking would be much more cumbersome without the Internet. We will consider auctions with a single seller and multiple potential buyers.
There are many types of auctions, each with various properties in terms of consumer behavior, efficiency, and so on. Here are just a few types of auctions that have been introduced in the literature and in practice:
- English: Perhaps the most familiar type, with each bidder publicly announcing his bid and the price rising until only a single bidder remains. The highest bidder wins and pays his bid.
- Sealed‐bid first price: Bids are made privately and simultaneously by all bidders. The bidder with the highest bid wins and pays his bid.
- Sealed‐bid second price: Sometimes known as a Vickrey auction, this auction type is like the sealed‐bid first price auction except that the winner pays the second‐highest bid, not his own bid (though the bidder with the highest bid is still the winner). Second price auctions encourage higher bidding since the winning bidder pays a lower price than his own bid.
- Dutch: In the Dutch auction, the price starts high and the auctioneer announces successively lower prices. As soon as one bidder accepts the current price, that bidder wins and pays the price, and the auction ends.
In addition to deciding the auction type, the auction designer (who may be the buyer, seller, or a third party like eBay) must decide aspects of the auction structure like how bidders may bid on multiple units (e.g., as a package or individually), what information is available to the bidders (e.g., the bids that have been placed by other bidders), and so on.
Auctions can be seen as mechanisms for supply chain coordination since they give buyers and sellers an opportunity to negotiate a mutually beneficial agreement. Game‐theoretic issues appear in auction analysis, too; for example, players may have an incentive to misrepresent their objectives through misleading bids.
In fact, there are several important properties that are desirable for auctions to have. These desirable properties include:
- Strategy‐proof: In a strategy‐proof auction, truthful bidding is never worse than untruthful bidding, for each buyer and seller. A related, but weaker, concept is incentive‐compatibility, which means that truthful bidding is a (Bayesian) Nash equilibrium.
- Ex post individually rational: An auction is ex post individually rational if each buyer and each seller do at least as well if they participate in the auction (under any auction outcome) than if they don't participate.
- Ex post budget‐balanced: An auction is ex post budget‐balanced if the auctioneer's payoff is nonnegative for all possible outcomes; therefore, the auctioneer can hold the auction without an outside subsidy.
- Optimal or efficient: An optimal auction implements an allocation that maximizes expected revenue (the sum of the expected payments of the buyers), while an efficient auction maximizes social welfare (i.e., achieves the highest possible set of awarded valuations).
Any mechanism must be individually rational and budget balanced to make an auction practical. Moreover, strategy‐proofness is desired, since each agent may not know enough information about the other agents to determine his or her optimal strategy. Unfortunately, it is not possible to design an auction mechanism that is efficient, individually rational, incentive compatible, and budget balanced—at least one of these must be sacrificed (Myerson and Satterthwaite, 1983).
In Section 15.2, we will analyze a simple English auction and show that the auction itself can be thought of in terms of a linear program and its dual. Then, in Section 15.3 we will discuss a more complicated auction with multiple products and investigate the allocation problem faced by the auctioneer. Finally, in Section 15.4, we analyze the famous Vickrey–Clarke–Groves (VCG) auction.
15.2 The English Auction
In an English auction, there is a set of bidders (also called agents), each bidding on a single item. The price begins low and gradually increases. At each price announced by the auctioneer, all bidders announce whether they are still willing to bid on the item at the current price (for example, by raising their hands), and the auction ends when only a single bidder remains. In this section, we analyze such an auction. Our analysis is adapted from Kalagnanam and Parkes (2004).
Let N be the set of agents. Agent ![]() has a valuation
has a valuation ![]() that she has assigned to the item:
that she has assigned to the item: ![]() is the maximum she'd be willing to pay for it. Paying
is the maximum she'd be willing to pay for it. Paying ![]() is like breaking even, so she'd prefer to pay less. The auctioneer knows
is like breaking even, so she'd prefer to pay less. The auctioneer knows ![]() for each bidder. His goal is to award the item to the bidder with the highest valuation. (This also maximizes the auctioneer's revenue, assuming he is the seller. However, under this auction, the auctioneer will not necessarily receive
for each bidder. His goal is to award the item to the bidder with the highest valuation. (This also maximizes the auctioneer's revenue, assuming he is the seller. However, under this auction, the auctioneer will not necessarily receive ![]() for the winning bidder.)
for the winning bidder.)
In other words, the auctioneer needs to solve the following problem:
where ![]() if agent i is awarded the item. The constraint says that at most one agent may be assigned the item. The English auction is one way of solving this problem. Another way is simply to ask each bidder for his or her valuation and to award the item to the bidder with the highest valuation, but bidders may prefer the English auction since it allows them to win the item without paying their maximum valuation.
if agent i is awarded the item. The constraint says that at most one agent may be assigned the item. The English auction is one way of solving this problem. Another way is simply to ask each bidder for his or her valuation and to award the item to the bidder with the highest valuation, but bidders may prefer the English auction since it allows them to win the item without paying their maximum valuation.
The following problem is also equivalent to (IP):
In this formulation, a new variable y is added that represents the auctioneer not assigning the item to any bidder. Then the constraint can be written as an equality instead of an inequality. Furthermore, in this formulation the integrality restriction has been dropped. We can do this because although problem (IP) is an integer program, it always has an optimal solution in which the ![]() are integer. Therefore, it is equivalent to its LP relaxation.
are integer. Therefore, it is equivalent to its LP relaxation.
Now consider the LP dual of (IP), with p the dual variable for constraint 15.5 and ![]() the dual variable for constraint 15.6:
the dual variable for constraint 15.6:
Note that p is nonnegative (constraint 15.10) since the coefficient of y in 15.4 is 0, while the nonnegativity of ![]() (constraints 15.11) follows from the inequality constraints 15.6.
(constraints 15.11) follows from the inequality constraints 15.6.
Suppose p is fixed. The optimal values of ![]() are given by
are given by ![]() . A primal solution x and a dual solution
. A primal solution x and a dual solution ![]() are optimal for their respective problems if the complementary slackness conditions hold:
are optimal for their respective problems if the complementary slackness conditions hold:
The dual variables p and ![]() have a natural interpretation in the context of the auction: p is the selling price of the item and
have a natural interpretation in the context of the auction: p is the selling price of the item and ![]() is the payoff (valuation minus price) to agent i under price p. The complementary slackness conditions are then interpreted as follows:
is the payoff (valuation minus price) to agent i under price p. The complementary slackness conditions are then interpreted as follows:
- If the price is positive, then by CS1 either someone gets it or no one gets it. By CS4, if no one gets it, then the price must be 0. So taken together, CS1 and CS4 mean if the price is positive, someone gets the item.
- By CS3, if agent i wins the auction, then the price must equal
 ; since
; since  by 15.11, this means the winning agent pays no more than his valuation.
by 15.11, this means the winning agent pays no more than his valuation. - By CS2, any agent not receiving the item (
 ) must have
) must have  ; this means
; this means  by 15.9, i.e., the price is greater than the losing agent's valuation.
by 15.9, i.e., the price is greater than the losing agent's valuation.
Notice that these are exactly the conditions under which the auction ends.
The simplex method is called a primal algorithm for solving LPs because it maintains a primal solution at all times and tries to improve it until it finds the optimal solution. Other methods, called primal–dual algorithms, maintain both a primal and a dual solution at all times and attempt to move toward optimal solutions by fixing violations in the complementary slackness conditions.
This is exactly the process taken by the English auction! In a sense, the auction is nothing more than a big LP solver in which the actions of the players correspond to steps in the algorithm. In particular, interpret the dual variable p as the current price and the dual variables ![]() as the corresponding payoffs for each agent. Interpret the primal variable
as the corresponding payoffs for each agent. Interpret the primal variable ![]() as indicating whether agent i is the current “provisional” winner of the auction, chosen arbitrarily from among the bidders that are still interested in the item at the current price p. Interpret y as indicating that no bidders are still interested in the item at the current price. Throughout the auction, the primal and dual solutions are both feasible for their respective problems. When the complementary slackness conditions hold, the auction ends, the optimal solutions having been found. Note that in every round, CS1, CS3, and CS4 hold in the auction: If the price is positive, some agent must be the current provisional winner (CS1 and CS4), and the price is less than the value of the provisional winner (CS3). CS2 might not hold since there may be nonwinners who still have a positive payoff, that is, whose valuations are less than the current price. The primal‐dual approach works by increasing p until CS2 holds.
as indicating whether agent i is the current “provisional” winner of the auction, chosen arbitrarily from among the bidders that are still interested in the item at the current price p. Interpret y as indicating that no bidders are still interested in the item at the current price. Throughout the auction, the primal and dual solutions are both feasible for their respective problems. When the complementary slackness conditions hold, the auction ends, the optimal solutions having been found. Note that in every round, CS1, CS3, and CS4 hold in the auction: If the price is positive, some agent must be the current provisional winner (CS1 and CS4), and the price is less than the value of the provisional winner (CS3). CS2 might not hold since there may be nonwinners who still have a positive payoff, that is, whose valuations are less than the current price. The primal‐dual approach works by increasing p until CS2 holds.
15.3 Combinatorial Auctions
Englishauctions involve only a single item for sale. In this section, we will discuss auctions in which there are a number of heterogeneous items for sale. In such an auction, bidders may want to bid on combinations of items instead of individual items. For example, suppose you attend an auction of some antique furniture. You might be interested in buying the bed and matching dresser if you could buy them together, but might not be interested in buying only one of them. Or, you might be interested in buying one bed or another, but not both. Valuation, then, is assigned to subsets of items (called bundles) rather than to individual items. This makes the auction itself, as well as the auctioneer's allocation problem, considerably more complex. Such auctions are called combinatorial auctions. Our analysis of combinatorial auctions is adapted from de Vries and Vohra (2003). For further discussion of combinatorial auctions in practice, see Harstad and Pekeč (2008).
A famous example of a combinatorial auction is the occasional auction of telecommunications spectrum rights held by the US Federal Communications Commission (FCC). A cell phone carrier, for example, might want to buy one license in each market it's interested in. Bidding for individual licenses misses the point since the value of one license depends on which other licenses the company holds. In the FCC's first auction, in 1994, they allowed bids on individual licenses only (though steps were taken to help bidders obtain bundles they were interested in), thinking it would be too cumbersome to allow bids on bundles. However, in 2003, the FCC held its first auction in which bidders could bid on combinations of licenses.
Another example of a practitioner of combinatorial auctions is JUNAEB, the agency responsible for providing free meals to low‐income schoolchildren in Chile. Since 1980, the agency has used auctions to select private companies to provide these meals throughout the country. Companies place bids that indicate the geographic region they will serve, the services they will provide, and the price they will charge. Prior to 1997, bids were chosen more or less independently, without considering the interdependencies among the bids. But in 1997, JUNAEB began using combinatorial auctions to allocate bids. Each company can submit multiple bids, for example, covering different combinations of geographical regions. The new auction mechanism saves JUNAEB an estimated US$40 million per year and has also improved the quality of the food, the geographic scope of the assistance program, and the transparency of the entire bidding process (Epstein et al., 2004).
15.3.1 The Combinatorial Auction Problem
Let M be the set of objects being auctioned off, and let N be the set of bidders. For any bundle ![]() , let
, let ![]() be the bid that agent i has announced he is willing to pay for S. Note that b is different from v since it represents announced bids, not valuations; an agent's bid for a bundle might be less than his valuation. In an auction of any reasonable size, it would be impossible for an agent to specify a bid for all
be the bid that agent i has announced he is willing to pay for S. Note that b is different from v since it represents announced bids, not valuations; an agent's bid for a bundle might be less than his valuation. In an auction of any reasonable size, it would be impossible for an agent to specify a bid for all ![]() possible bundles, so you can think of b as a function that takes a bundle suggested by the auctioneer and returns a bid for that bundle. Without loss of generality we can assume
possible bundles, so you can think of b as a function that takes a bundle suggested by the auctioneer and returns a bid for that bundle. Without loss of generality we can assume ![]() for all
for all ![]() . Let
. Let ![]() be 1 if agent i is assigned bundle
be 1 if agent i is assigned bundle ![]() and 0 otherwise.
and 0 otherwise.
The auctioneer's problem is to allocate the bundles to agents in order to maximize her revenue. This problem is known as the combinatorial auction problem (CAP) and is formulated as follows:
The objective function maximizes the revenue to the seller. (If the bids are equal to the actual valuations, then this formulation also maximizes the “efficiency” of the auction—assigning bundles to the agents that value them the highest.) Constraints 15.13 ensure that no two bundles assigned to agents contain the same item. (The summation over ![]() is a summation over all
is a summation over all ![]() that contain j.) Constraints 15.14 prevent an agent from receiving more than one bundle. This is necessary to ensure that the auctioneer does not decide to assign bundles S and T to bidder i, instead of
that contain j.) Constraints 15.14 prevent an agent from receiving more than one bundle. This is necessary to ensure that the auctioneer does not decide to assign bundles S and T to bidder i, instead of ![]() , if
, if ![]() . However, we will restrict ourselves to cases in which a bid for a bundle is no smaller than the sum of bids of subsets of the bundle; that is,
. However, we will restrict ourselves to cases in which a bid for a bundle is no smaller than the sum of bids of subsets of the bundle; that is, ![]() for all
for all ![]() . Bid functions for which this property holds are called superadditive. If the bid functions are superadditive, then constraints 15.14 are no longer needed since it is always to the seller's advantage to award an agent a single bundle rather than two separate ones.
. Bid functions for which this property holds are called superadditive. If the bid functions are superadditive, then constraints 15.14 are no longer needed since it is always to the seller's advantage to award an agent a single bundle rather than two separate ones.
We now reformulate (CAP) as an instance of the set packing problem (SPP), in which there is a set M of elements and a collection V of subsets of M with nonnegative weights; the objective is to choose the largest‐weight collection of subsets such that every element is contained in at most one subset. (The SPP is like the inverse of the set covering problem (Section 8.4.1), in which we want to choose subsets such that every element is contained in at least one subset. If every element must be contained in exactly one subset, we have the set‐partitioning problem.)
Let V be the collection of all subsets of M, and let k be an individual bundle (subset). Define
that is, ![]() is the maximum bid any agent would be willing to pay for bundle k. Let
is the maximum bid any agent would be willing to pay for bundle k. Let ![]() if bundle k contains item i, 0 otherwise. Finally, let
if bundle k contains item i, 0 otherwise. Finally, let ![]() if bundle k is selected, 0 otherwise. The problem now reduces to one of partitioning the items into bundles; the actual assignments can be done after the fact based on which agent maximized
if bundle k is selected, 0 otherwise. The problem now reduces to one of partitioning the items into bundles; the actual assignments can be done after the fact based on which agent maximized ![]() for each selected bundle k. The CAP can be reformulated as:
for each selected bundle k. The CAP can be reformulated as:
Constraints 15.17, like constraints 15.13, prohibit the bundles from overlapping. We will focus on this formulation of the CAP in what follows.
15.3.2 Solving the Set‐Packing Problem
Unlike the auctioneer's problem in the English auction, the CAP does not naturally have all integer solutions; that is, it is not equivalent to its LP relaxation. Therefore, we can't use LP duality to solve the problem. However, we will use Lagrangian relaxation (which provides a different type of duality) to solve it and show that, like the LP dual, the Lagrangian formulation has a natural interpretation in the auction context.
Let's relax constraints 15.17 in the SPP using Lagrange multipliers ![]() . The resulting subproblem is
. The resulting subproblem is

Solving (SPP‐LRλ) is easy: For each ![]() we set
we set ![]() if
if
and 0 otherwise. Since (SPP) is a maximization problem, for a given ![]() ,
, ![]() provides an upper bound on that of (SPP), and our goal is to find better (i.e., smaller) upper bounds by solving
provides an upper bound on that of (SPP), and our goal is to find better (i.e., smaller) upper bounds by solving
Note that ![]() is restricted to be nonnegative; see Section D.1.5. Problem (SPP‐LR) is sometimes known as the Lagrangian dual, because in many ways it behaves like an LP dual. (SPP‐LR) can be solved approximately using subgradient optimization, as we did when using Lagrangian relaxation in Chapter 8. A solution to (SPP‐LRλ) can be converted into a feasible solution for (SPP) using some heuristic; this feasible solution then provides a lower bound.
is restricted to be nonnegative; see Section D.1.5. Problem (SPP‐LR) is sometimes known as the Lagrangian dual, because in many ways it behaves like an LP dual. (SPP‐LR) can be solved approximately using subgradient optimization, as we did when using Lagrangian relaxation in Chapter 8. A solution to (SPP‐LRλ) can be converted into a feasible solution for (SPP) using some heuristic; this feasible solution then provides a lower bound.
Our interest is not so much in this solution method as in its auction interpretation. The Lagrange multiplier![]() represents the price on an individual item set by the auctioneer. The agents have already announced their bids for each bundle
represents the price on an individual item set by the auctioneer. The agents have already announced their bids for each bundle ![]() , the maximum of which is
, the maximum of which is ![]() . If
. If ![]() , then, according to the solution to ( SPP‐LRλ),
, then, according to the solution to ( SPP‐LRλ), ![]() is set to 1—the bundle is temporarily included in the group of bundles to be sold. Presumably, the bundles in that group may overlap (constraints 15.17 may be violated), in which case the auctioneer must adjust the prices
is set to 1—the bundle is temporarily included in the group of bundles to be sold. Presumably, the bundles in that group may overlap (constraints 15.17 may be violated), in which case the auctioneer must adjust the prices ![]() using subgradient optimization. Prices for items that are included in too many bundles would increase, while prices for items that are in no bundles would decrease.
using subgradient optimization. Prices for items that are included in too many bundles would increase, while prices for items that are in no bundles would decrease.
As in the English auction, feasible solutions to the dual problem represent prices, while feasible solutions to the primal problem represent tentative assignments of items to agents. A primal‐dual pair is optimal if something akin to the complementary slackness conditions hold:
- If
 , then
, then  , i.e., item j is contained in exactly one allocated bundle. Another way of saying this is that if j is not included in any bundle, then it is a worthless item, so
, i.e., item j is contained in exactly one allocated bundle. Another way of saying this is that if j is not included in any bundle, then it is a worthless item, so  .
. - If
 , then
, then  , i.e., the bundle is worth at least the asking price tosome bidder.
, i.e., the bundle is worth at least the asking price tosome bidder.
15.3.3 Truthful Bidding
In the combinatorial auction described above, the seller allocates bundles to maximize her revenue based on the bids. But there is no guarantee that the bids accurately reflect the bidders' valuations of the items, and bidders may have an incentive to lie. For example, suppose there are three bidders (1, 2, and 3) and two items (A and B). The bidders' valuations of the three possible bundles are given in Table 15.1.
Table 15.1 Valuations that induce nontruthful bidding.
| Bundle | |||
| Bidder | A | B | A,B |
| 1 | 0 | 0 | 100 |
| 2 | 75 | 75 | 0 |
| 3 | 40 | 40 | 0 |
The bidders do not need to place bids equal to their valuations. If they did bid truthfully, the auctioneer should award A to 2 and B to 3 (or vice‐versa), for a revenue of 115. However, if bidder 2 assumes that bidder 3 will continue to bid truthfully, he has an incentive to reduce his bid on A and B, say, to 65. Bidders 2 and 3 still win the auction, but bidder 2 pays less. Bidder 3 can reason the same way—but if they both reduce their bids, bidder 1 might win the auction.
If bidders 2 and 3 could collude on their bids, they could ensure that they win the auction, as long as the sum of their bids (for each item) is greater than 100, though this leaves a profit of 15 that they need to decide how to share.
Obviously, it is to the auctioneer's advantage if the agents bid truthfully. She can't force them to do so, but she can design the auction mechanism so that the bidders' optimal strategy is to bid truthfully. This is very similar to the supply chain contracts discussed in Chapter 14: By structuring the payoffs carefully, the mechanism designer motivates the players to behave in a particular way, even when they are acting selfishly. In the case of auctions, however, the auctioneer is trying to manipulate the game so that the agents maximize her own revenue, while in supply chain contracting, the contracts are designed to maximize the common revenue.
15.4 The Vickrey–Clarke–GrovesAuction
15.4.1 Introduction
In this section, we discuss an auction mechanism in which it is to the agents' benefit to bid truthfully. The auction is called the Vickrey–Clarke–Groves (VCG) auction, after the researchers who proposed and studied it. The VCG auction is a single‐round sealed‐bid auction. (If there is only a single item, it is equivalent to a sealed‐bid second‐price auction.) It works as follows:
- Agent i reports his valuation
 for all
for all  . There is nothing to prevent the agents from misreporting their valuations, but it turns out to be optimal for them to be truthful.
. There is nothing to prevent the agents from misreporting their valuations, but it turns out to be optimal for them to be truthful. - The auctioneer solves the following problem:

Note that this is just (CAP) with b replaced by v. Let
 be the optimal solution.
be the optimal solution. - The auctioneer solves the following problem for each agent
 :
: 
This is the allocation problem assuming that player k does not participate in the auction.
- Bundles are awarded to agents according to
 . The payment that agent k pays is equal to
. The payment that agent k pays is equal to
Note that the VCG auction awards bundles in the same manner as the combinatorial auction in Section 15.3.1, but the payments are different.
Here is the logic behind 15.21. ![]() is the “welfare” of the other agents when agent k is excluded from the auction. The term inside the brackets is the welfare of the other agents when agent k participates. So agent k's payment is equal to the difference in the other agents' welfare without him and with him. In other words, agent k reimburses the system for the value that he has taken away by winning his bundle.
is the “welfare” of the other agents when agent k is excluded from the auction. The term inside the brackets is the welfare of the other agents when agent k participates. So agent k's payment is equal to the difference in the other agents' welfare without him and with him. In other words, agent k reimburses the system for the value that he has taken away by winning his bundle.
Why does agent k have an incentive to tell the truth when he reports ![]() ? First notice that changing
? First notice that changing ![]() doesn't affect
doesn't affect ![]() since the
since the ![]() auction excludes agent k. Moreover, the term inside the brackets in 15.21 is equal to the optimal objective value of the allocation problem minus agent k's payment. So that term is independent of
auction excludes agent k. Moreover, the term inside the brackets in 15.21 is equal to the optimal objective value of the allocation problem minus agent k's payment. So that term is independent of ![]() . Therefore, a winning agent's payment will not change if he under‐ or over‐states his valuation. Finally, if an agent over‐states his valuations in the hope of winning a bundle that he wouldn't have won under truthful bidding, then he will pay more for this bundle than his valuation—see Problem 15.4. Therefore, agents have no incentive to misrepresent their valuations when they bid.
. Therefore, a winning agent's payment will not change if he under‐ or over‐states his valuation. Finally, if an agent over‐states his valuations in the hope of winning a bundle that he wouldn't have won under truthful bidding, then he will pay more for this bundle than his valuation—see Problem 15.4. Therefore, agents have no incentive to misrepresent their valuations when they bid.
If the seller implements the VCG auction, her total revenue will be
If the number of bidders is large, then V will tend to be very close to ![]() since no single agent would have too large an effect on the auction. Therefore, the seller's revenue is close to V, which is the maximum revenue any auction could earn.
since no single agent would have too large an effect on the auction. Therefore, the seller's revenue is close to V, which is the maximum revenue any auction could earn.
It is well known that the VCG mechanism is strategy proof, ex post individually rational, and efficient. However, the VCG mechanism is not budget balanced; that is, it is possible that the auctioneer may receive a negative payoff. In a one‐sided auction such as the one discussed here (with a single seller and multiple buyers), the budget imbalance arises from the fact that the auctioneer's valuations for the items are not considered in the allocation problem or payment calculation, and therefore the auctioneer could receive payments that fall short of her valuation for the items sold. (In Example 15.1, if the auctioneer's total valuation for the two books is 200, then she receives a negative payoff.) The same is true for VCG mechanisms in more complicated settings, such as double auctions (with multiple buyers and sellers).
Recently, there has been a focus on using auctions for supply chain procurement and trading in e‐marketplaces. The benefits of auctions include lower information, transaction, and participation costs; increased convenience for both sellers and buyers; and, consequently, better market efficiency. While research and practice in operations management have emphasized optimizing the total supply chain, classical auction theory does not consider the operational costs associated with integrating a supply chain, such as logistics and inventory management costs. More recent work attempts to include these costs into the auction design. For example, Chen et al. (2005) consider combinatorial procurement auctions in supply chain settings. They incorporate supply chain costs (e.g., transportation costs in a complex supply chain network) into VCG auctions. Chu and Shen (2006,2008) propose several double‐auction mechanisms for e‐marketplaces. Under their proposed double‐auction mechanisms, bidding one's true valuation is the optimal strategy for each individual buyer and seller, even when shipping costs and sales taxes are different across various possible transactions. The proposed mechanism also achieves budget balance and asymptotic efficiency (that is, the auction approaches the maximum social welfare as the number of buyers and/or sellers approaches infinity). Furthermore, these results not only hold for an environment in which buyers and sellers exchange identical commodities, but also can be extended to more general environments, such as multiple substitutable commodities and bundles of commodities.
15.4.2 Weaknesses of the VCG Auction
Despite its impressive theoretical virtues of being strategy‐proof, ex post individually rational and efficient, the VCG auction also suffers from several weaknesses that limit its usefulness in practice. In this section, we demonstrate some of these weaknesses using examples adapted from Ausubel and Milgrom (2006).
The first weakness of the VCG auction is that the auctioneer's revenues can be very low or zero, even when the items are valuable and the there are many competing bidders. We already know from Section 15.4.1 that the auctioneer's payoff—her revenue minus valuation—could be negative. Here we are arguing that her revenue could even be very small. The next example illustrates this.
Since the final auction revenue is one of the most important attributes for the auctioneer, the fact that the VCG auction can result in such small revenues for the auctioneer is a huge strike against it in practice.
Not only can the auctioneer's revenue be small, it is not, in general, monotonic in either the number of bidders or their valuations. We would expect that when the number of bidders increases, or their bids increase, the auctioneer's revenue should also increase, but this is not necessarily the case, as the next example demonstrates. Therefore, in the VCG auction, the auctioneer may prefer to prevent new bidders, or high‐valuation bidders, from entering the auction, which is counterintuitive.
Third, although we know from Section 15.4.1 that truthful bidding is a dominant strategy for each individual bidder in the VCG auction, it turns out that losing bidders can sometimes profit by colluding to deviate from their true valuations. In general, it is undesirable for an auction mechanism to incentivize collusion—another strike against VCG.
A fourth weakness of the VCG auction is that it is vulnerable to bidders establishing multiple identities, i.e., a single bidder representing herself as multiple bidders. The next example demonstrates.
In summary, in addition to the computational complexity of solving the CAP, the examples above reveal important defects of the VCG auction—revenue deficiency, nonmonotonicity of the auctioneer's revenue, and a vulnerability to both collusion and multiple identities—that make it unappealing for most practical applications. For further discussion of these and other defects, see Ausubel and Milgrom (2006).
An important question is, under what conditions can these defects be eliminated? We will characterize one such condition from the perspective of game theory in the next section.
15.4.3 VCG Auction as a Cooperative Game
Theexamples in Section 15.4.2 demonstrate that the auctioneer's revenue in the VCG auction can be very low, even when the bidders' valuations for the items are high. A natural question is, how much revenue is acceptable for the auctioneer if we regard both the auctioneer and the bidders as players in a cooperative game? To answer this question, we will analyze the core of the game, which contains the payoff vectors from which no subset of the players—called a coalition—has an incentive to deviate. The core thus generalizes the concept of Nash equilibrium in a noncooperative game, which is a payoff vector from which no single agent has an incentive to deviate. Therefore, if the payoff vector (or allocation) of the VCG auction lies in the core, we consider the corresponding auctioneer's revenue to be acceptable.
In what follows, we first formulate the VCG auction as a cooperative game and show that the payoff vector is beneficial for the bidders. Next, we introduce a submodularity condition that guarantees that the VCG payoff vector lies in the core, and thus the whole coalition won't break. Finally, we briefly discuss a condition on the bidders' preferences that ensures that the submodularity condition holds, and therefore that the weaknesses discussed in Section 15.4.2 will never occur.
As usual, let N be the set of bidders and let M be the set of objects being auctioned off. Let 0 represent the auctioneer, and denote the set of all players as ![]() . The coalitional value function is defined for coalitions
. The coalitional value function is defined for coalitions ![]() as the maximum total value the coalition can create by trading among themselves, if the coalition includes the auctioneer; otherwise, the function equals zero. Here, we implicitly assume that the valuation of the auctioneer for any bundle is zero. Mathematically, for any
as the maximum total value the coalition can create by trading among themselves, if the coalition includes the auctioneer; otherwise, the function equals zero. Here, we implicitly assume that the valuation of the auctioneer for any bundle is zero. Mathematically, for any ![]() such that
such that ![]() , the coalitional value function is
, the coalitional value function is

where, as usual, ![]() is the valuation of bidder i for bundle S. In other words,
is the valuation of bidder i for bundle S. In other words, ![]() is the optimal objective function value of the auctioneer's problem in the VCG auction, with N replaced by
is the optimal objective function value of the auctioneer's problem in the VCG auction, with N replaced by ![]() .
.
The core of a game with player set L and coalitional value function ![]() is defined as follows:
is defined as follows:

The core contains all payoff vectors ![]() so that the coalitional value function of the whole player set equals the sum of the payoffs, and so that no smaller coalition could do any better than
so that the coalitional value function of the whole player set equals the sum of the payoffs, and so that no smaller coalition could do any better than ![]() if they excluded the other players. In other words, any payoff vector in the core is feasible, and the corresponding outcome is stable, in the sense that there is no coalition with the desire to change the outcome of the game. Thus, any payoff vector in the core is also referred to as a competitive outcome, for which it is impossible for the auctioneer and a subset of bidders to block the auction by defecting and negotiating an outcome with higher payoffs for themselves. Classical economic theory typically treats the core as the solution to a game‐theoretic problem. From the perspective of game theory, a given type of auction is no more than a way to determine the payoff allocations in a game consisting of the auctioneer and bidders. In what follows, we discuss under what conditions the payoff vector of the VCG auction lies in the core. Our analysis is adapted from Ausubel and Milgrom (2006).
if they excluded the other players. In other words, any payoff vector in the core is feasible, and the corresponding outcome is stable, in the sense that there is no coalition with the desire to change the outcome of the game. Thus, any payoff vector in the core is also referred to as a competitive outcome, for which it is impossible for the auctioneer and a subset of bidders to block the auction by defecting and negotiating an outcome with higher payoffs for themselves. Classical economic theory typically treats the core as the solution to a game‐theoretic problem. From the perspective of game theory, a given type of auction is no more than a way to determine the payoff allocations in a game consisting of the auctioneer and bidders. In what follows, we discuss under what conditions the payoff vector of the VCG auction lies in the core. Our analysis is adapted from Ausubel and Milgrom (2006).
Let ![]() be the VCG payoff vector. Specifically,
be the VCG payoff vector. Specifically, ![]() is the payoff of bidder
is the payoff of bidder ![]() :
:
(Recall that the payoff is the valuation minus the price. The first term in 15.23 is the bidder's valuation, and the second is the price, from 15.21.) Similarly, ![]() is the payoff of the auctioneer, 0:
is the payoff of the auctioneer, 0:
(See 15.22.)
The following Lemma shows that the core ![]() is nonempty, and that every bidder's payoff in the VCG auction is the greatest among all points in the core of
is nonempty, and that every bidder's payoff in the VCG auction is the greatest among all points in the core of ![]() .
.
We say that a payoff vector ![]() is bidder dominant if it lies in the core and if, for any
is bidder dominant if it lies in the core and if, for any ![]() , we have
, we have ![]() for every bidder
for every bidder ![]() . In other words,
. In other words, ![]() is bidder dominant if it is in the core and if it is at least as good as every other vector in the core, for every bidder. From Lemma 15.1, we have the following result.
is bidder dominant if it is in the core and if it is at least as good as every other vector in the core, for every bidder. From Lemma 15.1, we have the following result.
Theorem 15.1 shows that the auctioneer's revenue from the VCG auction is strictly smaller than his revenue in any competitive outcome, unless the VCG payoff vector lies in the core.
Next we give conditions on the coalitional value function that ensure that the VCG payoff vector lies in the core, regardless of which potential bidders decide to participate in the auction. To that end, define ![]() as a payoff vector in the game in which the players are exactly the members of coalition S:
as a payoff vector in the game in which the players are exactly the members of coalition S:

We say that the coalitional value function ![]() is bidder‐submodular if, for all
is bidder‐submodular if, for all ![]() and all coalitions S and
and all coalitions S and ![]() such that
such that ![]() ,
,
The following theorem shows that bidder‐submodularity is a necessary and sufficient condition such that the VCG payoff vector lies in the core, and thus the auctioneer's VCG payoff meets the competitive benchmark.
Theorem 15.2 shows under what conditions on the coalitional value function the (restricted) VCG payoff vector lies in the core. Unfortunately, it is difficult for the auctioneer to know the coalition value function in advance. Therefore, it is worth investigating conditions under which the individual preferences guarantee that the VCG payoff vector lies in the core. See Ausubel and Milgrom (2006) for a further discussion ofthis issue.
PROBLEMS
- 15.1 (Nonoptimality of the English Auction) Suppose you have decided to sell a valuable collection of baseball paraphernalia. You have identified N potential buyers for the collection. In this problem, you will consider two alternate ways of selling the collection, one involving an auction and one not. You are selling the collection as a whole, not as individual parts.
Each of the N bidders has a valuation
 for the collection. You do not know the
for the collection. You do not know the  s for each bidder, but you do know that each bidder's valuation is independently and uniformly distributed on
s for each bidder, but you do know that each bidder's valuation is independently and uniformly distributed on  .
.Your first idea involves simply setting a price p and offering the collection for sale at that price. If some bidder wants to buy the item at that price (i.e., if
 for some bidder), he or she buys the item. If there are multiple such bidders, one is chosen randomly. If there are no such bidders, the sale ends unsuccessfully.
for some bidder), he or she buys the item. If there are multiple such bidders, one is chosen randomly. If there are no such bidders, the sale ends unsuccessfully.- Let
 be the probability that you sell the collection if you set the price to p. Calculate
be the probability that you sell the collection if you set the price to p. Calculate  . (Your answer should be in terms of N.)
. (Your answer should be in terms of N.) - Write your expected revenue as a function of p.
- Calculate the optimal price
 , the probability of selling the collection at this price, and the corresponding expected revenue.
, the probability of selling the collection at this price, and the corresponding expected revenue. - Show that the optimal revenue is strictly increasing in N.
Next you consider selling the collection using an English auction, in which you start the price at $0 and gradually increase it until only one bidder remains. Assume that you increase the price continuously (infinitesimally), and that a bidder will not bid if the price equals his or her valuation (only if it's strictly less).
- Argue that the English auction always results in the winning bidder paying the second‐highest valuation.
- The expected value of the second largest of N random variables that are iid
 is equal to
is equal to  . Use this fact to show that the expected revenue from the English auction is smaller than that from the nonauction method if
. Use this fact to show that the expected revenue from the English auction is smaller than that from the nonauction method if  or 2 and is larger if
or 2 and is larger if 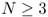 . Therefore, the English auction is not optimal from the seller's perspective if
. Therefore, the English auction is not optimal from the seller's perspective if  .
. - Prove that, in the optimal solution to problem (D) on page 8 for this auction, p is equal to the second‐highest valuation
 .
. - Verify the result from part (g) by solving problem (LP) for the data in Table 15.9 using an LP solver of your choice. That is, verify that
 for the bidder with the highest valuation but that p, the dual value for constraint 15.5, equals the second‐highest valuation.
for the bidder with the highest valuation but that p, the dual value for constraint 15.5, equals the second‐highest valuation. Table 15.9 Valuations for English auction in Problem 15.1. Bidder (i) Valuation (  )
)1 100 2 120 3 135 4 85 5 90
- Let
- 15.2 (LP Relaxation of (CAP)) Construct a small example (using as few bidders and items as possible) for which the LP relaxation of (CAP) does not have an integer optimal solution.
- 15.3 (VCG Auction for Candy Shipments) The Truck o' Treats Company, a shipping company that specializes in refrigerated shipments of candy, will send a truck next week from Bethlehem, PA, to Chicago, IL, and from there to Berkeley, CA. The current load is insufficient to fill the truck, and the company plans to use a VCG auction to sell the remaining 1000 cubic feet of capacity to a candy company that needs to ship goods along those routes. (The remaining capacity is the same on both legs of the route because the truck will make a delivery in Chicago but pick up an equal volume of goods for shipment to Berkeley.)
Four candy companies each have 1000 cubic feet of candy to ship and are considering bidding for the routes. Horseshoe Candy needs to ship candy from Bethlehem to Chicago and is willing to pay up to $900 for this leg; however, they have no product to ship to Berkeley and do not wish to bid for the second leg. Ares Chocolates, in contrast, has product to ship from Chicago to Berkeley (for which it is willing to pay $1150) but nothing to ship from Bethlehem to Chicago. Valhalla Chocolates has goods to ship to both destinations; it is willing to pay $600 to ship from Bethlehem to Chicago and $1200 to ship from Chicago to Berkeley; however, if they can do both, they are willing to pay $2000 to avoid the hassle of using two separate shipments. Similarly, W&W Candies is willing to pay $800 for the Bethlehem–Chicago leg, $950 for Chicago–Berkeley, and $1900 for both.
What leg(s) will be awarded to each company in the outcome of the VCG auction, and what will each winning bidder pay? What will be the total revenue to Truck o' Treats? Construct a table like Table 15.3 that lists the bids, values of awarded items,
 values, and payments.
values, and payments. - 15.4 (Misrepresenting Valuations in the VCG Auction) Prove that, in the VCG auction, a bidder does not have an incentive to bid greater than his valuation (in an attempt to win a bundle that he otherwise would not have won). In particular, suppose that bidder k is not awarded a particular bundle
 if all bidders state their true valuations. Prove that if bidder k over‐states his valuation for bundle T to such an extent that he is now awarded bundle T, then the price he pays for bundle T will be greater than or equal to
if all bidders state their true valuations. Prove that if bidder k over‐states his valuation for bundle T to such an extent that he is now awarded bundle T, then the price he pays for bundle T will be greater than or equal to  , his true valuation for bundle T.
, his true valuation for bundle T. To keep things simple, you may assume that bidder k does not receive any bundle when all bidders state their true valuations, and that when bidder k over‐states his valuation for T, the rest of the bundles are awarded to the same bidders that they were awarded to originally; that is, the allocation of bundle T may change, but no other bundles. Furthermore, assume the partitioning of items into bundles does not change.
Hint: First prove the result for a single‐item, second‐price auction.
- 15.5 (Double Auctions) Adouble auction consists of multiple buyers and multiple sellers. Potential buyers submit their bids and potential sellers simultaneously submit their ask prices to an auctioneer. The auctioneer first eliminates some sellers who ask too much and some buyers who offer too little, and then decides which of the remaining buyers and sellers will transact with each other, and at what price. Transactions incur costs, which may represent costs associated with transportation, quality, lead time, customization, and the buyer–vendor relationship. The transaction costs are assumed to be common knowledge.
Suppose there are multiple commodities to be exchanged in the auction. There is a collection of sellers, each of whom offers for sale a single unit of a single commodity, facing a collection of buyers, each interested in buying a bundle consisting of multiple commodities, but at most one of each. Formulate the problem of maximizing social welfare assuming all agents bid truthfully. Use the following notation:
I set of buyers J set of sellers C set of indivisible commodities 
bid price of buyer i for her bundle 
ask price of seller j for his item 
 , a bundle of goods that buyer i (
, a bundle of goods that buyer i ( ) wants to procure;
) wants to procure; if buyer i wants to procure one unit of commodity c and 0 otherwise
if buyer i wants to procure one unit of commodity c and 0 otherwise
 , supply offered by seller j (
, supply offered by seller j ( );
); if seller j supplies one unit of commodity c and 0 otherwise
if seller j supplies one unit of commodity c and 0 otherwise
transaction cost when buyer i purchases commodity c from seller j - 15.6 (Single‐Commodity Double Auctions) Consider a simpler version of the double auction in Problem 15.5 in which there is only a single commodity. Assume that when buyer i trades with seller j, transaction cost
 is incurred.
is incurred.- Formulate the single‐commodity double auction.
- Show that the simplified formulation can be solved efficiently.
- Consider an example with two sellers and three buyers. The transaction cost matrix is given in Table 15.10. The agents have an incentive to truthfully bid their valuations, which are shown in Figure 15.1. Determine which buyer(s) transact with which seller(s) in the efficient allocation. How much should the winning buyers pay? How much should the winning sellers receive?
Table 15.10 Transaction costs for double auction in Problem 15.6. 
1 2 1 4 7 2 6 4 3 9 6 
Figure 15.1 Bidders' valuations in double auction in Problem 15.6.
- 15.7 (VCG Payoff Vector and Core) Consider a combinatorial auction with three items and four bidders. The bidders' valuations of the possible bundles are given in Table 15.11.
- Suppose all bidders state their true valuations. Compute the auctioneer's revenue from the VCG auction, the bidders' payments, and the VCG payoff vector.
- Does the VCG payoff vector lie in the core? If not, identify a coalition that will block this result.
Table 15.11 Valuations for VCG auction in Problem 15.7. Bidder (i) 






1 4 2 2 4 4 3 8 2 3 5 2 3 5 5 8 3 4 2 6 4 5 3 7 4 2 2 2 3 4 4 10



