7.3 Informative stopping rules

7.3.1 An example on capture and recapture of fish

A stopping rule s is said to be informative if its distribution depends on θ in such a way that it conveys information about θ in addition to that available from the values of . The point of this section is to give a non-trivial example of an informative stopping rule; the example is due to Roberts (1967).

Consider a capture–recapture situation for a population of fish in a lake. The total number N of fish is unknown and is the parameter of interest (i.e. it is the θ of the problem). It is known that R of the fish have been captured tagged and released, and we shall write S for the number of untagged fish. Because S=N–R and R is known, we can treat S as the unknown parameter instead of N, and it is convenient to do so. A random sample of n fish is then drawn (without replacement) from the lake. The sample yields r tagged fish and S=N–R untagged ones.

Assume that there is an unknown probability of catching each fish independently of each other. Then the stopping rule is given by the binomial distribution as

so that is a nuisance parameter such that . Note that this stopping rule is informative, because it depends on N=R+S.

Conditional on R, N, and n, the probability of catching r tagged fish out of n=r+s is given by the hypergeometric distribution

Because we know r and s if and only if we know r and n, it follows that

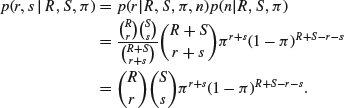
7.3.2 Choice of prior and derivation of posterior

We assume that not much is known about the number of the fish in the lake a priori, and we can represent this by an improper prior

On the other hand, in the process of capturing the first sample R for tagging, some knowledge will have been gained about the probability of catching a fish. Suppose that this knowledge can be represented by a beta prior, so that , that is,

independently of S. It follows that

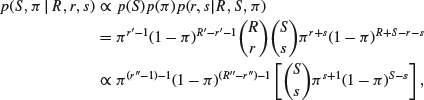
where

It follows that for given the distribution of S is such that S–s has a negative binomial distribution (see Appendix A). Summing over S from s to , it can also be seen that

so that the posterior for is .

To find the unconditional distribution of S, it is necessary to integrate the joint posterior for S and over . It can be shown without great difficulty that the result is that

where is the usual beta function. This distribution is sometimes known as the beta-Pascal distribution, and its properties are investigated by Raiffa and Schlaifer (1961, Section 7.11). It follows from there that the posterior mean of S is

from which the posterior mean of N follows as N=R+S.

7.3.3 The maximum likelihood estimator

A standard classical approach would seek to estimate S or equivalently N by the maximum likelihood estimator, that is, by the value of N which maximizes

Now it is easily shown that

and this increases as a function of S until it reaches unity when (r+s)S=(R+S)s and then decreases, so that the maximum likelihood estimator of S is

7.3.4 Numerical example

As a numerical example, suppose that the original catch was R = 41 fish and that the second sample results in r = 8 tagged and s = 24 untagged fish. Suppose further that the prior for the probability of catching a fish is , so that

(so that and ). Then the posterior mean of S is

and hence that of N is , that is, 41+199=240. On the other hand, the same data with a reference prior for (i.e. ) results in a posterior mean for S of

and hence that of N is 41+161.5=202.5.

Either of these answers is notably different from the maximum likelihood answer that a classical statistician would be likely to quote, which is

resulting in . The conclusion is that an informative stopping rule can have a considerable impact on the conclusions, and (though this is scarcely surprising) that prior beliefs about the nuisance parameter make a considerable difference.