7.2 The stopping rule principle

7.2.1 Definitions

We shall restrict ourselves to a simple situation, but it is possible to generalize the following account considerably; see Berger and Wolpert (1988, Section 4.2). Basically, in this section, we will consider a sequence of experiments which can be terminated at any stage in accordance with a rule devised by the experimenter (or forced upon him).

Suppose that the observations are independently and identically distributed with density and let

We say that s is a stopping rule or a stopping time if it is a random variable whose values are finite natural numbers with probability one, and is such that whether or not s> m depends solely on . In a sequential experiment E we observe the values where s is such a stopping rule and then stop. The restriction on the distribution of s means simply that whether or not you decide to stop cannot depend on future observations (unless you are clairvoyant), but only on the ones you have available to date.

7.2.2 Examples

1. Fixed sample size from a sequence of Bernoulli trials. Suppose that the xi are independently 1 with probability (representing ‘success’) or 0 with probability (representing ‘failure’). If s=n where n is a constant, then we have the usual situation which gives rise to the binomial distribution for the total number of successes.

2. Stopping after the first success in Bernoulli trials. With the xi as in the previous example, we could stop after the first success, so that

Because the probability that s> n is which tends to 0 as , this is finite with probability 1.

3. A compromise between the first two examples. With the xi as in the previous two examples. we could stop after the first success if that occurs at or before the nth trial, but if there has not been a success by then, stop at the nth trial, so that

4. Fixed size sample from the normal distribution. If the xi are independently and s=n where n is a constant, then we have a case which has arisen often before of a sample of fixed size from a normal distribution.

5. Stopping when a fixed number of standard deviations from the mean. Still taking , we could have

which, as , means stopping as soon as we observe a value of that is at least c standard deviations from the mean. It is not obvious in this case that s is finite with probability 1, but it follows from the law of the iterated logarithm, a proof of which can be found in any standard text on probability.

7.2.3 The stopping rule principle

The stopping rule principle is that in a sequential experiment, if the observed value of the stopping rule is m, then the evidence provided by the experiment about the value of θ should not depend on the stopping rule.

Before deciding whether it is valid, we must consider what it means. It asserts, for example, that if you observe ten Bernoulli trials, nine of which result in failure and only the last in success, then any inference about the probability of successes cannot depend on whether the experimenter had all along intended to carry out ten trials and had, in fact, observed one success, or whether he or she had intended to stop the experiment immediately the first success was observed. Thus, it amounts to an assertion that all that matters is what actually happened and not the intentions of the experimenter if something else had happened.

Theorem 7.2 The stopping rule principle follows from the likelihood principle, and hence is a logical consequence of the Bayesian approach.

Proof. If the xi are discrete random variables, then it suffices to note that the likelihood

which clearly does not depend on the stopping rule. There are some slight complications in the continuous case, which are largely to do with measure theoretic complications, and in particular with events of probability zero, but a general proof from the so-called relative likelihood principle is more or less convincing; for details, see Berger and Wolpert (1988, Sections 3.4.3 and 4.2.6).

7.2.4 Discussion

The point about this is as follows. A classical statistician is supposed to choose the stopping rule before the experiment and then follow it exactly. In actual practice, the ideal is often not adhered to; an experiment can end because the data already looks good enough, or because there is no more time or money, and yet the experiment is often analyzed as if it had a fixed sample size. Although stopping for some reasons would be harmless, statisticians who stop ‘when the data looks good’, a process which is sometimes described as optional (or optimal) stopping, can produce serious errors if used in a classical analysis.

It is often argued that a single number which is a good representation of our knowledge of a parameter should be unbiased, that is, should be such that its expectation over repeated sampling should be equal to that parameter. Thus, if we have a sample of fixed size from a Bernoulli distribution [example (1), mentioned before], then , so that is in that sense a good estimator of . However, if the stopping rule in example (2) or that in example (3), is used, then the proportion will, on average, be more than . If, for example, we take example (3) with n = 2, then

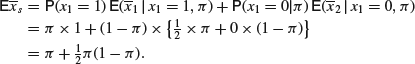
Thus, if a classical statistician who used the proportion of successes actually observed as an estimator of the probability of success, would be accused of ‘making the probability of success look larger than it is’.

The stopping rule principle also plays havoc with classical significance tests. A particular case can be constructed from example (5) above with, for example, c = 2. If a classical statistician were to consider data from an population in which (unknown to him or her) , then because s is so constructed that, necessarily, the value of is at least c standard deviations from the mean, a single sample of a fixed size equal to this would necessarily lead to a rejection of the null hypothesis that at the 5% level. By taking other values of c, it can be seen that a crafty classical statistician could arrange to reject a null hypothesis that was, in fact, true, at any desired significance level.

It can thus be seen that the stopping rule principle is very hard to accept from the point of view of classical statistics. It is for these reasons that Savage said that

I learned the stopping rule principle from Professor Barnard, in conversation in the summer of 1952. Frankly, I then thought it a scandal that anyone in the profession could advance an idea so patently wrong, even as today I can scarcely believe some people can resist an idea so patently right (Savage et al., 1962, p. 76).

From a Bayesian viewpoint, there is nothing to be said for unbiased estimates, while a test of a sharp null hypothesis would be carried out in quite a different way, and if (as is quite likely if in fact ) the sample size resulting in example (5) were very large, then the posterior probability that would remain quite large. It can thus be seen that if the stopping rule is seen to be plausible, and it is difficult to avoid it in view of the arguments for the likelihood principle in the last section, then Bayesian statisticians are not embarrassed in the way that classical statisticians are.