5.6 Comparison of two proportions; the $2 imes 2$ table

5.6.1 Methods based on the log-odds ratio

In this section, we are concerned with another two sample problem, but this time one arising from the binomial rather than the normal distribution. Suppose

and that we are interested in the relationship between π and ρ. Another way of describing this situation is in terms of a 2 × 2 table (sometimes called a 2 × 2 contingency table)

We shall suppose that the priors for π and ρ are such that and , independently of one another. It follows that the posteriors are also beta distributions, and more precisely if

then

We recall from Section 3.1 on the binomial distribution that if

then , so that

and similarly for . Now the z distribution is approximately normal (this is the reason that Fisher preferred to use the z distribution rather than the F distribution, which is not so near to normality), and so Λ and are approximately normal with these means and variances. Hence the log-odds ratio

is also approximately normal, that is,

or more approximately

If the Haldane reference priors are used, so that , then , , and , and so

The quantity ad/bc is sometimes called the cross-ratio, and there are good grounds for saying that any measure of association in the 2 × 2 table should be a function of the cross-ratio (cf. Edwards, 1963).

The log-odds ratio is a sensible measure of the degree to which the two populations are identical, and in particular if and only if . On the other hand, knowledge of the posterior distribution of the log-odds ratio does not in itself imply knowledge of the posterior distribution of the difference or the ratio . The approximation is likely to be reasonable provided that all of the entries in the table are at least 5.

5.6.2 Example

The table mentioned later [quoted from Di Raimondo (1951)] relates to the effect on mice of bacterial inoculum (Staphylococcus aureus). Two different types of injection were tried, a standard one and one with 0.15 U of penicillin per millilitre.

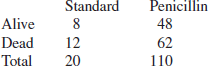
The cross-ratio is so its logarithm is –0.150 and a–1+b–1+c–1+d–1=0.245, and so the posterior distribution of the log odds-ratio is . Allowing for the s in the more exact form for the mean does not make much difference; in fact -0.150 becomes -0.169. The posterior probability that , that is, that the log odds ratio is positive, is

The data thus shows no great difference between the injections with and without the penicillin.

5.6.3 The inverse root-sine transformation

In Section 1.5 on ‘Means and variances’, we saw that if , then the transformation resulted in , say, and , and in fact it is approximately true that . This transformation was also mentioned in Section 3.2 on ‘Reference prior for the binomial likelihood’, and pointed out there that one of the possible reference priors for π was , and that this prior was equivalent to a uniform prior in . Now if we use such a prior, then clearly the posterior for ψ is approximately N(z,  1/4m), that is,

This is of no great use if there is only a single binomial variable, but when there are two it can be used to conclude that approximately

and so to give another approximation to the probability that . Thus with the same data as the above, radians, radians, and 1/4m+1/4n=0.0148, so that the posterior probability that is about . The two methods do not give precisely the same answer, but it should be borne in mind that the numbers are not very large, so the approximations involved are not very good, and also that we have assumed slightly different reference priors in deriving the two answers.

If there is non-trivial prior information, it can be incorporated in this method as well as in the previous method. The approximations involved are reasonably accurate provided that x(1–x/m) and y(1–y/n) are both at least 5.

5.6.4 Other methods

If all the entries in the 2 × 2 table are at least 10, then the posterior beta distributions are reasonably well approximated by normal distributions of the same means and variances. This is quite useful in that it gives rise to an approximation to the distribution of which is much more likely to be of interest than some function of π minus the same function of ρ. It will therefore allow us to give an approximate HDR for or to approximate the probability that lies in a particular interval.

In quite a different case, where the values of π and ρ are small, which will be reflected in small values of x/m and y/n, then the binomial distributions can be reasonably well approximated by Poisson distributions, which means that the posteriors of π and ρ are multiples of chi-squared distributions (cf. Section 3.4 on ‘The Poisson distribution’). It follows from this that the posterior of is a multiple of an F distribution (cf. Section 5.5). Again, this is quite useful because is a quantity of interest in itself. The Poisson approximation to the binomial is likely to be reasonable if n> 10 and either x/n< 0.05 or x/n> 0.95 (in the latter case, π has to be replaced by ).

The exact probability that can be worked out in terms of hypergeometric probabilities (cf. Altham, 1969), although the resulting expression is not usually useful for hand computation. It is even possible to give an expression for the posterior probability that (cf. Weisberg, 1972), but this is even more unwieldy.