5.5 Inferences concerning a variance ratio

5.5.1 Statement of the problem

In this section, we are concerned with the data of the same form as we met in the Behrens–Fisher problem. Thus say, we have independent vectors and such that

where all of are unknown. The difference is that in this case the quantity of interest is the ratio

of the two unknown variances, so that the intention is to discover how much more (or less) variable the one population is than the other. We shall use the same notation as before, and in addition we will find it useful to define

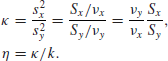
Again, we shall begin by assuming a reference prior

As was shown in Section 2.12 on ‘Normal mean and variance both unknown’, the posterior distributions of and ψ are independent and such that and so that

It turns out that has (Snedecor’s) F distribution on and degrees of freedom (or equivalently that its reciprocal has an F distribution on and degrees of freedom). The proof of this fact, which is not of great importance and can be omitted if you are prepared to take it for granted, is in Section 5.6.

The result is of the same type, although naturally the parameters are slightly different, if the priors for and ψ are from the conjugate family. Even if, by a fluke, we happened to know the means but not the variances, the only change would be an increase of 1 in each of the degrees of freedom.

5.5.2 Derivation of the F distribution

In order to find the distribution of κ, we need first to change variables to , noting that

It follows that

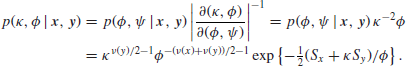
It is now easy enough to integrate out by substituting where and thus reducing the integral to a standard gamma function integral (cf. Section 2.12 on ‘Normal mean and variance both unknown’). Hence,

Defining k and as above, and noting that is constant, this density can be transformed to give

From Appendix A, it can be seen that this is an F distribution on and degrees of freedom, so that

Note that by symmetry

For most purposes, it suffices to think of an F distribution as being, by definition, the distribution of the ratio of two chi-squared (or inverse chi-squared) variables divided by their respective degrees of freedom.

5.5.3 Example

Jeffreys (1961, Section 5.4) quotes the following data (due to Lord Rayleigh) on the masses xi in grammes of m = 12 samples of nitrogen obtained from air (A) and the masses yi of n = 8 samples obtained by chemical method (C) within a given container at standard temperature and pressure.

It turns out that , , , , so that k=19/1902=0.010. Hence, the posterior of κ is such that

or equivalently

This makes it possible to give an interval in which we can be reasonably sure that the ratio κ of the variances lies. For reasons similar to those for which we chose to use intervals corresponding to HDRs for in Section 2.8 on ‘HDRs for the normal variance’, it seems sensible to use intervals corresponding to HDRs for log F. From the tables in the Appendix, such an interval of probability 90% for F11,7 is (0.32, 3.46), so that κ lies in the interval from 0.01/3.46 to 0.01/0.32, that is (0.003, 0.031), with a posterior probability of 90%. Because the distribution is markedly asymmetric, it may also be worth finding the mode of κ, which (from the mode of as given in Appendix A) is