5.4 The Behrens–Fisher controversy

5.4.1 The Behrens–Fisher problem from a classical standpoint

As pointed out in Section 2.6 on ‘Highest Density Regions’, in the case of a single normal observation of known variance there is a close relationship between classical results and Bayesian results using a reference prior, which can be summarized in terms of the ‘tilde’ notation by saying that, in classical statistics, results depend on saying that

while Bayesian results depend on saying that

As a result of this, if then the observation x = 5, say, leads to the same interval, , which is regarded as a 95% confidence interval for θ by classical statisticians and as a 95% HDR for θ by Bayesians (at least if they are using a reference prior). It is not hard to see that very similar relationships exist if we have a sample of size n and replace x by , and also when the variance is unknown (provided that the normal distribution is replaced by the t distribution).

There is also no great difficulty in dealing with the case of a two sample problem in which the variances are known. If they are unknown but equal (i.e. ), it was shown that if

then the posterior distribution of t is Student’s on degrees of freedom. A classical statistician would say that this ‘pivotal quantity’ has the same distribution whatever are, and so would be able to give confidence intervals for δ which were exactly the same as HDRs derived by a Bayesian statistician (always assuming that the latter used a reference prior).

This seems to suggest that there is always likely to be a way of interpreting classical results in Bayesian terms and vice versa, provided that a suitable prior distribution is used. One of the interesting aspects of the Behrens–Fisher problem is that no such correspondence exists in this case. To see why, recall that the Bayesian analysis led us to conclude that

where

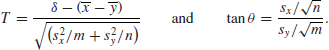
Moreover, changing the prior inside the conjugate family would only alter the parameters slightly, but would still give results of the same general character. So if there is to be a classical analogue to the Bayesian result, then if T is regarded as a function of the data and for fixed values of the parameters , it must have Behrens’ distribution over repeated samples and . There is an obvious difficulty in this, in that the parameter θ depends on the samples, whereas there is no such parameter in the normal or t distributions. However, it is still possible to investigate whether the sampling distribution of T depends on the parameters .

It turns out that its distribution over-repeated sampling does not just depend on the sample sizes m and n – it also depends on the ratio (which is not, in general, known to the statistician). It is easiest to see this when m = n and so (say). We first suppose that (unknown to the statistician) it is in fact the case that . Then the sampling distribution found in Section 5.2, for the case where the statistician did happen to know that must still hold (his or her ignorance can scarcely affect what happens in repeated sampling). Because if m = n then

in the notation of Section 5.2, it follows that

On the other hand if , then necessarily Sy=0 and so s2y=0, and hence . Since it must also be the case that and so , the distribution of T is given by

that is, T has a t distribution on degrees of freedom. For intermediate values of the distribution over repeated samples is intermediate between these forms (but is not, in general, a t distribution).

5.4.2 Example

Bartlett (1936) quotes an experiment in which the yields xi (in pounds per acre) on m plots for early hay were compared with the yields yi for ordinary hay on another n plots. It turned out that m=n=7 (so ), , , s2x=308.6, s2y=1251.3. It follows that , and so that radians. The Bayesian analysis now proceeds by saying that . By interpolation in tables of Behrens’ distribution a 50% HDR for δ is , that is, (28.6, 51.0). [Using the program in Appendix C we find that hbehrens(0.5,6,6,26) is the interval (–0.7452094,  0.7452094).]

A classical statistician who was willing to assume that would use tables of t12 to conclude that a 50% confidence interval was , that is, (29.4, 50.2). This interval is different, although not very much so, from the Bayesian’s HDR. Without some assumption such as he or she would not be able to give any exact answer.

5.4.3 The controversy

The Bayesian solution was championed by Fisher (1935, 1937, 1939). Fisher had his own theory of fiducial inference which does not have many adherents nowadays, and did not in fact support the Bayesian arguments put forward here. In an introduction to Fisher (1939) reprinted in his Collected Papers, Fisher said that

Pearson and Neyman have laid it down axiomatically that the level of significance of a test must be equal to the frequency of a wrong decision ‘in repeated samples from the same population’. The idea was foreign to the development of tests of significance given by the author in [Statistical Methods for Research Workers], for the experimenter’s experience does not consist in repeated samples from the same population, although in simple cases the numerical values are often the same; and it was, I believe, this coincidence which misled Pearson and Neyman, who were not very familiar with the ideas of ‘Student’ and the author.

Although Fisher was not a Bayesian, the above quotation does put one of the objections which any Bayesian must have to classical tests of significance.

In practice, classical statisticians can at least give intervals which, while they may not have an exact significance level, have a significance level between two reasonably close bounds. A recent review of the problem is given by Robinson (1976, 1982).