3.12 Exercises on Chapter 3
1. Laplace claimed that the probability that an event which has occurred n times, and has not hitherto failed, will occur again is (n+1)/(n+2) [see Laplace (1774)], which is sometimes known as Laplace’s rule of succession. Suggest grounds for this assertion.
2. Find a suitable interval of 90% posterior probability to quote in a case when your posterior distribution for an unknown parameter π is Be(20, 12), and compare this interval with similar intervals for the cases of Be(20.5, 12.5) and Be(21, 13) posteriors. Comment on the relevance of the results to the choice of a reference prior for the binomial distribution.
3. Suppose that your prior beliefs about the probability π of success in Bernoulli trials have mean 1/3 and variance 1/32. Give a 95% posterior HDR for π given that you have observed 8 successes in 20 trials.
4. Suppose that you have a prior distribution for the probability π of success in a certain kind of gambling game which has mean 0.4, and that you regard your prior information as equivalent to 12 trials. You then play the game 25 times and win 12 times. What is your posterior distribution for π?
5. Suppose that you are interested in the proportion of females in a certain organization and that as a first step in your investigation you intend to find out the sex of the first 11 members on the membership list. Before doing so, you have prior beliefs which you regard as equivalent to 25% of this data, and your prior beliefs suggest that a third of the membership is female.
Suggest a suitable prior distribution and find its standard deviation.
Suppose that 3 of the first 11 members turn out to be female; find your posterior distribution and give a 50% posterior HDR for this distribution.
Find the mean, median and mode of the posterior distribution.
Would it surprise you to learn that in fact 86 of the total number of 433 members are female?
Suggest a suitable prior distribution and find its standard deviation.
Suppose that 3 of the first 11 members turn out to be female; find your posterior distribution and give a 50% posterior HDR for this distribution.
Find the mean, median and mode of the posterior distribution.
Would it surprise you to learn that in fact 86 of the total number of 433 members are female?
6. Show that if 
then
then
Deduce that if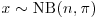 
has a negative binomial distribution of index n and parameter π and z=g(x) then 
and 
. What does this suggest as a reference prior for π?
has a negative binomial distribution of index n and parameter π and z=g(x) then and . What does this suggest as a reference prior for π?
7. The following data were collected by von Bortkiewicz (1898) on the number of men killed by horses in certain Prussian army corps in twenty years, the unit being one army corps for one year:
Give an interval in which the mean number λ of such deaths in a particular army corps in a particular year lies with 95% probability.
8. Recalculate the answer to the previous question assuming that you had a prior distribution for λ of mean 0.66 and standard deviation 0.115.
9. Find the Jeffreys prior for the parameter α of the Maxwell distribution
and find a transformation of this parameter in which the corresponding prior is uniform.
10. Use the two-dimensional version of Jeffreys’ rule to determine a prior for the trinomial distribution
(cf. Exercise 15 on Chapter 2).
11. Suppose that x has a Pareto distribution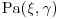
, where 
is known but γ is unknown, that is,
, where is known but γ is unknown, that is,
Use Jeffreys’ rule to find a suitable reference prior for γ.
12. Consider a uniform distribution on the interval 
, where the values of α and β are unknown, and suppose that the joint distribution of α and β is a bilateral bivariate Pareto distribution with 
. How large a random sample must be taken from the uniform distribution in order that the coefficient of variation (that is, the standard deviation divided by the mean) of the length 
of the interval should be reduced to 0.01 or less?
, where the values of α and β are unknown, and suppose that the joint distribution of α and β is a bilateral bivariate Pareto distribution with . How large a random sample must be taken from the uniform distribution in order that the coefficient of variation (that is, the standard deviation divided by the mean) of the length of the interval should be reduced to 0.01 or less?
13. Suppose that observations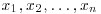 
are available from a density
are available from a density
Explain how you would make inferences about the parameter θ using a conjugate prior.
14. What could you conclude if you observed two tramcars numbered, say, 71 and 100?
15. In Section 3.8, we discussed Newcomb’s observation that the front pages of a well-used table of logarithms tend to get dirtier than the back pages do. What if we had an antilogarithm table, that is, a table giving the value of x when log10x is given? Which pages of such a table would be the dirtiest?
16. We sometimes investigate distributions on a circle (e.g. von Mises’ distribution which is discussed in Section 3.9 on ‘The circular normal distribution’). Find a Haar prior for a location parameter on the circle (such as μ in the case of von Mises’ distribution).
17. Suppose that the prior distribution 
for the parameters μ and σ of a Cauchy distribution
for the parameters μ and σ of a Cauchy distribution
is uniform in μ and σ, and that two observations x1=2 and x2=6 are available from this distribution. Calculate the value of the posterior density 
(ignoring the factor 
) to two decimal places for 
and 
. Use Simpson’s rule to approximate the posterior marginal density of μ, and hence go on to find an approximation to the posterior probability that 
.
(ignoring the factor 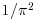) to two decimal places for 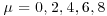and 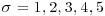. Use Simpson’s rule to approximate the posterior marginal density of μ, and hence go on to find an approximation to the posterior probability that .
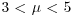18. Show that if the log-likelihood 
is a concave function of θ for each scalar x (that is, 
for all θ), then the likelihood function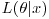 
for θ given an n-sample 
has a unique maximum. Prove that this is the case if the observations xi come from a logistic density
is a concave function of θ for each scalar x (that is, for all θ), then the likelihood function for θ given an n-sample has a unique maximum. Prove that this is the case if the observations xi come from a logistic density
where θ is an unknown real parameter. Fill in the details of the Newton–Raphson method and the method of scoring for finding the position of the maximum, and suggest a suitable starting point for the algorithms.
[In many applications of Gibbs sampling, which we consider later in Section 9.4, all full conditional densities are log-concave (see Gilks et al., 1996, Section 5.3.3), so the study of such densities is of real interest.]
19. Show that if an experiment consists of two observations, then the total information it provides is the information provided by one observation plus the mean amount provided by the second given the first.
20. Find the entropy 
of a (negative) exponential distribution with density 
.
of a (negative) exponential distribution with density .
1. Sometimes denoted DKL(1||2) or KL(1||2).
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.