3.6 Reference prior for the uniform distribution

3.6.1 Lower limit of the interval fixed

If consists of independent random variables with distributions, then

where , so that the likelihood can be written in the form

after multiplying by a constant (as far as θ is concerned). Hence,

with

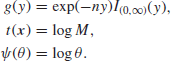
It follows that the likelihood is data translated, and the general argument about data translated likelihoods in Section 2.5 now suggests that we take a prior which is at least locally uniform in , that is . In terms of the parameter θ, the usual change of variable rule shows that this means

which is the same prior that is conventionally used for variances. This is not a coincidence, but represents the fact that both are measures of spread (strictly, the standard deviation is more closely analogous to θ in this case, but a prior for the variance proportional to the reciprocal of the variance corresponds to a prior for the standard deviation proportional to the reciprocal of the standard deviation). As the density of is proportional to , the density proportional to can be regarded as the limit Pa(0, 0) of as and . Certainly, if the likelihood is , then the posterior is Pa(M, n) which is what would be expected when the general rule is applied to the particular case of a Pa(0, 0) prior.

3.6.2 Example

A very artificial example can be obtained by taking groups of random digits from Neave (1978, Table 7.1) ignoring all values greater than some value θ [an alternative source of random digits is Lindley and Scott (1995, Table 27)]. A sample of 10 such values is:

This sample was constructed this sample using the value , but we want to investigate how far this method succeeds in giving information about θ, so we note that the posterior is Pa(0.620 58, 10). Since the density function of a Pareto distribution decreases monotonically beyond , an HDR must be of the form for some x, and since the distribution function is (see Appendix A)

a 90% HDR for θ is (0.620 58, x) where x is such that

and so is 0.781 26. Thus, a 90% HDR for θ is the interval (0.62, 0.78). We can see that the true value of θ in this artificial example does turn out to lie in the 90% HDR.

3.6.3 Both limits unknown

In the two parameter case, when where are both unknown and x is any one of the observations, note that it is easily shown that

Very similar arguments to those used in the case of the normal distribution with mean and variance both unknown in Section 2.12 can now be deployed to suggest independent priors uniform in θ and , so that

But

so that this corresponds to

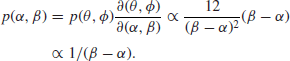
It may be noted that the density of is proportional to

so that in some sense a density

might be regarded as a limit of as and . Integrating over a uniform prior for , which might well seem reasonable, gives

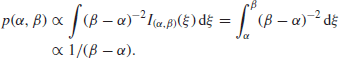
If the likelihood takes the form

then the posterior from this prior is Pabb(M, m, n–1). Thus, our reference prior could be regarded as a distribution, and if we think of it as such, the same formulae as before can be used.

The rule or corresponds to which is the prior Jeffreys’ rule gave us in the normal case with both parameters unknown (see Section 3.3 on Jeffreys’ rule).