3.5 The uniform distribution

3.5.1 Preliminary definitions

The support of a density is defined as the set of values of x for which it is non-zero. A simple example of a family of densities in which the support depends on the unknown parameter is the family of uniform distributions (defined later). While problems involving the uniform distribution do not arise all that often in practice, it is worth while seeing what complications can arise in cases where the support does depend on the unknown parameter.

It is useful to begin with a few definitions. The indicator function of any set A is defined by

This is sometimes called the characteristic function of the set A in some other branches of mathematics, but not in probability and statistics (where the term characteristic function is applied to the Fourier–Stieltjes transform of the distribution function).

We say that y has a Pareto distribution with parameters and γ and write

if it has density

This distribution is often used as a model for distributions of income. A survey of its properties and applications can be found in Arnold (1983).

We say that x has a uniform distribution (or a rectangular distribution) on and write

if it has density

so that all values in the interval are equally likely.

3.5.2 Uniform distribution with a fixed lower endpoint

Now suppose we have n independent observations such that

for each i, where θ is a single unknown parameter. Then

It is now easy to see that we can write the likelihood as

Defining

it is clear that

Because the likelihood depends on the data through M alone, it follows that M is sufficient for θ given .

It is now possible to see that the Pareto distribution provides the conjugate prior for the above likelihood. For if θ has prior

then the posterior is

If now we write

so that if and only if and , and hence

we see that

It follows that if the prior is then the posterior is and hence that the Pareto distribution does indeed provide the conjugate family. We should note that neither the uniform nor the Pareto distribution falls into the exponential family, so that we are not here employing the unambiguous definition of conjugacy given in Section 2.11 on ‘The exponential family’. Although this means that the cautionary remarks of Diaconis and Ylvisaker (1979 and 1985) (quoted in Section 2.10 on conjugate prior distributions) apply, there is no doubt of the ‘naturalness’ of the Pareto distribution in this context.

3.5.3 The general uniform distribution

The case where both parameters of a uniform distribution are unknown is less important, but it can be dealt with similarly. In this case, it turns out that an appropriate family of conjugate prior distributions is given by the bilateral bivariate Pareto distribution. We say that the ordered pair (y, z) has such a distribution and write

if the joint density is

Now suppose we have n independent observations such that

where α and β are unknown. Then

Defining

it is clear that the likelihood can be written as

Because the likelihood depends on the data through m and M alone, it follows that (m, M) is sufficient for given .

It is now possible to see that the bilateral bivariate Pareto distribution provides the conjugate prior for the aforementioned likelihood. For if has prior

then the posterior is

If now we write

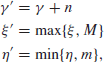
we see that

It follows that if the prior is then the posterior is and hence that the bilateral bivariate Pareto distribution does indeed provide the conjugate prior.

The properties of this and of the ordinary Pareto distribution are, as usual, described in Appendix A.

3.5.4 Examples

I realize that the case of the uniform distribution, and in particular the case of a uniform distribution on , must be of considerable importance, since it is considered in virtually all the standard text books on statistics. Strangely, however, none of the standard references seems to be able to find any reasonably plausible practical case in which it arises [with apologies to DeGroot (1970, Section 9.7) if his case really does arise]. In the circumstances, consideration of examples is deferred until Section 3.6, and even then the example considered will be artificial.