1.6 Exercises on Chapter 1
1. A card came is played with 52 cards divided equally between four players, North, South, East and West, all arrangements being equally likely. Thirteen of the cards are referred to as trumps. If you know that North and South have ten trumps between them, what is the probability that all three remaining trumps are in the same hand? If it is known that the king of trumps is included among the other three, what is the probability that one player has the king and the other the remaining two trumps?
2.
a. Under what circumstances is an event A independent of itself?
b. By considering events concerned with independent tosses of a red die and a blue die, or otherwise. give examples of events A, B and C which are not independent, but nevertheless are such that every pair of them is independent.
c. By considering events concerned with three independent tosses of a coin and supposing that A and B both represent tossing a head on the first trial, give examples of events A, B and C which are such that  although no pair of them is independent.
although no pair of them is independent.
3. Whether certain mice are black or brown depends on a pair of genes, each of which is either or . If both members of the pair are alike, the mouse is said to be homozygous, and if they are different it is said to be heterozygous. The mouse is brown only it it is homozygous . The offspring of a pair of mice have two such genes, one from each parent, and if the parent is heterozygous, the inherited gene is equally likely to be or . Suppose that a black mouse results from a mating between two heterozygotes.
a. What are the probabilities that this mouse is homozygous and that it is heterozygous?
Now suppose that this mouse is mated with a brown mouse, resulting in seven offspring, all of which turn out to be black.
b. Use Bayes’ Theorem to find the probability that the black mouse was homozygous BB.
c. Recalculate the same probability by regarding the seven offspring as seven observations made sequentially, treating the posterior after each observation as the prior for the next (cf. Fisher, 1959, Section II.2).
4. The example on Bayes’ Theorem in Section 1.2 concerning the biology of twins was based on the assumption that births of boys and girls occur equally frequently, and yet it has been known for a very long time that fewer girls are born than boys (cf. Arbuthnot, 1710). Suppose that the probability of a girl is p, so that
![]()
Find the proportion of monozygotic twins in the whole population of twins in terms of p and the sex distribution among all twins.
5. Suppose a red and a blue die are tossed. Let x be the sum of the number showing on the red die and twice the number showing on the blue die. Find the density function and the distribution function of x.
6. Suppose that  where n is large and π is small but
where n is large and π is small but  has an intermediate value. Use the exponential limit
has an intermediate value. Use the exponential limit 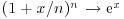 to show that
to show that 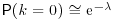 and
and 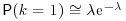 . Extend this result to show that k is such that
. Extend this result to show that k is such that
![]()
that is, k is approximately distributed as a Poisson variable of mean λ (cf. Appendix A).
7. Suppose that and have independent Poisson distributions of means and respectively (see question 6) and that .
a. Show that 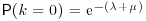 and
and  .
.
b. Generalize by showing that k has a Poisson distribution of mean  .
.
c. Show that conditional on k, the distribution of m is binomial of index k and parameter  .
.
8. Modify the formula for the density of a one-to-one function g(x) of a random variable x to find an expression for the density of x2 in terms of that of x, in both the continuous and discrete case. Hence, show that the square of a standard normal density has a chi-squared density on one degree of freedom as defined in Appendix A.
9. Suppose that  are independently and all have the same continuous distribution, with density f(x) and distribution function f(x). Find the distribution functions of
are independently and all have the same continuous distribution, with density f(x) and distribution function f(x). Find the distribution functions of
![]()
in terms of f(x), and so find expressions for the density functions of M and m.
10. Suppose that u and v are independently uniformly distributed on the interval [0, 1], so that the divide the interval into three sub-intervals. Find the joint density function of the lengths of the first two sub-intervals.
11. Show that two continuous random variables x and y are independent (i.e. p(x, y)=p(x)p(y) for all x and y) if and only if their joint distribution function F(x, y) satisfies F(x, y)=F(x)F(y) for all x and y. Prove that the same thing is true for discrete random variables. [This is an example of a result which is easier to prove in the continuous case.]
12. Suppose that the random variable x has a negative binomial distribution 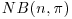 of index n and parameter π, so that
of index n and parameter π, so that
![]()
Find the mean and variance of x and check that your answer agrees with that given in Appendix A.
13. A random variable X is said to have a chi-squared distribution on 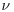 degrees of freedom if it has the same distribution as
degrees of freedom if it has the same distribution as
![]()
where Z1, Z2, 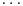 ,
,  are independent standard normal variates. Use the facts that
are independent standard normal variates. Use the facts that 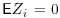 ,
, 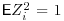 and
and  to find the mean and variance of X. Confirm these values using the probability density of X, which is
to find the mean and variance of X. Confirm these values using the probability density of X, which is
![]()
(see Appendix A).
14. The skewness of a random variable x is defined as 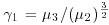 where
where
![]()
(but note that some authors work in terms of 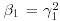 ). Find the skewness of a random variable X with a binomial distribution
). Find the skewness of a random variable X with a binomial distribution 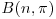 of index n and parameter π.
of index n and parameter π.
15. Suppose that a continuous random variable X has mean μ and variance  . By writing
. By writing
![]()
and using a lower bound for the integrand in the latter integral, prove that
![]()
Show that the result also holds for discrete random variables. [This result is known as Čebyšev’s Inequality (the name is spelt in many other ways, including Chebyshev and Tchebycheff).]
16. Suppose that x and y are such that
![]()
Show that x and y are uncorrelated but that they are not independent.
17. Let x and y have a bivariate normal distribution and suppose that x and y both have mean 0 and variance 1, so that their marginal distributions are standard normal and their joint density is
![]()
Show that if the correlation coefficient between x and y is ρ, then that between x2 and y2 is  .
.
18. Suppose that has a Poisson distribution (see question 6) of mean and that, for given , has a binomial distribution of index and parameter .
a. Show that the unconditional distribution of y is Poisson of mean
![]()
b. Verify that the formula
![]()
derived in Section 1.5 holds in this case.
19. Define
![]()
and show (by setting z=xy and then substituting z for y) that
![]()
Deduce that
![]()
By substituting (1+x2)z2=2t, so that  show that
show that 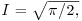 so that the density of the standard normal distribution as defined in Section 1.3 does integrate to unity and so is indeed a density. (This method is due to Laplace, 1812, Section 24.)
so that the density of the standard normal distribution as defined in Section 1.3 does integrate to unity and so is indeed a density. (This method is due to Laplace, 1812, Section 24.)
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
