1.5 Means and variances

1.5.1 Expectations

Suppose that m is a discrete random variable and that the series

is absolutely convergent, that is such that

Then the sum of the original series is called the mean or expectation of the random variable, and we denote it

A motivation for this definition is as follows. In a large number N of trials, we would expect the value m to occur about p(m)N times, so that the sum total of the values that would occur in these N trials (counted according to their multiplicity) would be about

so that the average value should be about

Thus, we can think of expectation as being, at least in some circumstances, a form of very long term average. On the other hand, there are circumstances in which it is difficult to believe in the possibility of arbitrarily large numbers of trials, so this interpretation is not always available. It can also be thought of as giving the position of the ‘centre of gravity’ of the distribution imagined as a distribution of mass spread along the x-axis.

More generally, if g(m) is a function of the random variable and is absolutely convergent, then its sum is the expectation of g(m). Similarly, if h(m, n) is a function of two random variables m and n and the series is absolutely convergent, then its sum is the expectation of h(m, n). These definitions are consistent in that if we consider g(m) and h(m, n) as random variables with densities of their own, then it is easily shown that we get these values for their expectations.

In the continuous case, we define the expectation of a random variable x by

provided that the integral is absolutely convergent, and more generally define the expectation of a function g(x) of x by

provided that the integral is absolutely convergent, and similarly for the expectation of a function h(x, y) of two random variables. Note that the formulae in the discrete and continuous cases are, as usual, identical except for the use of summation in the one case and integration in the other.

1.5.2 The expectation of a sum and of a product

If x and y are any two random variables, independent or not, and a, b and c are constants, then in the continuous case

and similarly in the discrete case. Yet more generally, if g(x) is a function of x and h(y) a function of y, then

We have already noted that the idea of independence is closely tied up with multiplication, and this is true when it comes to expectations as well. Thus, if x and y are independent, then

and more generally if g(x) and h(y) are functions of independent random variables x and y, then

1.5.3 Variance, precision and standard deviation

We often need a measure of how spread out a distribution is, and for most purposes the most useful such measure is the variance of x, defined by

Clearly if the distribution is very little spread out, then most values are close to one another and so close to their mean, so that is small with high probability and hence is small. Conversely, if the distribution is well spread out then is large. It is sometimes useful to refer to the reciprocal of the variance, which is called the precision. Further, because the variance is essentially quadratic, we sometimes work in terms of its positive square root, the standard deviation, especially in numerical work. It is often useful that

The notion of a variance is analogous to that of a moment of inertia in mechanics, and this formula corresponds to the parallel axes theorem in mechanics. This analogy seldom carries much weight nowadays, because so many of those studying statistics took it up with the purpose of avoiding mechanics.

In discrete cases, it is sometimes useful that

1.5.4 Examples

As an example, suppose that . Then

After a little manipulation, this can be expressed as

Because the sum is a sum of binomial probabilities, this expression reduces to , and so

Similarly,

and so

For a second example, suppose . Then

The integrand in the last expression is an odd function of and so vanishes, so that

Moreover,

so that on writing

Integrating by parts (using z as the part to differentiate), we get

1.5.5 Variance of a sum; covariance and correlation

Sometimes we need to find the variance of a sum of random variables. To do this, note that

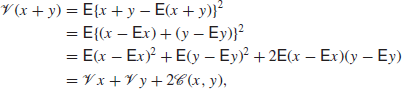
where the covariance of x and y is defined by

More generally,

for any constants a, b and c. By considering this expression as a quadratic in a for fixed b or vice versa and noting that (because its value is always positive) this quadratic cannot have two unequal real roots, we see that

We define the correlation coefficient between x and y by

It follows that

and indeed a little further thought shows that if and only if

with probability 1 for some constants a, b and c with a and b having opposite signs, while if and only if the same thing happens except that a and b have the same sign. If we say that x and y are uncorrelated.

It is easily seen that if x and y are independent then

from which it follows that independent random variables are uncorrelated.

The converse is not in general true, but it can be shown that if x and y have a bivariate normal distribution (as described in Appendix A), then they are independent if and only if they are uncorrelated.

It should be noted that if x and y are uncorrelated, and in particular if they are independent

(observe that there is a plus sign on the right-hand side even if there is a minus sign on the left).

1.5.6 Approximations to the mean and variance of a function of a random variable

Very occasionally, it will be useful to have an approximation to the mean and variance of a function of a random variable. Suppose that

Then if g is a reasonably smooth function and x is not too far from its expectation, Taylor’s theorem implies that

It, therefore, seems reasonable that a fair approximation to the expectation of z is given by

and if this is so, then a reasonable approximation to may well be given by

As an example, suppose that

and that z=g(x), where

so that

and thus . The aforementioned argument then implies that

The interesting thing about this transformation, which has a long history [see Eisenhart et al. (1947, Chapter 16) and Fisher (1954)], is that, to the extent to which the approximation is valid, the variance of z does not depend on the parameter π. It is accordingly known as a variance-stabilizing transformation. We will return to this transformation in Section 3.2 on the ‘Reference Prior for the Binomial Distribution’.

1.5.7 Conditional expectations and variances

If the reader wishes, the following may be omitted on a first reading and then returned to as needed.

We define the conditional expectation of y given x by

in the continuous case and by the corresponding sum in the discrete case. If we wish to be pedantic, it can occasionally be useful to indicate what we are averaging over by writing

just as we can write , but this is rarely necessary (though it can slightly clarify a proof on occasion). More generally, the conditional expectation of a function g(y) of y given x is

We can also define a conditional varianceas

Despite some notational complexity, this is easy enough to find since after all a conditional distribution is just a particular case of a probability distribution. If we are really pedantic, then is a real number which is a function of the real number x, while is a random variable which is a function of the random variable , which takes the value when takes the value x. However, the distinction, which is hard to grasp in the first place, is usually unimportant.

We may note that the formula

could be written as

but we must be careful that it is an expectation over values of (i.e. ) that occurs here.

Very occasionally we make use of results like

The proofs are possibly more confusing than helpful. They run as follows:

Similarly, we get the generalization

and in particular

hence

while

from which it follows that

1.5.8 Medians and modes

The mean is not the only measure of the centre of a distribution. We also need to consider the median from time to time, which is defined as any value x0 such that

In the case of most continuous random variables there is a unique median such that

We occasionally refer also to the mode, defined as that value at which the pdf is a maximum. One important use we shall have for the mode will be in methods for finding the median based on the approximation

or equivalently

(see the preliminary remarks in Appendix A).