Relation Variables
This chapter focuses on the logical difference between relation values (relations) and relation variables (relvars). In particular, it discusses and explains a variety of concepts and properties that are widely thought of as applying to relations as such but in fact don’t—they apply to relvars instead. The concepts in question include relational assignment (the well known shorthands INSERT, DELETE, and UPDATE in particular, also the less well known shorthands D_INSERT and I_DELETE); keys and foreign keys; key constraints, foreign key constraints, and other integrity constraints; The Golden Rule; and base vs. virtual relvars (views). The chapter concludes by defining and discussing the relational model as such.
Keywords
relation variable; relvar; relational assignment; key; foreign key; integrity constraint; the relational model
A golden key can open any door.
—late 16th century proverb
It’s an unfortunate fact that the term relation has long been used in the database literature—indeed, it still is used—to mean two quite different things. To be specific, it’s used to mean both a relation value and a relation variable. But there’s a clear logical difference here! What’s more, certain properties commonly thought of as properties of relation values—e.g., the property of having keys, and the property of possibly having foreign keys, and most especially the property of being updatable—are more correctly seen as properties of relation variables instead. This chapter elaborates on such matters.
Relations vs. Relvars
Consider the suppliers-and-shipments database from Fig. 1.1 once again. Now, what that figure clearly shows is two relation values: namely, the relation values that happen to appear in the database at some particular time. But, of course, if we were to look at the database at some different time, then we would probably see two different relation values. In other words, the objects referred to as S and SP in that figure are really variables: relation variables, to be precise, or in other words variables whose permitted values are relation values (different relation values at different times). For example, suppose relation variable S currently has the value shown in Fig. 1.1, and suppose we now delete the tuples for suppliers in Paris:
DELETE S WHERE CITY = 'Paris' ;
Here’s the result:
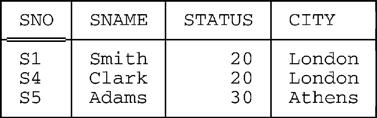
Conceptually, what’s happened here is that the old relation value of S has been replaced en bloc by an entirely new relation value. Of course, the old value (with five tuples) and the new one (with three) are somewhat similar, but they certainly are different values. Indeed, the DELETE operation just shown is basically shorthand for the following relational assignment:
S := S MINUS ( S WHERE CITY = 'Paris' ) ;
As in all assignments, what’s going on here, conceptually speaking, is that (a) the source expression on the right side is evaluated, and (b) the result of that evaluation is then assigned to the target variable on the left side.1 Thus, the net effect is, as already stated, to replace the “old” value of S by a “new” one, or in other words to update the variable S.2
In analogous fashion, of course, the relational INSERT and UPDATE operators are also just shorthand for certain relational assignments. In the case of INSERT, for example, the expression on the right side of that assignment represents the union of (a) the current value of the target relation variable and (b) a relation value containing the tuples to be inserted (see the section “Relational Assignment” for further discussion). Thus, while Tutorial D certainly does support the familiar INSERT, DELETE, and UPDATE operators on relation variables, it expressly recognizes that those operators are all just shorthand (albeit very convenient shorthand) for certain relational assignments.
Back to relation variables as such. Given the crucial importance of the logical difference between relation variables and relation values, we’ll take great care throughout this book to distinguish between the two. That is, we’ll be very careful to talk in terms of relation variables, not relation values, when it really is relation variables that we mean, and in terms of relation values, not relation variables, when it really is relation values that we mean. That said, however, we now add that—as previously noted in Chapter 1—we’ll abbreviate relation value, most of the time, to relation, unqualified (just as we abbreviate integer value most of the time to simply integer). And we’ll abbreviate relation variable most of the time to relvar; for example, we’ll say the suppliers-and-shipments database contains two relvars.3
Relvar Definitions
Here now, repeated from Chapter 1 for ease of reference, are the definitions of relvars S and SP from our running example:
VAR S BASE RELATION { SNO SNO , SNAME NAME , STATUS INTEGER , CITY CHAR }
KEY { SNO } ;VAR SP BASE RELATION { SNO SNO , PNO PNO ) KEY { SNO , PNO } FOREIGN KEY { SNO } REFERENCES S ;We remind you that any given relvar is declared to be of some specific relation type—and, of course, all possible values of that relvar (i.e., all relations that can possibly be assigned to that relvar) are of that same type, necessarily. For example, the type of both relvar S and all possible “supplier relations” is, precisely,
RELATION { SNO SNO , SNAME NAME, STATUS INTEGER , CITY CHAR }Also, the terms heading, body, attribute, tuple, cardinality, and degree, defined in Chapter 1 for relation values, can all be interpreted in the obvious way to apply to relation variables or relvars as well. (In the case of body, tuple, and cardinality, the terms must be understood as applying to the relation that happens to be the current value of the relvar in question.)
Furthermore, relvars, like relation values, also have a corresponding predicate (called the relvar predicate for the relvar in question): namely, the predicate that’s common to all of the relations that are possible values of the relvar in question. In the case of the suppliers relvar S, for example, the relvar predicate is (to repeat from Chapter 1):
Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY.
Finally, we remind you of The Closed World Assumption, which we discussed in Chapter 1 in connection with relations but in fact applies (perhaps more importantly) to relvars as well. Here again is the definition, but expressed now in terms of relvars rather than relations:
Definition: Let relvar R have predicate P. Then The Closed World Assumption (CWA) says: If tuple t appears in R at time T, then the instantiation p of P corresponding to t is assumed to be true at time T; conversely, if tuple t has the same heading as R but doesn’t appear in R at time T, then the instantiation p of P corresponding to t is assumed to be false at time T. In other words, a tuple appears in relvar R at a given time T if and only if it satisfies the predicate for R at that time T.
Relational Assignment
An explicit relational assignment as such takes the form:
R := rx
Here R is a relvar reference (syntactically, just a relvar name); rx is a relational expression; and the assignment works by assigning the relation r denoted by rx to the relvar R. Of course, r and R must be of the same relation type.
So now we can explain the syntax and semantics of the INSERT, DELETE, and UPDATE shorthands. First, however, we need to stress the point that these operators (as well as relational assignment), since they’re all update operators, aren’t operators of the relational algebra as such (recall from Chapter 2 that the operators of the relational algebra are all, by definition, read-only operators specifically). However, they can certainly be explained—in fact, they’re defined—in terms of such algebraic operators. For example, the INSERT statement
INSERT R rx ;
is shorthand for the following explicit relational assignment:
R := R UNION rx ;
Observe now that the foregoing definition of INSERT in terms of union implies that, other things being equal, an attempt to insert “a tuple that already exists”—i.e., an INSERT in which the relations denoted by R and rx aren’t disjoint—will succeed. (It won’t insert any duplicate tuples, of course—it just won’t have any effect as far as those existing tuples are concerned.) For such reasons, we define a variant on INSERT called D_INSERT (“disjoint INSERT”), with syntax as follows:
D_INSERT R rx ;
This statement is shorthand for:
R := R D_UNION rx ;
Recall from Chapter 2 that D_UNION—“disjoint union”—is just like regular union, except that it’s undefined if its operand relations have any tuples in common. It follows that an attempt to use D_INSERT to insert a tuple that already exists will fail (and an exception will be raised).
Turning now to DELETE, the DELETE statement
DELETE R rx ;
is shorthand for the following explicit assignment:
R := R MINUS rx ;
Note: The foregoing is the most general form of DELETE. But the DELETE example in the previous section—
DELETE S WHERE CITY = 'Paris' ;
—took the simpler form “DELETE R WHERE bx.” Now, that simpler form (which is actually the form most commonly encountered in practice) can be regarded as shorthand for a DELETE of the form “DELETE R rx” in which rx in turn takes the form “R WHERE bx”. However, an alternative and arguably simpler expansion for that common special form is:
R := R WHERE NOT ( bx )
Thus, we could alternatively say the DELETE in the example is shorthand for:
S := S WHERE NOT ( CITY = 'Paris' ) ;
We’ll be appealing to this alternative expansion from time to time in the chapters to come.
Now, the foregoing definition (i.e., of a DELETE of the form “DELETE R rx”) implies that, other things being equal, an attempt to delete “a tuple that doesn’t exist”—i.e., a DELETE in which the relation denoted by rx isn’t wholly included in the relation denoted by R—will succeed. For that reason, we define a variant on DELETE called I_DELETE (“included DELETE”), with syntax as follows:
I_DELETE R rx ;
This statement is shorthand for:
R := R I_MINUS rx ;
Recall from Chapter 2 that I_MINUS—“included minus”—is just like regular minus, except that it’s undefined if some tuple appears in its second operand relation and not in its first. It follows that an attempt to use I_DELETE to delete a tuple that doesn’t exist will fail, and an exception will be raised. (Note, however, that a DELETE of the form “DELETE R WHERE bx” can never attempt to delete “a tuple that doesn’t exist,” and no I_DELETE analog is needed in this case.)
As for UPDATE, the statement
UPDATE R WHERE bx : { A := ax } ;is shorthand for the following explicit assignment:
R := ( R WHERE NOT ( bx ) )
UNION
( EXTEND ( R WHERE bx ) : { A := ax } ) ;A here is, of course, an attribute reference—syntactically, just an attribute name—denoting an attribute of relvar R. As for the EXTEND in which that reference appears, note that it’s of the “what if” form (see Chapter 2 if you need to refresh your memory regarding this possibility).
Note: You might be wondering whether we could, or should, define a variant form of UPDATE, analogous to the D_INSERT and I_DELETE operators discussed above. For reasons beyond the scope of this book, however, such an operator doesn’t seem to make much sense.
Finally, we observe that assignment operations in general are required to satisfy what’s called The Assignment Principle. Here’s the definition:
Definition: The Assignment Principle states that after assignment of value v to variable V, the comparison v = V must evaluate to TRUE.
Of course, this principle actually applies to assignments of all kinds—in fact, as you can see, it’s more or less the definition of assignment—but for the purposes of this book it’s sufficient to note that it applies to relational assignments in particular.
Keys
Definition: Let K be a subset of the heading of relvar R. Then K is a key (also known as a candidate key) for R if and only if it possesses both of the following properties:
1. Uniqueness: No relation that can legally be assigned to R has two distinct tuples with the same value for K.
2. Irreducibility: No proper subset of K has the uniqueness property.
If K consists of n attributes, then n is the degree of K.
Note that every relvar does have at least one key (why?). Note too that keys are sets of attributes, not attributes per se (even when the set in question consists of just one attribute), because they’re defined to be a subset—not necessarily a proper subset—of the pertinent heading.4 Thus, the sole key for relvar S is {SNO} (note the braces), not SNO; likewise, the sole key for relvar SP is {SNO,PNO}. (In fact, as noted in Chapter 1, this latter relvar is “all key.”) In other words, relvar S is subject to the key constraint that {SNO} is a key for that relvar; likewise, relvar SP is subject to the key constraint that it’s all key.
By the way, observe that {SNAME} isn’t a key for relvar S, even though the SNAME values shown in Fig. 1.1 do happen to be unique. The point is, there’s no key constraint in effect that says supplier names have to be unique.
A remark on primary keys: If relvar R has more than one key (which is certainly possible), then it’s usual, though not required, to single out one of those keys and call it “primary.” And if relvar R has just one key, it’s also usual, but not required, to call that key “primary.” For reasons discussed in reference [43], we don’t insist on this practice; however, we don’t prohibit it either, and indeed we usually adopt it in our own examples. In particular, we assume, where it makes any difference, that {SNO} is the primary key for relvar S and {SNO,PNO} is the primary key for relvar SP. And in figures like Fig. 1.1, we adopt the convention of identifying primary keys by “double underlining” the attributes that constitute the key in question. Note, however, that Tutorial D actually has no syntax for distinguishing between primary and other keys. End of remark.
Functional Dependencies
Definition: Let X and Y be subsets of the heading of relvar R. Then the functional dependency X→Y holds in R if and only if, in every relation that’s a possible value of R, whenever two tuples have the same value for X, they also have the same value for Y.5
For example, suppose there’s a rule in effect in the suppliers-and-shipments world that says that if two suppliers are located in the same city at the same time, then they must have the same status at that time. Then the functional dependency (FD for short)
{ CITY } → { STATUS }would hold in relvar S. Note in particular that if K is a key for relvar R and Z is any subset of the heading of R, then the FD K→Z necessarily holds in R (why, exactly?)—in other words, every key constraint implies certain FD constraints, necessarily. See the section “Database Constraints” later in the chapter for further discussion of constraints in general.
Foreign Keys
In our running example, {SNO} in relvar SP is a foreign key, referencing the sole key {SNO} in relvar S. What this means is that if, at some given time T, relvar SP contains a tuple in which the SNO value is (let’s say) S3, then relvar S must contain a tuple at that same time T in which the SNO value is S3 as well. Here’s a definition:
Definition: Let relvars R2 and R1 (not necessarily distinct) be such that:
2. FK is a subset of the heading of R2.
3. At any given time, every FK value in R2 is required to be equal to the K value in some (necessarily unique) tuple in R1.6
Then FK is a foreign key in R2, referencing K in R1. And if FK consists of n attributes, then n is the degree of FK.
Actually the foregoing definition is considerably simplified, but it’s good enough for present purposes. Note, however, that it does tacitly assume that K and FK each consist of the very same attributes. That is (to spell the point out), every attribute in each of K and FK must have the same name and be of the same type as the corresponding attribute in the other; formally, in fact, they must be the very same attribute—which means that, in practice, the syntax for foreign key specifications might need to include some kind of support for attribute renaming (see, e.g., reference [42] for further discussion). Terminology:
■ Relvars R2 and R1 in the definition are the referencing relvar and the referenced (or target) relvar, respectively.
■ A particular tuple t2 in R2 and the corresponding tuple t1 in R1 are a referencing tuple and the corresponding referenced (or target) tuple, respectively.
■ Key K in R1 is the referenced (or target) key.
■ The constraint that, at any given time, every FK value in R2 is required to be equal to the K value in some tuple in R1 is a foreign key constraint or referential constraint.
■ The rule that no foreign key constraint must ever be violated is the referential integrity rule.
In our running example, any attempt to delete a supplier tuple must fail if it would otherwise leave any “dangling references”—i.e., references in relvar SP to the supplier tuple that now no longer exists.7
Database Constraints
A database constraint, or just a constraint for short,8 is, loosely, a boolean expression that (a) mentions no variables except database relvars and (b) must evaluate to TRUE (because if it evaluates to FALSE, there must be something wrong with the database). Any attempt to update the database in such a way as to cause some constraint to evaluate to FALSE must therefore fail—and, in the relational model, fail immediately, meaning an exception must be raised as soon as the update is attempted. Note: This requirement (i.e., that constraint violations be detected immediately) is sometimes called The Golden Rule. Observe that it’s a consequence of this rule that no user ever sees the database in an inconsistent state, where an inconsistent state is, by definition, a state of the database that violates at least one known constraint.
Of course, we’ve discussed key constraints and foreign key constraints (also functional dependencies) already. Such constraints are extremely important, but they’re also rather simple. Constraints of arbitrary complexity are possible, however, and do indeed occur in practice (sometimes they’re called business rules). Let’s consider a few examples:9
1. Supplier status values must be in the range 1 to 100 inclusive.
CONSTRAINT CX1 IS_EMPTY ( S WHERE STATUS < 1 OR STATUS > 100 ) ;
Alternatively:
CONSTRAINT CX1 AND ( S , STATUS ≥ 1 AND STATUS ≤ 100 ) ;
Explanation: AND here is an aggregate operator (we mentioned it in Chapter 2, but gave no examples there). It works on aggregates of boolean values, returning the logical AND of the boolean values in the aggregate in question.10 In the example, the aggregate contains one boolean value for each tuple in the suppliers relation, that value being computed by evaluating the boolean expression STATUS ≥ 1 AND STATUS ≤ 100 against the tuple in question. Note: When used in the context of a constraint, as in this example, AND might conveniently be pronounced “for all.” For example, the second formulation above of Constraint CX1 might intuitively be read as follows: “For all suppliers, the status must be greater than or equal to 1 and less than or equal to 100.”
2. Suppliers in London must have status 20.
CONSTRAINT CX2 IS_EMPTY ( S WHERE CITY = 'London' AND STATUS ≠ 20 ) ;
3. Supplier numbers must be unique.
CONSTRAINT CX3 COUNT ( S ) = COUNT ( S { SNO } ) ;
In other words, {SNO} is a key for relvar S. In practice, of course, we would almost certainly specify this constraint not by means of an explicit CONSTRAINT statement as shown, but rather by means of an appropriate KEY specification on the definition of relvar S. But it’s interesting to note that such a specification is really nothing more than shorthand for something that can be expressed, albeit more longwindedly, using that explicit CONSTRAINT syntax.
Aside: It would be more accurate to say Constraint CX3 means {SNO} is a superkey for relvar S. Loosely, a superkey is a superset—not necessarily a proper superset, of course—of a key; thus, all keys are superkeys, but “most” superkeys aren’t keys. Superkeys satisfy the key uniqueness requirement but not necessarily the key irreducibility requirement. In the case at hand, of course, the superkey in fact does satisfy the irreducibility requirement and is thus indeed a key after all. End of aside.
4. Suppliers with status less than 20 mustn’t supply part P6.
CONSTRAINT CX4
IS_EMPTY ( ( S JOIN SP ) WHERE STATUS < 20 AND PNO = PNO ( ‘P6’ ) ) ;
This constraint involves (better: interrelates) two distinct relvars, S and SP. In general, a constraint might involve, or interrelate, any number of distinct relvars. Terminology: A constraint that involves just a single relvar is known, informally, as a relvar constraint (sometimes a single-relvar constraint, for emphasis); a constraint that involves two or more distinct relvars is known, informally, as a multirelvar constraint. Constraints CX1-CX3 are all single-relvar constraints, while Constraint CX4 is a multirelvar constraint.
5. Every supplier number in SP must also appear in S.
CONSTRAINT CX5 SP { SNO } ⊆ S { SNO } ;
This example is also a multirelvar constraint, and what it means is that {SNO} in relvar SP is a foreign key, referencing relvar S. In practice, of course, we would almost certainly specify this constraint not by means of an explicit CONSTRAINT statement as shown, but rather by means of an appropriate FOREIGN KEY specification as part of the statement that defines relvar SP. But as with Example 3 above, it’s interesting to note that such a specification is really nothing more than shorthand11 for something that can be expressed using that explicit CONSTRAINT syntax.
Note finally that database constraints do apply specifically to relvars, not relations (which is why we discuss them in this chapter, of course). Why? Because, by definition, they constrain updates—that is, the only way they can be violated is by means of some update operation—and, again by definition, updates apply to variables, not values.
Multiple Assignment
Suppose the suppliers-and-shipments database is subject to a constraint to the effect that every supplier in London must be able to supply part P1:
CONSTRAINT CX6 IS_EMPTY
( ( S WHERE CITY = 'London' ) NOT MATCHING ( SP WHERE PNO = PNO ( 'P1' ) ) ) ;
Given this constraint, it’s clear that if we insert a new London supplier, say supplier number S6, into relvar S, then we also need to insert a shipment with supplier number S6 and part number P1 into relvar SP. The trouble is, if we try to do the INSERT on S first, it’ll fail on a violation of Constraint CX6, and if we try to do the INSERT on SP first, it’ll fail on a violation of Constraint CX5 (the foreign key constraint). So what we need to do is perform both updates at the same time, as it were—i.e., as a single combined operation. In other words, we need to perform a multiple assignment, like this:
INSERT S RELATION { TUPLE { SNO SNO ( 'S6' ) , … , CITY 'London' } } ,INSERT SP RELATION { TUPLE { SNO SNO ( 'S6' ) , PNO PNO ( 'P1' ) } } ;(Note the comma separator, which means the two INSERTs are part of the same overall statement.) Of course, INSERT is really assignment, so the foregoing “double INSERT” is really shorthand for a double assignment that, in outline, looks like this:
S := …, SP := … ;
This double assignment assigns one value to relvar S and another to relvar SP, both as part of the same overall operation. And—important!—no constraint checking is done until the end of the statement is reached (i.e., until the semicolon, in effect).
In outline, the semantics of multiple assignment are as follows: First, the source expressions on the right sides of the individual assignments are evaluated; second, those individual assignments are executed; last, any applicable constraints are checked. Observe in particular, therefore, that—precisely because the source expressions are all evaluated before any of the individual assignments are executed—none of those individual assignments can depend on the result of any other, and so the sequence in which they’re executed is irrelevant (you can think of them as being executed in parallel, or “simultaneously,” if you like).
Aside: The foregoing explanation requires some slight refinement in the case where two or more of the individual assignments specify the same target variable. In effect, what happens in such a situation (i.e., if two or more of the individual assignments do specify the same target variable) is that those particular assignments are executed in sequence as written. For further details, see reference [48]. End of aside.
Views
As noted in Chapter 2, the operators of the relational algebra are all read-only and thus apply, by definition, to relation values specifically. In particular, of course, they apply to the values that happen to be the current values of relation variables. As a consequence, it obviously makes sense to write an expression such as
S { SNO , CITY }and to read it as “the projection of relvar S on the SNO and CITY attributes”—meaning the projection on those attributes of the current value of relvar S (the result of that operation, of course, being a certain relation value).12 Occasionally, however, it’s convenient to use expressions like “the projection of relvar S on the SNO and CITY attributes” in a slightly different sense. In particular, we might want to define a view (also called a virtual relvar) SC of the suppliers relvar that consists of just the SNO and CITY attributes of that relvar, like this:
VAR SC VIRTUAL ( S { SNO , CITY } ) KEY { SNO } ;In this example, we might say, loosely but very conveniently, that relvar SC is “the projection on SNO and CITY of relvar S”—meaning, more precisely, that the value of relvar SC at any given time is the projection on SNO and CITY of the value of relvar S at the time in question. In a sense, therefore, we can talk in terms of projections of relvars per se, rather than just in terms of projections of current values of relvars. We hope this kind of dual usage on our part won’t cause you any confusion.
We’ll have comparatively little to say on the topic of views in this book; however, we should at least explain that from the user’s point of view—pardon the pun—views are supposed to behave just like base relvars. In fact, there’s another principle involved here:
Definition: The Principle of Interchangeability (of views and base relvars) states that there must be no arbitrary and unnecessary distinctions between base relvars and views; in other words, views should—as far as possible—“look and feel” just like base relvars as far as users are concerned.
See reference [44] for further discussion.
The Relational Model
We close this chapter with a formal, and deliberately somewhat terse, definition of the relational model, based on one given and discussed in detail in reference [45] and elsewhere. Here it is:
Definition: The relational model consists of five components:
1. An open ended collection of types, including type BOOLEAN in particular
2. A relation type generator and an intended interpretation for relations of types generated thereby
3. Facilities for defining relation variables of such generated relation types
4. A relational assignment operator for assigning relation values to such relation variables
5. A relationally complete, but otherwise open ended, collection of generic relational operators for deriving relation values from other relation values
The material of this chapter and its two predecessors should be sufficient to explain most if not all of the foregoing definition. If you need further clarification, please see reference [45].
Exercises
3.1 Write CONSTRAINT statements for the suppliers-and-shipments database to express the following requirements:
a. No Paris supplier can have status 20.
b. No two suppliers can be located in the same city.
c. At most one supplier can be located in Athens at any one time.
d. There must exist at least one London supplier.
e. The average supplier status must be at least 10.
f. No London supplier must be capable of supplying part P2.
3.2 With reference to the courses-and-students database from Exercise 2.2 in Chapter 2, write a constraint to express the fact that no student can be enrolled on a course prior to that course’s becoming available or prior to that student’s registration with the university.
Answers
a. CONSTRAINT CX31a IS_EMPTY ( S WHERE CITY = 'Paris' AND STATUS = 20 ) ;
b. CONSTRAINT CX31b COUNT ( S ) = COUNT ( S { CITY } ) ;
c. CONSTRAINT CX31c COUNT ( S WHERE CITY = 'Athens' ) < 2 ;
d. CONSTRAINT CX31d IS_NOT_EMPTY ( S WHERE CITY = 'London' ) ;
e. CONSTRAINT CX31e
CASE
WHEN IS_EMPTY ( S ) THEN TRUE
ELSE AVG ( S, STATUS ) ≥ 10
END CASE ;
f. CONSTRAINT CX31f IS_EMPTY ( ( S JOIN SP ) WHERE CITY = 'London' AND PNO = PNO ( 'P2' ) ) ;
3.2 CONSTRAINT CX32 IS_EMPTY ( JOIN { COURSE, STUDENT, ENROLLMENT } WHERE ENROLLED < AVAILABLE OR ENROLLED < REGISTERED ) ;
