9.6 The Metropolis–Hastings algorithm

9.6.1 Finding an invariant distribution

This whole section is largely based on the clear expository article by Chib and Greenberg (1995). A useful general review which covers Bayesian integration problems more generally can be found in Evans and Swartz (1995–1996; 2000).

A topic of major importance when studying the theory of Markov chains is the determination of conditions under which there exists a stationary distribution (sometimes called an invariant distribution), that is, a distribution such that

In the case where the state space is continuous, the sum is, of course, replaced by an integral.

In Markov Chain Monte Carlo methods, often abbreviated as MCMC methods, the opposite problem is encountered. In cases where such methods are to be used, we have a target distribution in mind from which we want to take samples, and we seek transition probabilities for which this target density is the invariant density. If we can find such probabilities, then we can start a Markov chain at an arbitrary starting point and let it run for a long time, after which the probability of being in state θ will be given by the target density .

It turns out to be useful to let be the probability that the chain remains in the same state and then to write

where while

Note that because the chain must go somewhere from its present position θ we have

for all θ. If the equation

is satisfied, we say that the probabilities satisfy time reversibility or detailed balance. This condition means that the probability of starting at θ and ending at when the initial probabilities are given by is the same as that of starting at and ending at θ. It turns out that when it is satisfied then gives a set of transition probabilities with as an invariant density. For

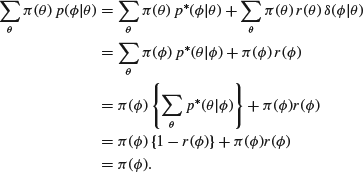
The result follows very similarly in cases where the state space is continuous.

The aforementioned proof shows that all we need to find the required transition probabilities is to find probabilities which are time reversible.

9.6.2 The Metropolis–Hastings algorithm

The Metropolis–Hastings algorithm begins by drawing from a candidate density as in rejection sampling, but, because we are considering Markov chains, the density depends on the current state of the process. We denote the candidate density by and we suppose that . If it turns out that the density q(y|x) is itself time reversible, then we need look no further. If, however, we find that

then it appears that the process moves from θ to too often and from to θ too rarely. We can reduce the number of moves from θ to by introducing a probability , called the probability of moving, that the move is made. In order to achieve time reversibility, we take to be such that the detailed balance equation

holds and consequently

We do not want to reduce the number of moves from to θ in such a case, so we take , and similarly in the case where the inequality is reversed and we have

It is clear that a general formula is

so that the probability of going from state θ to state is , while the probability that the chain remains in its present state θ is

The matrix of transition probabilities is thus given by

The aforementioned argument assumes that the state space is discrete, but this is just to make the formulae easier to take in – if the state space is continuous the same argument works with suitable adjustments, such as replacing sums by integrals.

Note that it suffices to know the target density up to a constant multiple, because it appears both in the numerator and in the denominator of the expression for . Further, if the candidate-generating density is symmetric, so that , the reduces to

This is the form which Metropolis et al. (1953) originally proposed, while the general form was proposed by Hastings (1970).

We can summarize the Metropolis–Hastings algorithm as follows:

1. Sample a candidate point from a proposal distribution1 .

2. Calculate

3. Generate a value which is uniformly distributed on (0, 1);

4. Then if we define ; otherwise we define

5. Return the sequence , , … , .

Of course we ignore the values of until the chain has converged to equilibrium. Unfortunately, it is a difficult matter to assess how many observations need to be ignored. One suggestion is that chains should be started from various widely separated starting points and the variation within and between the sampled draws compared; see Gelman and Rubin (1992). We shall not go further into this question; a useful reference is Gamerman and Lopes (2011, Section 5.4).

9.6.3 Choice of a candidate density

We need to specify a candidate density before a Markov chain to implement the Metropolis–Hastings algorithm. Quite a number of suggestions have been made, among them:

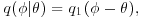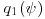• Random walk chains in which so that takes the form where has the density . The density is usually symmetric, so that , and in such cases the formula for the probability of moving reduces to

  

• Independence chains in which 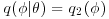does not depend on the current state θ. Although it sounds at first as if the transition probability does not depend on the current state θ, in fact it does through the probability of moving which is

  

  In cases where we are trying to sample from a posterior distribution, one possibility is to take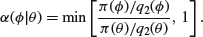 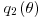to be the prior, so that the ratio becomes a ratio of likelihoods

  

  Note that there is no need to find the constant of proportionality in the posterior distribution.
• Autoregressive chains in which 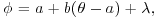where λ is random with density q3. It follows that 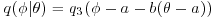. Setting b=–1 produces chains that are reflected about the point a and ensures negative correlation between successive elements of the chain.
• A Metropolis–Hastings acceptance–rejection algorithm due to Tierney (1994) is described by Chib and Greenberg (1995). We will not go into this algorithm here.

9.6.4 Example

Following Chib and Greenberg (1995), we illustrate the method by considering ways of simulating the bivariate normal distribution , where we take

If we define

so that (giving the Choleski factorization of ), it is easily seen that if we take

where the components of are independent standard normal variates, then has the required distribution, so that the distribution is easily simulated without using Markov chain Monte Carlo methods. Nevertheless, a simple illustration of the use of such methods is provided by this distribution. One possible set-up is provided by a random walk distribution , where the components Z1 and Z2 of are taken as independent uniformly distributed random variables with and and taking the probability of a move as

We can program this in as follows

n < - 600

mu < - c(1,2)

n < - 600

Sigma < - matrix(c(1,0.9,0.9,1),nr=2)

InvSigma < - solve(Sigma)

lik < - function(theta)opencurle 

    as.numeric(exp(-(theta-mu)\%*\%InvSigma\%*\%(theta-mu)/2))

closecurle 

alpha < - function(theta,phi) min(lik(phi)/lik(theta),1)

theta1 < - matrix(0,n,2)

theta1[1,] < - mu

k1 < - 0

for (i in 2:n)opencurle 

    theta < - theta1[i-1,]

    Z < - c(0.75,1) - c(1.5*runif(1),2*runif(1))

    phi < - theta + Z

    k < - rbinom(1,1,alpha(theta,phi))

    k1 < - k1 + k

    theta1[i,] < - theta + k*(phi-theta)

closecurle 

plot(theta1,xlim=c(-4,6),ylim=c(-3,7))}

An autoregressive chain can be constructed simply by replacing the line

phi < - theta + Z

by the line

phi < - mu - (theta - mu) + Z

and otherwise proceeding as before.

9.6.5 More realistic examples

A few further examples of the use of the Metropolis–Hastings algorithm areas follows:

• Carlin and Louis (2000, Example 5.7) consider the data on a number of flour beetles exposed to varying amounts of gaseous carbon disulphide (CS2) and attempt to fit a generalization (suggested by Prentice, 1976) of the logistic model we shall consider in Section 9.8.
• Chib and Greenberg (1994) consider an application to inference for regression models with ARMA(p, q) errors.
• Geman and Geman (1984) showed how the Metropolis algorithm can be used in image restoration, a topic later dealt with by Besag (1986).
• The algorithm can also be used to solve the ‘travelling salesman problem’. A nice web reference for this is

       http://hermetic.nofadz.com/misc/ts3/ts3demo.htm

9.6.6 Gibbs as a special case of Metropolis–Hastings

Gibbs sampling can be thought of as a special case of the Metropolis–Hastings algorithm in which all jumps from to are such that and differ only in one component. Moreover, if j is the component currently being updated and we write for the vector omitting the jth component, then, since we choose a value of from the density , it follows from the usual rules for conditional probability that

We can thus conclude that

is identically equal to unity. In this way, the Gibbs sampler emerges as a particular case of the Metropolis–Hastings algorithm in which every jump is accepted.

9.6.7 Metropolis within Gibbs

In the Gibbs sampler as we originally described it, the process always jumps in accordance with the transition probability . A modification, referred to as Metropolis within Gibbs or the Metropolized Gibbs sampler, is to sample a candidate point different from with probability

The value is then replaced by with probability

This modification is statistically more efficient, although slightly more complicated, than the usual Gibbs sampler; see Liu (1996, 2001). It is employed under certain circumstances by WinBUGS, which is described later.