4.5 Point null hypotheses for the normal distribution

4.5.1 Calculation of the Bayes’ factor

Suppose is a vector of independently random variables, and that is known. Because of the remarks at the end of the last section, we can work entirely in terms of the sufficient statistic

We have to make some assumption about the density of θ under the alternative hypothesis, and clearly one of the most natural things to do is to suppose that this density is normal, say . Strictly, this should be regarded as a density on values of θ other than , but when probabilities are found by integration of this density, the odd point will make no difference. It will usually seem sensible to take as, presumably, values near to are more likely than those far away, and this assumption will accordingly be made from now on. We note that the standard deviation of the density of θ under the alternative hypothesis is supposed to be considerably greater than the width of the interval of values of θ considered ‘indistinguishable’ from .

It is quite easy to find the predictive distribution of under the alternative, namely,

by writing

as in Section 2.2 on ‘Normal prior and likelihood’. Then because, independently of one another, and , the required density of is .

It follows that the Bayes factor B is

It is now useful to write

for the statistic used in classical tests of significance. With this definition

The posterior probability p0 can now be found in terms of the prior probability and the Bayes factor B by the usual formula

derived in Section 4.1 when we first met hypothesis tests.

4.5.2 Numerical examples

For example, if and , then the values

give rise to a Bayes factor

and hence to a posterior probability

This result is quite extraordinarily different from the conclusion that a classical statistician would arrive at with the same data. Such a person would say that, since z has a sampling distribution that is N(0, 1), a value of z that is, in modulus, 1.96 or greater would arise with probability only 5% (i.e. the two-tailed P-value of z=1.96 is 0.05), and consequently would reject the null hypothesis that at the 5% level. With the above assumptions about prior beliefs, we have, on the contrary, arrived at a posterior probability of 40% that the null hypothesis is true! Some further sample values are as follows (cf. Berger, 1985, Section 4.3):

The results of classical and Bayesian analyses differ more and more as the sample size . For fixed z, it is easy to see that B is asymptotically

and hence . Consequently, 1–p0 is of order and thus . So, with the specified prior, the result that z=1.96, which a classical statistician would regard as just sufficient to result in rejection of the null hypothesis at the 5% level irrespective of the value of n, can result in an arbitrarily high posterior probability p0 of the null hypothesis. Despite this, beginning users of statistical techniques often get the impression that if some data are significant at the 5% level then in some sense the null hypothesis has a probability after the event of at most 5%.

A specific example of a problem with a large sample size arises in connection with Weldon’s dice data, quoted by Fisher (1925b, Section 18 and Section 23). It transpired that when 12 dice were thrown 26 306 times, the mean and variance of the number of dice showing more than 4 were 4.0524 and 2.6983, as compared with a theoretical mean of for fair dice. Approximating the binomial distribution by a normal distribution leads to a z statistic of

The corresponding two-tailed P-value is approximately where is the density function of the standard normal distribution (cf. Abramowitz and Stegun, 1965, equation 26.2.12), so about 1 in 4 000 000. However, a Bayesian analysis (assuming and as usual) depends on a Bayes factor

and so to a posterior probability of 1 in 4000 that the dice were fair. This is small, but nevertheless the conclusion is not as startling as that which the classical analysis leads to.

4.5.3 Lindley’s paradox

This result is sometimes known as Lindley’s paradox (cf. Bartlett, 1957; Lindley, 1957; Shafer, 1982) and sometimes as Jeffreys’ paradox, because it was in essence known to Jeffreys (see Jeffreys, 1961, Section 5.2), although he did not refer to it as a paradox. A useful recent reference is Berger and Delempady (1987).

It does relate to something which has been noted by users of statistics. Lindley once pointed out (see Zellner, 1974, Section 3.7) that experienced workers often lament that for large sample sizes, say 5000, as encountered in survey data, use of the usual t-statistic and the 5% significance level shows that the values of parameters are usually different from zero and that many of them sense that with such a large sample the 5% level is not the right thing to use, but do not know what else to use (see also Jeffreys, 1961, Appendix B). On the other hand, in many scientific contexts, it is unrealistic to use a very large sample because systematic bias may vitiate it or the observer may tire [see Wilson (1952, Section 9.6) or Baird (1962, Section 2.8)].

Since the result is so different from that found by so many statisticians, it is important to check that it does not depend very precisely on the nature of the prior distribution which led to it.

We assumed that the prior probability of the null hypothesis was , and this assumption does seem ‘natural’ and could be said to be ‘objective’; in any case a slight change in the value of would not make much difference to the qualitative feel of the results.

We also assumed that the prior density of under the alternative hypothesis was normal of mean with some variance ψ. In fact, the precise choice of does not make a great deal of difference unless is large. Lindley (1957) took to be a uniform distribution

over an interval centred on , while Jeffreys (1961, Section 5.2) argues that it should be a Cauchy distribution,that is,

although his arguments are far from overwhelming and do not seem to have convinced anyone else. An examination of their work will show that in general terms they arrive at similar conclusions to those derived earlier.

There is also a scale parameter ψ in the distribution to be decided on (and this is true whether this distribution is normal, uniform or Cauchy). Although it seems reasonable that ψ should be chosen proportional to , there does not seem to be any convincing argument for choosing this to have any particular value (although Jeffreys tries to give a rational argument for the Cauchy form in general, he seems to have no argument for the choice of ψ beyond saying that it should be proportional to ). But it is easily seen that the effect of taking

on B and p0 is just the same as taking if n is multiplied by a factor k. It should be noted that it will not do to let and thus to take as a uniform distribution on the whole real line, because this is equivalent to multiplying n by a factor which tends to and so leads to and . It would clearly not be sensible to use a procedure which always gave the null hypothesis a posterior value of unity. In any case, as Jeffreys points out (1961, Section 5.0), ‘the mere fact that it has been suggested that [θ] is zero corresponds to some presumption that it is fairly small’.

4.5.4 A bound which does not depend on the prior distribution

In fact, it is possible to give a bound on B which does not depend on any assumptions about . We know that

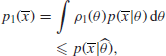
where is the maximum likelihood estimator of θ, that is,

In the case being considered, has a normal distribution of mean θ and hence , so that

It follows that the Bayes factor satisfies

so writing as before, we see that

implying a corresponding lower bound on p0. Some sample values (assuming that ) are as follows:

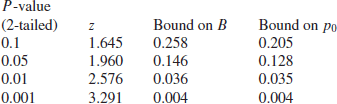
[cf. Berger, 1985, Section 4.3; Berger further claims that if and z> 1.68 then ]. Note that this bound does not depend on the sample size n and so does not demonstrate Lindley’s paradox.

As an example, if z=1.96 then the Bayes factor B is at least 0.146 and hence the posterior probability of the null hypothesis is at least 0.128. Unlike the results derived earlier assuming a more precise form for , the bounds no longer depend on the sample size, but it should be noted that the conclusion still does not accord at all well with the classical result of significance at the 5% level.

4.5.5 The case of an unknown variance

In the case where is unknown, similar conclusions follow, although there are a few more complications. It will do now harm if the rest of this section is ignored at a first reading (or even at a second).

We need first to find the density . If is unknown, then as was shown in Section 2.12 on ‘Normal mean and variance both unknown’

where . Using a reference prior for , it is easy to integrate out much as was done there to get

where and

It is now necessary to find the predictive density under the alternative hypothesis. To do this, first return to

Assuming a prior , we can integrate θ out; thus,

The last integral is of course proportional to , so to , while a little manipulation shows that

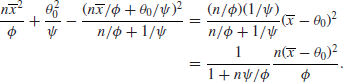
It follows that

To go any further, it is necessary to make some assumption about the relationship between and ψ. If it is assumed that

and a reference prior is used, then the predictive distribution under the alternative hypothesis becomes

where t is the same statistic encountered in the case of the null hypothesis. It follows that the Bayes factor is

and hence, it is possible to find p0 and p1.

It should be noted that as the exponential limit shows that the Bayes factor is asymptotically

which as is the same as in the known variance case.