4.4 Point (or sharp) null hypotheses with prior information

4.4.1 When are point null hypotheses reasonable?

As was mentioned in Section 4.3, it is very common in classical statistics to conduct a test of a point (or sharp) null hypothesis

In such a case, the full-scale Bayesian approach (as opposed to the compromise described in the previous section) gives rise to conclusions which differ radically from the classical answers.

Before getting on to the answers, a few basic comments about the whole problem are in order. First, tests of point null hypotheses are often performed in inappropriate circumstances. It will virtually never be the case that one seriously entertains the hypothesis that exactly, a point which classical statisticians fully admit (cf. Lehmann, 1986, Sections 4.5, 5.2). More reasonable would be the null hypothesis

where is so chosen that all can be considered ‘indistinguishable’ from . An example in which this might arise would be an attempt to analyze a chemical by observing some aspect, described by a parameter θ, of its reaction with a known chemical. If it were desired to test whether or not the unknown chemical was a specific compound, with a reaction strength known to an accuracy of ε, it would be reasonable to test

An example where ε might be extremely close to zero is a test for extra-sensory perception (ESP) with representing the hypothesis of no ESP. (The only reason that ε would probably not be zero here is that an experiment designed to test for ESP probably would not lead to a perfectly well-defined .) Of course, there are also many decision problems that would lead to a null hypothesis of the aforementioned form with a large ε, but such problems will rarely be well approximated by testing a point null hypothesis.

The question arises, if a realistic null hypothesis is H, when is it reasonable to approximate it by H? From a Bayesian viewpoint, it will be reasonable if and only when we spread the quantity p0 of prior probability over , the posterior probability is close to that of when a lump of prior probability p0 is concentrated on the single value . This will certainly happen if the likelihood function is approximately constant on , but this is a very strong condition, and one can often get away with less.

4.4.2 A case of nearly constant likelihood

Suppose that are independently where is known. Then we know from Section 2.3 on ‘Several normal observations with a normal prior’ that the likelihood is proportional to an density for θ. Now over the interval this likelihood varies by a factor

It follows that if we define z to be the statistic

used in classical tests of significance, and

then the likelihood varies over by a factor which is at most exp(2k). Hence, provided that ε is reasonably small, there is a useful bound on the variation of the likelihood.

For example, if ε can be taken to be 0.0025 and

then the likelihood varies by at most exp(2k) over . More specifically, if z = 2, and n = 25, then k becomes

and exp(2k)=1.05=1/0.95. In summary, if all values within of are regarded as indistinguishable from , then we can feel reassured that the likelihood function does not vary by more than 5% over this range of indistinguishable values, and if the interval can be made even smaller then the likelihood is even nearer to being constant.

Note that the bound depends on as well as on .

4.4.3 The Bayesian method for point null hypotheses

We shall now develop a theory for testing point null hypotheses, which can then be compared with the classical theory. If there is doubt as to the adequacy of the point null hypothesis as a representation of the real null hypothesis, it is always possible to test an interval null hypothesis directly by Bayesian methods and compare the results (and this will generally be easier than checking the constancy of the likelihood function).

You cannot use a continuous prior density to conduct a test of because that would of necessity give a prior probability of zero and hence a posterior probability of zero. A reasonable way of proceeding is to give a prior probability of and to assign a probability density to values where and integrates to unity. If you are thinking of the hypothesis as an approximation to a hypothesis then is really your prior probability for the whole interval .

You can then derive the predictive density of a vector of observations in the form

Writing

for what might be called the predictive distribution under the alternative hypothesis we see that

It follows that the posterior probabilities are

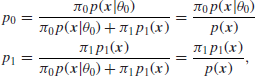
and so, the Bayes factor is

Of course, it is possible to find the posterior probabilities p0 and p1 in terms of the Bayes factor B and the prior probability as noted in Section 4.1 when hypothesis testing in general was discussed.

4.4.4 Sufficient statistics

Sometimes, we have a sufficient statistic for x given θ, so that

where is not a function of θ. Clearly in such a case,

so that we can cancel a common factor to get

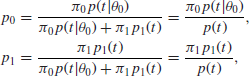
and the Bayes factor is

In short, x can be replaced by t in the formulas for p0, p1 and the Bayes factor B.

Many of the ideas in this section should become clearer when you come to look at Section 4.5, in which the particular case of the normal mean is explored in detail.