Acoustics

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5.2. Pressure-gradient microphones

A pressure-gradient microphone is one that responds to a difference in pressure at two closely spaced points. A common example of this type of microphone has a diaphragm, both sides of which are exposed to the sound wave. Such a construction is shown in Fig. 5.4.

Figure 5.4 Sketch of a pressure-gradient microphone consisting of a movable diaphragm, both sides exposed, connected to a transducing element.

If a pressure-gradient microphone is placed in the cavity of Fig. 5.2a, there will be no net force acting on the diaphragm and its output will be zero. This happens because there is no pressure gradient in the cavity. In contrast, if a pressure-gradient microphone is placed at the successive positions 1–4 of Fig. 5.3a, it will produce an output voltage proportional to the pressure gradient Δp/Δx. In other words, if Δx is the same between successive points, the microphone output will be independent of whichever of the four positions it occupies in Fig. 5.3a.

If a very small pressure-gradient microphone is placed in a plane sound wave traveling in the x direction, the complex force

{\tilde{f}}_{D}

${\tilde{f}}_{D}$

acting to move the diaphragm will be

{\tilde{f}}_{D} = - S \frac{\partial \tilde{p}}{\partial x} Δ l \cos θ

${\tilde{f}}_{D} = - S \frac{\partial \tilde{p}}{\partial x} Δ l \cos θ$

(5.1)

where

$\tilde{p}$ $\tilde{p}$ is sound pressure
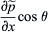$\frac{\partial \tilde{p}}{\partial x} \cos θ$ $\frac{\partial \tilde{p}}{\partial x} \cos θ$ is the component of the x gradient of pressure acting across the faces of the diaphragm
θ is the angle the normal to the diaphragm makes with the direction of travel of the wave (see Fig. 5.5)
Δl is the effective distance between the two sides of the diaphragm (see Fig. 5.4)
S is area of diaphragm.

The equation for a plane traveling sound wave has already been given (Eq. (2.121)); It is

\tilde{p} = {\tilde{p}}_{0} e^{- j k x}

$\tilde{p} = {\tilde{p}}_{0} e^{- j k x}$

(5.2)

where

k = ω/c
${\tilde{p}}_{o}$ ${\tilde{p}}_{o}$ is pressure at x = 0

If we assume that the introduction of the microphone into the sound field does not affect the pressure gradient, we may substitute Eq. (5.2) into Eq. (5.1) and get

{\tilde{f}}_{D} = \frac{j {\tilde{p}}_{0} ω S Δ l \cos θ}{c} e^{- j k x} .

${\tilde{f}}_{D} = \frac{j {\tilde{p}}_{0} ω S Δ l \cos θ}{c} e^{- j k x} .$

(5.3)

Figure 5.5 Pressure-gradient microphone with principal axis located at an angle θ with respect to the direction of travel of the sound wave.

The magnitude of the force at any point x is

| {\tilde{f}}_{D} | = \frac{| \tilde{p} | ω S Δ l \cos θ}{c} .

$| {\tilde{f}}_{D} | = \frac{| \tilde{p} | ω S Δ l \cos θ}{c} .$

(5.4)

It should be remembered (see Eq. (2.4)) that in the steady state the pressure gradient is proportional to jωρ ₀ times the component of particle velocity in the direction the gradient is being taken. The force f _D is therefore proportional to the particle velocity at any given frequency. A reference to Fig. 5.5 is sufficient to convince one that when θ = 90 degrees, the force acting on the diaphragm will be zero because the conditions of symmetry require that the pressure be the same on both sides of the diaphragm. From Eq. (5.4) we also see that the effective force acting on the diaphragm is proportional to frequency and the sound pressure.

In spherical coordinates, for a microphone whose dimensions are small compared with r, Eq. (5.1) becomes

{\tilde{f}}_{D} = - S \frac{\partial \tilde{p}}{\partial r} Δ l \cos θ .

${\tilde{f}}_{D} = - S \frac{\partial \tilde{p}}{\partial r} Δ l \cos θ .$

(5.5)

The equation for a spherical wave is found from Eq. (2.142)

\tilde{p} (r) = {\tilde{A}}_{0} \frac{e^{- j k r}}{r}

$\tilde{p} (r) = {\tilde{A}}_{0} \frac{e^{- j k r}}{r}$

(5.6)

Substituting (5.6) in (5.5) gives

{\tilde{f}}_{D} = \frac{{\tilde{A}}_{0} (1 + j k r)}{r^{2}} e^{- j k r} S (Δ l \cos θ) .

${\tilde{f}}_{D} = \frac{{\tilde{A}}_{0} (1 + j k r)}{r^{2}} e^{- j k r} S (Δ l \cos θ) .$

(5.7)

This yields

| {\tilde{f}}_{D} | rms = \frac{{| \tilde{p} |}_{rms} ω S Δ l \cos θ}{c} \cdot \frac{\sqrt{1 + k^{2} r^{2}}}{k r} .

$| {\tilde{f}}_{D} | rms = \frac{{| \tilde{p} |}_{rms} ω S Δ l \cos θ}{c} \cdot \frac{\sqrt{1 + k^{2} r^{2}}}{k r} .$

(5.8)

However, we see from Eq. (2.124) that in a plane wave the rms velocity is related to the rms pressure by

{| \tilde{u} |}_{rms} = \frac{{| \tilde{p} |}_{rms}}{ρ_{0} c}

${| \tilde{u} |}_{rms} = \frac{{| \tilde{p} |}_{rms}}{ρ_{0} c}$

(5.9)

and in a spherical wave (Eq. (2.144))

{| \tilde{u} |}_{rms} = \frac{{| \tilde{p} |}_{rms}}{ρ_{0} c} \frac{\sqrt{1 + k^{2} r^{2}}}{k r}

${| \tilde{u} |}_{rms} = \frac{{| \tilde{p} |}_{rms}}{ρ_{0} c} \frac{\sqrt{1 + k^{2} r^{2}}}{k r}$

(5.10)

where

{| \tilde{u} |}_{rms}

${| \tilde{u} |}_{rms}$

is the rms particle velocity in the direction of travel of the sound wave. Hence, Eqs. (5.4) and (5.8) become

{| {\tilde{f}}_{D} |}_{rms} = {| \tilde{u} |}_{rms} ω ρ_{0} S Δ l \cos θ .

${| {\tilde{f}}_{D} |}_{rms} = {| \tilde{u} |}_{rms} ω ρ_{0} S Δ l \cos θ .$

(5.11)

In other words, the effective (rms) force f _D acting on the diaphragm of a pressure-gradient microphone is directly proportional to the effective particle velocity in the direction of propagation of the wave, to the frequency, to the density of the air, to the size and area of the diaphragm, and to the angle it makes with the direction of propagation of the sound wave. This statement is true for any type of wave front—plane, spherical, cylindrical, or other—provided the microphone is so small that its presence does not appreciably disturb the sound wave.

At any given frequency, the response of the microphone is proportional to the cos θ, which yields the directivity pattern shown in Fig. 5.6a. This shape of plot is commonly referred to as a “figure of eight” pattern. The same pattern, plotted in decibels relative to the force at θ = 0, is given in Fig. 5.6b. It is interesting to observe that the pattern is the same as that for an acoustic doublet or for an unflanged diaphragm at low frequencies (see Fig. 4.23 and Fig. 13.23).

The frequency response of a pressure-gradient (particle-velocity) microphone, when placed in a spherical wave, is a function of the curvature of the wave front. That is to say, from Eq. (5.10) we see that for values of k ² r ² (kr equals ωr/c) large compared with 1 the particle velocity is linearly related to the sound pressure. A large value of kr means that either the frequency is high or the radius of curvature of the wave front is large. However, for values of k ² r ² small compared with 1, which means that the radius of curvature is small or the frequency is low, or both, the particle velocity is proportional to

| \tilde{p} | / (ω r)

$| \tilde{p} | / (ω r)$

. As a result, when a person talking or singing moves near to a pressure-gradient microphone so that r is small, his voice seems to have become more “boomy” or “bassy” because the output of the microphone increases with decreasing frequency.

Figure 5.6 (a) Directivity characteristic of the pressure-gradient microphone of Fig. 5.4. (b) Same but with scale in dB.

The path difference Δl depends on whether the diaphragm is a rigid piston or flexible. Because a microphone may be considered to be a sound source in reverse, we can use the radiation impedance of the equivalent rigid or flexible sound source to give us the relationship between the diaphragm pressure and velocity in Eqs. (5.1) and (5.11), which are rearranged as

Z_{s} = \frac{{\tilde{f}}_{D}}{S \tilde{u}} = j ω ρ_{0} Δ l \cos θ,

$Z_{s} = \frac{{\tilde{f}}_{D}}{S \tilde{u}} = j ω ρ_{0} Δ l \cos θ,$

(5.12)

so that we can solve for Δl. We will assume that the incident sound waves are on-axis so that θ = 0. In the case of a rigid circular piston of radius a with no baffle, the specific radiation impedance Z _s is given by

{Z_{s} |}_{λ > > a} = \frac{{\tilde{f}}_{D}}{S \tilde{u}} = j ρ_{0} c \frac{4 k a}{3 π} .

${Z_{s} |}_{λ > > a} = \frac{{\tilde{f}}_{D}}{S \tilde{u}} = j ρ_{0} c \frac{4 k a}{3 π} .$

(5.13)

Equating Eqs. (5.12) and (5.13) yields

Δ l = \frac{4 a}{3 π} .

$Δ l = \frac{4 a}{3 π} .$

(5.14)

Using the resilient disk in free space model to give the radiation impedance for a perfectly flexible diaphragm, where

{Z_{s} |}_{λ > > a} = j ρ_{0} c π k a / 4,

${Z_{s} |}_{λ > > a} = j ρ_{0} c π k a / 4,$

we find that

Δ l = \frac{π a}{4} .

$Δ l = \frac{π a}{4} .$

(5.15)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Acoustics

Create new playlist

Sign In

Sign Up

5.2. Pressure-gradient microphones

Table of Contents for
Acoustics