Acoustics

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

13.17. Radiation from a rigid rectangular piston in an infinite baffle [39,40]

Far-field pressure

Using the product theorem given in Section 13.16, the directivity pattern is equal to the product of the directivity patterns for two line arrays at right angles to each other [see Eq. (4.89)]. The directivity pattern for this type of radiating source with dimensions l _x and l _y is given by the formula

D (θ_{x}, θ_{y}) = \frac{\sin (\frac{1}{2} k l_{x} \sin θ_{x})}{\frac{1}{2} k l_{x} \sin θ_{x}} \cdot \frac{\sin (\frac{1}{2} k l_{y} \sin θ_{y})}{\frac{1}{2} k l_{y} \sin θ_{y}},

$D (θ_{x}, θ_{y}) = \frac{\sin (\frac{1}{2} k l_{x} \sin θ_{x})}{\frac{1}{2} k l_{x} \sin θ_{x}} \cdot \frac{\sin (\frac{1}{2} k l_{y} \sin θ_{y})}{\frac{1}{2} k l_{y} \sin θ_{y}},$

(13.318)

where θ _x is the angle between the normal to the surface of the piston and the projection of the line joining the middle of the surface and the observation point on the plane normal to the surface and parallel to l _x; θ _y is the same as θ _x, with l _y substituted for l _x.

It is often more convenient to express Eq. (13.318) using spherical coordinates using

\sin θ_{x} = \sin θ \cos ϕ, \sin θ_{y} = \sin θ \sin ϕ .

$\sin θ_{x} = \sin θ \cos ϕ, \sin θ_{y} = \sin θ \sin ϕ .$

(13.319)

Also, we shall substitute sinc x = (sin x)/x to obtain

D (θ, ϕ) = sinc (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot sinc (\frac{1}{2} k l_{y} \sin θ \sin ϕ) .

$D (θ, ϕ) = sinc (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot sinc (\frac{1}{2} k l_{y} \sin θ \sin ϕ) .$

(13.320)

Radiation impedance

Using the Bouwkamp impedance theorem, the radiation resistance and reactance can be found by inserting Eq. (13.320) into Eqs. (13.271) and (13.272) respectively to give

R_{s} = k l_{x} k l_{y} \frac{ρ_{0} c}{π^{2}} \int_{0}^{\frac{π}{2}} \int_{0}^{\frac{π}{2}} {sinc}^{2} (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot {sinc}^{2} (\frac{1}{2} k l_{y} \sin θ \sin ϕ) \sin θ d θ d ϕ,

$R_{s} = k l_{x} k l_{y} \frac{ρ_{0} c}{π^{2}} \int_{0}^{\frac{π}{2}} \int_{0}^{\frac{π}{2}} {sinc}^{2} (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot {sinc}^{2} (\frac{1}{2} k l_{y} \sin θ \sin ϕ) \sin θ d θ d ϕ,$

(13.321)

X_{s} = - j k l_{x} k l_{y} \frac{ρ_{0} c}{π^{2}} \int_{0}^{\frac{π}{2}} \int_{\frac{π}{2} + j 0}^{\frac{π}{2} + j \infty} {sinc}^{2} (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot {sinc}^{2} (\frac{1}{2} k l_{y} \sin θ \sin ϕ) \sin θ d θ d ϕ,

$X_{s} = - j k l_{x} k l_{y} \frac{ρ_{0} c}{π^{2}} \int_{0}^{\frac{π}{2}} \int_{\frac{π}{2} + j 0}^{\frac{π}{2} + j \infty} {sinc}^{2} (\frac{1}{2} k l_{x} \sin θ \cos ϕ) \cdot {sinc}^{2} (\frac{1}{2} k l_{y} \sin θ \sin ϕ) \sin θ d θ d ϕ,$

(13.322)

where R _s is the specific radiation resistance in N·s/m³ (rayl). The bold R indicates that the quantity varies with frequency, and X _s is the specific radiation reactance in N·s/m³ (rayl). Substituting t = sin θ in Eqs. (13.321) and (13.322) yields

R_{s} = \frac{k l_{x} l_{y} ρ_{0} c}{4 π^{2}} \int_{0}^{π / 2} \int_{0}^{1} {sinc}^{2} (\frac{k l_{x}}{2} t \cos ϕ) {sinc}^{2} (\frac{k l_{y}}{2} t \sin ϕ) \frac{t d t d ϕ}{\sqrt{1 - t^{2}}},

$R_{s} = \frac{k l_{x} l_{y} ρ_{0} c}{4 π^{2}} \int_{0}^{π / 2} \int_{0}^{1} {sinc}^{2} (\frac{k l_{x}}{2} t \cos ϕ) {sinc}^{2} (\frac{k l_{y}}{2} t \sin ϕ) \frac{t d t d ϕ}{\sqrt{1 - t^{2}}},$

(13.323)

X_{s} = \frac{k l_{x} l_{y} ρ_{0} c}{4 π^{2}} \int_{0}^{π / 2} \int_{1}^{\infty} {sinc}^{2} (\frac{k l_{x}}{2} t \cos ϕ) {sinc}^{2} (\frac{k l_{y}}{2} t \sin ϕ) \frac{t d t d ϕ}{\sqrt{t^{2} - 1}},

$X_{s} = \frac{k l_{x} l_{y} ρ_{0} c}{4 π^{2}} \int_{0}^{π / 2} \int_{1}^{\infty} {sinc}^{2} (\frac{k l_{x}}{2} t \cos ϕ) {sinc}^{2} (\frac{k l_{y}}{2} t \sin ϕ) \frac{t d t d ϕ}{\sqrt{t^{2} - 1}},$

(13.324)

where we note that sin(π/2 + j∞) = cos j∞ = cosh ∞ = ∞. An analytical solution to Eq. (13.323) can be found by substituting s = sin ϕ and expanding the sinc functions using

{sinc}^{2} x = {(\sin x)}^{2} / x^{2} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1} 2^{2 n - 1}}{(2 n)!} x^{2 n - 2},

${sinc}^{2} x = {(\sin x)}^{2} / x^{2} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1} 2^{2 n - 1}}{(2 n)!} x^{2 n - 2},$

(13.325)

which gives

R_{s} = \frac{ρ_{0} c}{\sqrt{π}} \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \frac{{(- 1)}^{m + n}}{(2 m + 1) (2 n + 1) (m + 1)! (n + 1)! Γ (m + n + \frac{3}{2})} {(\frac{k l_{x}}{2})}^{2 m + 1} {(\frac{k l_{y}}{2})}^{2 n + 1} .

$R_{s} = \frac{ρ_{0} c}{\sqrt{π}} \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \frac{{(- 1)}^{m + n}}{(2 m + 1) (2 n + 1) (m + 1)! (n + 1)! Γ (m + n + \frac{3}{2})} {(\frac{k l_{x}}{2})}^{2 m + 1} {(\frac{k l_{y}}{2})}^{2 n + 1} .$

(13.326)

A somewhat more complicated evaluation of the integrals in Eq. (13.324) is given in Ref. [40]. Firstly, the sine squared terms have to be expanded into cosine terms using Eqs. (A2.46) and (A2.50) from Appendix II. Then the infinite integral is evaluated before expanding the resulting Bessel and Struve functions. The range of the remaining finite integral has to be split into two at

l_{x} / \sqrt{l_{x}^{2} + l_{y}^{2}}

$l_{x} / \sqrt{l_{x}^{2} + l_{y}^{2}}$

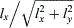yielding

X_{s} = \frac{2 ρ c}{π} (\frac{1 - sinc (k l_{x})}{q k l_{x}} + \frac{1 - sinc (q k l_{x})}{k l_{x}} + \sum_{m = 0}^{M} \frac{{(- 1)}^{m} f_{m} (q)}{(2 m + 1) m! (m + 1)!} {(\frac{k l_{x}}{2})}^{2 m + 1}),

$X_{s} = \frac{2 ρ c}{π} (\frac{1 - sinc (k l_{x})}{q k l_{x}} + \frac{1 - sinc (q k l_{x})}{k l_{x}} + \sum_{m = 0}^{M} \frac{{(- 1)}^{m} f_{m} (q)}{(2 m + 1) m! (m + 1)!} {(\frac{k l_{x}}{2})}^{2 m + 1}),$

(13.327)

where q = l _y/l _x,

f_{m} (q) = \frac{{}_{2}F_{1} (1, m + \frac{1}{2}; m + \frac{3}{2}, \frac{1}{1 + q^{2}}) + {}_{2}F_{1} (1, m + \frac{1}{2}; m + \frac{3}{2}, \frac{1}{1 + q^{- 2}})}{(2 m + 1) {(1 + q^{- 2})}^{m + 1 / 2}} + \frac{1}{2 m + 3} \sum_{n = 0}^{m} g_{m n} (q),

$f_{m} (q) = \frac{{}_{2}F_{1} (1, m + \frac{1}{2}; m + \frac{3}{2}, \frac{1}{1 + q^{2}}) + {}_{2}F_{1} (1, m + \frac{1}{2}; m + \frac{3}{2}, \frac{1}{1 + q^{- 2}})}{(2 m + 1) {(1 + q^{- 2})}^{m + 1 / 2}} + \frac{1}{2 m + 3} \sum_{n = 0}^{m} g_{m n} (q),$

(13.328)

and

\begin{matrix} g_{m n} (q) = (\begin{matrix} 2 m + 3 \\ 2 n \end{matrix}) \sum_{p = n}^{m} \frac{{(- 1)}^{p - n} q^{2 n - 1}}{(2 p - 1) {(1 + q^{2})}^{p - 1 / 2}} (\begin{matrix} m - n \\ p - n \end{matrix}) \\ + (\begin{matrix} 2 m + 3 \\ 2 n + 3 \end{matrix}) \sum_{p = m - n}^{m} \frac{{(- 1)}^{p - m + n} q^{2 n + 2}}{(2 p - 1) {(1 + q^{- 2})}^{p - 1 / 2}} (\begin{matrix} n \\ p - m + n \end{matrix}) . \end{matrix}

$\begin{matrix} g_{m n} (q) = (\begin{matrix} 2 m + 3 \\ 2 n \end{matrix}) \sum_{p = n}^{m} \frac{{(- 1)}^{p - n} q^{2 n - 1}}{(2 p - 1) {(1 + q^{2})}^{p - 1 / 2}} (\begin{matrix} m - n \\ p - n \end{matrix}) \\ + (\begin{matrix} 2 m + 3 \\ 2 n + 3 \end{matrix}) \sum_{p = m - n}^{m} \frac{{(- 1)}^{p - m + n} q^{2 n + 2}}{(2 p - 1) {(1 + q^{- 2})}^{p - 1 / 2}} (\begin{matrix} n \\ p - m + n \end{matrix}) . \end{matrix}$

(13.329)

Separate plots of R _s/ρ ₀ c and X _s/ρ ₀ c are shown in Figs. 13.43 and 13.44 respectively as a function of kl, where l = l _x is the smallest dimension. Separate plots of R _s/ρ ₀ c and X _s/ρ ₀ c are also shown in Figs. 13.45 and 13.46 respectively as a function of ka, where a is a notional radius that gives the same circular area S as the actual area of the rectangular piston, which is given by S = πa ² = l _x l _y.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Acoustics

Create new playlist

Sign In

Sign Up

13.17. Radiation from a rigid rectangular piston in an infinite baffle [39,40]

Far-field pressure

Radiation impedance

Table of Contents for
Acoustics