13.12. The Babinet–Bouwkamp principle
Kirchhoff theory
In its original form, Babinet's principle [34] simply states that the diffraction pattern resulting from the transmission of a plane wave through an aperture in an infinite screen is equivalent to that produced by the scattering of the same incident wave by the complementary disk. In the Kirchhoff theory of diffraction [35], it is assumed that the screen and complementary disk are either both rigid or both resilient, in which case the field scattered by an aperture in a rigid screen or complementary rigid disk can be represented by radiation from a rigid piston in an infinite baffle. Similarly, the field scattered by an aperture in a resilient screen or complementary resilient disk can be represented by radiation from a resilient disk in free space. If this were true, it would make life much simpler as everything could be calculated from closed-form solutions. The problem is that the former assumes that the velocity of the scattered wave at the aperture or complementary rigid disk is the same as that of the incident wave, as if it were unaffected by the presence of the scattering object. Similarly, the latter assumes that the pressure of the scattered wave at the aperture or complementary resilient disk is the same as that of the incident wave. At best, this is an approximation [22] that can only be used when the wavelength is much smaller than the aperture or disk.
Bouwkamp theory
Bouwkamp's modified version [20] of Babinet's principle states that the diffraction pattern resulting from the transmission of a plane wave through an aperture in an infinite rigid screen (see Fig. 13.37c) is equivalent to that produced by the scattering of the same incident wave by the complementary resilient disk (see Fig. 13.37f). Also, the flip side of this is that the diffraction pattern resulting from the transmission of a plane wave through an aperture in an infinite resilient screen (see Fig. 13.38c) is equivalent to that produced by the scattering of the same incident wave by the complementary rigid disk (see Fig. 13.38f). Furthermore, Bouwkamp states that:
- • The sound field scattered by a rigid disk is equivalent to that produced if the disk itself were radiating in free space, provided that the velocity at the surface of the disk is equal to that of the incident plane wave in the absence of any scattering obstacle.
- • The sound field scattered by a resilient disk is equivalent to that produced if the disk itself were radiating in an infinite rigid baffle, provided that the pressure at the surface of the disk is equal to that of the incident plane wave in the absence of any scattering obstacle.
Reflection from plane rigid objects [31]
We have already discussed the radiation of sound from moving surfaces using the boundary integral method. It often happens in acoustics that once you have found a solution for one problem, you get another for free. This is certainly the case with reflection from plane objects, and here it will be shown how. Imagine a plane wave being
reflected from an arbitrary rigid surface. At the surface, the normal velocity is zero. Now we let the resulting pressure field
 comprise two components as follows:
comprise two components as follows:

where
 is the incident wave in the absence of any obstacles and
is the incident wave in the absence of any obstacles and
 is the scattered wave. To satisfy the boundary condition of zero normal velocity at the surface, the normal velocity of the surface producing the scattered wave must be equal and opposite to the component of the velocity of the incident wave that is normal to the surface. This is easiest to illustrate with a planar obstacle such as a circular disk in free space, as shown in Fig. 13.8 except that in this case it is perfectly rigid. Let
is the scattered wave. To satisfy the boundary condition of zero normal velocity at the surface, the normal velocity of the surface producing the scattered wave must be equal and opposite to the component of the velocity of the incident wave that is normal to the surface. This is easiest to illustrate with a planar obstacle such as a circular disk in free space, as shown in Fig. 13.8 except that in this case it is perfectly rigid. Let
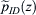 be a simple plane incident wave traveling along the disk's axis of symmetry, which in this case is defined as the z-axis, and let the disk be located at z
=
0. At the disk, the velocity and hence also the gradient of the resultant field
be a simple plane incident wave traveling along the disk's axis of symmetry, which in this case is defined as the z-axis, and let the disk be located at z
=
0. At the disk, the velocity and hence also the gradient of the resultant field
 are both zero:
are both zero:
where w is the radial ordinate and a is the radius of the disk. Also, from Eq. (13.257) and to preserve continuity, the resultant pressure gradient is the sum of the incident and scattered pressure gradients:
Hence, the velocity
 of the disk is equal and opposite to the velocity
of the disk is equal and opposite to the velocity
 of the incident wave in the absence of any scattering obstacles:
of the incident wave in the absence of any scattering obstacles:
Therefore, the scattered field
 is that which would be produced if the disk were oscillating back and forth with the same velocity as the incident wave, but with opposite phase, and the resultant field
is that which would be produced if the disk were oscillating back and forth with the same velocity as the incident wave, but with opposite phase, and the resultant field
 is the sum of the incident and scattered fields:
is the sum of the incident and scattered fields:
as expressed in Fig. 13.38d–f. However, we have to ask whether scattered field
 is the same as that of a disk in free space or one in an infinite baffle. To answer that, we have to consider another boundary condition, which lies in the plane of the disk beyond its perimeter. We can already assume that the field on one side of this plane will be the symmetrical negative of that on the other. This can be explained by the fact that on the “bright” side (facing the incident wave), the radiated sound represents the reflected sound, whereas on the “dark” side, it is of opposite phase and therefore cancels the incident wave that would otherwise be present in the absence of the disk. However, in a baffle, these equal and opposite pressure values on either side of the baffle would produce a discontinuous field when added to the original incident wave. Therefore, the disk must behave as though it is oscillating in free space, thus producing a continuous field with zero pressure in the plane beyond its perimeter as shown in Fig. 13.38f. Hence, the resultant pressure in that region is simply that of the incident wave in the absence of any obstacles. The scattered field
is the same as that of a disk in free space or one in an infinite baffle. To answer that, we have to consider another boundary condition, which lies in the plane of the disk beyond its perimeter. We can already assume that the field on one side of this plane will be the symmetrical negative of that on the other. This can be explained by the fact that on the “bright” side (facing the incident wave), the radiated sound represents the reflected sound, whereas on the “dark” side, it is of opposite phase and therefore cancels the incident wave that would otherwise be present in the absence of the disk. However, in a baffle, these equal and opposite pressure values on either side of the baffle would produce a discontinuous field when added to the original incident wave. Therefore, the disk must behave as though it is oscillating in free space, thus producing a continuous field with zero pressure in the plane beyond its perimeter as shown in Fig. 13.38f. Hence, the resultant pressure in that region is simply that of the incident wave in the absence of any obstacles. The scattered field
 is that of a rigid disk oscillating in free space, which has already been evaluated in Section 13.10, using the dipole part of the Kirchhoff–Helmholtz boundary integral.
is that of a rigid disk oscillating in free space, which has already been evaluated in Section 13.10, using the dipole part of the Kirchhoff–Helmholtz boundary integral.
Reflection from plane resilient objects
In the case of a resilient disk in the presence of an incident plane wave traveling toward it along its axis of symmetry, the boundary condition at its surface is that of zero pressure:
Hence, the pressure of the scattered field at the surface must be equal and opposite to the pressure of the incident wave in the absence of any scattering obstacles:
Therefore, the scattered field
 is that which would be produced if the disk were in motion with the same pressure as the incident wave, but opposite phase, and the resultant field
is that which would be produced if the disk were in motion with the same pressure as the incident wave, but opposite phase, and the resultant field
 is the sum of the incident and scattered fields:
is the sum of the incident and scattered fields:
as expressed in Fig. 13.37d–f. Furthermore, the scattered fields on each side of the disk are symmetrical and both of opposite polarity to the incident wave. This has the effect of creating a shadow on the “dark” side and reversing the phase of the reflected wave on the “bright” side because of the boundary condition of zero pressure, as opposed to zero velocity. If the boundary condition in the plane beyond the perimeter of the disk were one of zero pressure, the velocities on each side would be equal and opposite thus adding to and subtracting from the velocity of the incident wave on consecutive sides. This would in turn lead to a discontinuity in the velocity distribution of the resultant field at the plane. Hence, the scattered field is that of a resilient disk in an infinite baffle with symmetrical fields on each side, or a “breathing” resilient disk, which we have already evaluated in Section 13.9, using the monopole part of the Kirchhoff–Helmholtz boundary integral.
The Babinet–Bouwkamp principle for diffraction through a circular aperture in a rigid screen
Essentially, the boundary conditions for a circular aperture in an infinite rigid screen are the same as those for the complementary rigid disk in free space above and Fig. 13.38d, except that they are interchanged as shown in Fig. 13.37a. Hence, the resultant velocity is zero at the screen, which is the scattering obstacle, and the pressure in the aperture is the same as that of the incident wave in the absence of any scattering obstacles. However, although the rigid disk itself was treated as the source of the scattered wave, it is not so convenient to treat the infinite rigid screen as such. Instead, the aperture is treated as the source whereby the pressure is uniform everywhere within it and the aperture acts as a pressure source, namely a resilient disk in an infinite baffle, which we have already evaluated in Section 13.9, using the monopole part of the Kirchhoff–Helmholtz boundary integral, and satisfies the boundary condition of zero velocity on the screen. To calculate the resultant field on both sides of the screen, we simply add the scattered field to the incident field in the absence of an aperture, i.e., the incident plane wave plus its reflection from a continuous infinite rigid screen plus the radiation from the resilient disk. This is illustrated in Fig. 13.37a–c. For clarity, the diagram portrays the scattering
of a sound wave at some very high frequency where there is minimal diffraction. However, the principle applies at all frequencies. In general, for diffraction through a circular aperture in a rigid screen,
 (13.265)
(13.265)
and
 (13.266)
(13.266)
The Babinet–Bouwkamp principle for diffraction through a circular aperture in a resilient screen
Here we interchange the boundary conditions for a resilient disk in free space, described above. Hence, the resultant pressure is zero at the screen, which is the scattering obstacle, and the velocity in the aperture is the same as that of the incident wave in the absence of any scattering obstacles. The aperture is treated as the source, namely a rigid disk in free space, which we have already evaluated in Section 13.10, using the dipole part of the Kirchhoff–Helmholtz boundary integral, and satisfies the boundary condition of zero pressure on the screen. To calculate the resultant field on both sides of the screen, we simply add the scattered field to the incident field in the absence of an aperture, i.e., the incident plane wave plus its reflection from a continuous infinite resilient screen plus the radiation from the rigid disk. This is illustrated in Fig. 13.38a–c. For clarity, the diagram portrays the scattering of a sound wave at some very high frequency where there is minimal diffraction. However, the principle applies at all frequencies. In general, for diffraction through a circular aperture in a resilient screen,
 (13.267)
(13.267)
and

 is the pressure magnitude,
is the pressure magnitude,
 is the incident pressure at the hole in the absence of a screen, ρ is the density of the acoustic medium, and c is the speed of sound in that medium.
is the incident pressure at the hole in the absence of a screen, ρ is the density of the acoustic medium, and c is the speed of sound in that medium.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.

