B.1 How to Prove Anything

OK, fine—we can't actually tell you how to prove everything. But we can give you some advice that will help you when you try to prove anything.

Writing a proof is more art than science. Although there may be a “correct” way to prove something (or several correct ways), there is still a wide range of styles, formats, and logical implications that follow the same basic argument. (Similarly, you and your friend might write very different essays on “How I Spent My Summer Vacation,” even if you did the same things during your vacations.)

Writing a proof is very much like arguing a case in court. (Or at least it's like how it looks on TV.) Like a courtroom argument, a proof should contain a beginning, a middle, and an end.

• The beginning tells us what is already known (the assumptions of the theorem), reminds us of important facts that are already in evidence that will be important for the proof, establishes new notation that you will use in the proof, and gives us a hint of where you're headed and what steps the proof will take. Here are some examples:

  Courtroom Claim: Dr. Evil is guilty of stealing pencils from Prof. Plum's desk.

  Courtroom Argument: Consider the man sitting before you, Dr. Evil. You already know that security camera video from the night of October 6 shows Dr. Evil entering Prof. Plum's office building. Let the security video tape from that night be labeled as “Exhibit A.” Today I will convince you, beyond a reasonable doubt, that Dr. Evil stole pencils from Prof. Plum's desk on that night. I will do this by providing physical evidence placing Dr. Evil in Prof. Plum's office and demonstrating that Dr. Evil had, indeed, touched pencils recently.

  See how similar their structures are?

• The middle provides the evidence that proves the claim. Like evidence in a trial, the steps in your proof must follow logically from one another and must be straightforward to follow.

  Courtroom Argument: Exhibit A shows Dr. Evil entering Prof. Plum's office building at 11:37 PM. At approximately 11:45 PM, graduate students saw a secretive figure attempting to pick the lock on Prof. Plum's office door. Dr. Evil's fingerprints were found on the door, and in Prof. Plum's office, on the following day (October 7), and since Prof. Plum's office had been steam‐cleaned the day before, the fingerprints must have been left on the night of October 6. Moreover, graphite stains on Dr. Evil's shirt match the precise composition of graphite contained in the pencils that Prof. Plum keeps in his desk.

  Note that, in the proof, we provided justification for the steps that were not immediately obvious but omitted justification for the easy algebraic step. What counts as “easy” or “obvious” is, of course, a subjective matter. In general, a good rule of thumb to use is that, if your fellow students were reading your proof, they should be able to follow each step without having to look up any facts or write down any additional derivations.

• The end is the arrival point—the claim you are trying to prove.

  Courtroom Argument: Ladies and gentlemen of the jury, the preponderance of evidence demonstrates that Dr. Evil has committed this heinous crime. You have no choice but to find him guilty.

Just like the lawyer's argument, the proof uses words—not just math—to lead the reader on the path from assumptions to conclusions. Of course, in a legal trial, facts and implications are subject to interpretation—that's why we have judges and juries. In a mathematical proof, however, all facts and logical implications should be incontrovertible.

B.2 Types of Things You May Be Asked to Prove

Here is a (very nonexhaustive) list of the kinds of statements you may be asked to prove in this book or at some other point in your proof‐writing career:

• 

  This is the simplest kind of statement (though that does not mean it will require the simplest proof). It simply asks you to prove that two mathematical objects are equal.

  Notice that in this example, there is a qualifying statement to set up the statement you are asked to prove; this is fairly typical.

• 

  The symbols p and q stand here not for variables but for statements. The symbol is interpreted as “p implies q,” and it is the same as saying “if p then q.”

  Here p is “ ” and q is equation B.2).

• 

  The symbol means “if and only if” (sometimes abbreviated “iff”). The claim indicates that either both statements are true or both are false. Another description for this kind of statement is that q is a necessary and sufficient condition for p—in order for p to be true, q must be true, and the truth of q is sufficient to ensure the truth of p.

  To prove an iff statement, you must prove both directions of the implication—that is, you must prove that p implies q and that q implies p. Sometimes you can do this all at once using a string of iff implications:

  

  In other cases, though, the proof needs to be divided into two parts. In the first part, you prove one implication (e.g., ), and in the second part, you prove the reverse implication ( , or its logical equivalent, ).

• such that [condition], [statement].

  Here you are asked to prove that for all x that satisfy a certain [condition], some [statement] is true.

  To prove a “ ” claim, you take the [condition] as given and prove that the [statement] is true. This actually feels a lot like a “ ” claim, and in fact they are often logically equivalent.

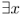• such that [statement].

  This time you need to prove that there exists (at least one) x that satisfies the [statement]. Sometimes there are qualifying conditions on the type of x that are allowed.

  (In this case, there are many x that will do the trick, but you are asked only to prove the existence of one of them.)

• 

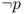
  In other words, you are being asked to disprove the statement p.

  In general, it suffices to find a single example for which p is not true. In the example above, you just need to find two convex functions whose product is not convex.

  However, if p is of the form “ such that [statement],” then to disprove p you must prove that the [statement] is false for all x. This may be easy or hard. Here's a hard example:

  (This is Fermat's Last Theorem, which went unproved for over 350 years until it was finally proved in 1995.)

B.3 Proof Techniques

This section will give you a quick overview of several types of proofs—strategies for proving theorems. (Of course, there are others that this list does not include.) These are tools in your proof‐building toolbox. It's your job to figure out which tool(s) to use for each job.

B.4 Other Advice

• Provide explanations, not just math. Even though your reader may be a smart mathematician, you should still provide verbal explanations that explain the intuition behind the math whenever the math is a bit complicated. This applies to derivations, but also to definitions.

  For example, suppose you want to say:

  Let be the order times, let T be the set of order times, let , and let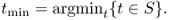

  Then you may wish to help out your reader a bit by also saying:

  That is, S is the set of order times for which the inventory level (just before ordering) is positive, and 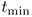is the earliest such time.

• Distinguish between definitional and derivational 's. The sign has two meanings: One means “let the left‐hand side be defined to equal the right‐hand side” and the other means “I have now proved that the left‐hand side equals the right‐hand side.” The first is a definitional equality, the second is a derivational equality. It is important to differentiate between them. The best way to do this is using words: “Let 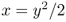.” “Therefore, .” (The difference between these two types of equality is exactly the same as the difference between = and == in C/C++, Java, and other programming languages. It's also the difference between and in the pseudocode in this book.)

  For example, consider the following proof fragment:

  

  This fragment is confusing. Is v a new symbol that is being defined as ? Or do we already know that ? Did the first step prove that ? Or do we already know that ? Or is it another new symbol?

  True, a smart reader might be able to figure all this out. But the reader's life would be a lot easer if the proof‐writer instead wrote:

  We know that . Let . Since (by Theorem 4.3), we have

  

  This bullet is really a special case of the next.

• Use complete sentences. The first proof fragment in the previous bullet (starting with ) becomes a lot easier to read when it's written using complete sentences. If you use sentences, the ambiguities of the sign are resolved. The same could be said about many other mathematical ambiguities and confusions. Writing in complete sentences—even if your English isn't very good—will instantly make your proofs easier to read.
• Typeset thoughtfully. If you are writing your proofs by hand, take care to write them neatly, and think carefully about how the proof will be laid out, including your use of white space. Even better, type your proofs using LATE X or another software package for typesetting mathematical text. Invest the time to learn how to typeset complicated math so that it looks nice and helps convey your meaning. Be considerate of your reader.

  For example, consider the following proof fragment:

  

  The math would be a lot easier to follow if the proof‐writer had written the fractions the way they were intended to be written:

  

  In general, thoughtfully typeset math will make your proof easier to read.

• Don't stop here. There are many books and other resources for learning how to write proofs. (See, e.g., Sundstrom (2006) and Velleman (2006).) There are also lots of web sites devoted to the topic. Like web sites devoted to any topic, some of these are very good and others are very bad, so be a good critic when you read.