Appendix A
Multiple‐Chapter Problems
PROBLEMS
- A.1 (Worst‐Case Bound for Deterministic Newsvendor Approximation) As noted in Section 5.3.2, the papers by Zheng (1992) and Axsäter (1996) suggest bounds on the error that results from approximating a stochastic inventory model (the model of Section 5.1, for which an
 policy is optimal) by a deterministic one. Suppose we do the same thing for the newsvendor model, setting S equal to the optimal solution to the deterministic problem, i.e.,
policy is optimal) by a deterministic one. Suppose we do the same thing for the newsvendor model, setting S equal to the optimal solution to the deterministic problem, i.e.,  . Assume the demand is distributed
. Assume the demand is distributed  .
.- Prove that

where
 is the expected newsvendor cost if S is the order‐up‐to level and
is the expected newsvendor cost if S is the order‐up‐to level and  .
. - Is it possible to identify a fixed worst‐case bound
 that holds for any values of the parameters
that holds for any values of the parameters  , and
, and  ? Explain your answer.
? Explain your answer.
- Prove that
- A.2 (Optimizing Compost Inventory) The compost facilities in Greentown move finished compost (organic matter that has completed the composting process) from the processing area to a large pile in the pick‐up area for residents of the town to pick up for use in their gardens, free of charge.
- At the compost facility in the Appleville neighborhood of Greentown, residents pick up compost at a steady rate of 700 cubic yards per week. The facility has committed to keeping the pick‐up area stocked, i.e., never having residents arrive to find no compost there.
Finished compost is moved from the processing area to the pick‐up area by truck, and each time the facility wishes to do this, it must hire a truck driver for a day. This costs $320, and once the driver is hired, the facility can move as much finished compost as it wishes. You can assume it takes negligible time to move the compost. Finished compost that remains in the pick‐up area must be tended by the staff (e.g., cleaning up spills), at a cost of $0.05 per cubic yard per day.
Using the EOQ model, calculate the optimal order quantity,
 , and the optimal average cost per week,
, and the optimal average cost per week,  .
. - At the compost facility in the Beantown neighborhood of Greentown, the daily demand for compost is stochastic (unlike at the Appleville facility), with probabilities given in Table A.1. At this facility, the staff moves finished compost from the processing site to the pick‐up site every morning, before the facility opens to customers. The truck drivers are staff members and so no additional labor charge is incurred for these activities.
If the pick‐up area runs out of compost, for the remainder of the day the staff must deliver compost directly to customers' vehicles, at a cost of $0.25 per cubic yard. The staff do not tend to the pick‐up area during the day (as they do at the Appleville facility), but if there is any finished compost in the pick‐up area when the facility closes at the end of the day, they must move it back to the processing area, at a cost of $0.10 per cubic yard.
What is the optimal number of cubic yards of finished compost to move to the pick‐up area each morning?
Table A.1 Demand for finished compost for Problem A.2(b).
Cumulative d Probability 
Probability 
0 0.12 0.12 1 0.05 0.17 2 0.07 0.24 3 0.11 0.35 4 0.24 0.59 5 0.17 0.76 6 0.11 0.87 7 0.07 0.94 8 0.04 0.98 9 0.02 1.00
- At the compost facility in the Appleville neighborhood of Greentown, residents pick up compost at a steady rate of 700 cubic yards per week. The facility has committed to keeping the pick‐up area stocked, i.e., never having residents arrive to find no compost there.
- A.3 (Inventory Optimization for Deterministic Bass Demands) A new model of wireless router will be introduced shortly. An electronics retail chain expects the aggregate demand for the router at its stores to follow a discrete‐time Bass diffusion process (2.50) with parameters
 ,
,  , and
, and  . Each time period represents one week. The retail chain holds inventory of the routers at its central warehouse and has an opportunity to place a replenishment order once per week. Each order incurs a fixed cost of $800, and each router held in inventory incurs a holding cost of $0.04 per week. The planning horizon is 52 weeks; any demand after the horizon ends can be ignored. In which weeks should the retailer place orders for routers, and what are the optimal order quantities? What is the total cost?
. Each time period represents one week. The retail chain holds inventory of the routers at its central warehouse and has an opportunity to place a replenishment order once per week. Each order incurs a fixed cost of $800, and each router held in inventory incurs a holding cost of $0.04 per week. The planning horizon is 52 weeks; any demand after the horizon ends can be ignored. In which weeks should the retailer place orders for routers, and what are the optimal order quantities? What is the total cost? - A.4 (Inventory Optimization for Stochastic Bass Demands) Suppose that the demand for wireless routers in Problem A.3 is now stochastic. The demand in period t is normally distributed with a mean of
 and a standard deviation of
and a standard deviation of  , where
, where  is given by the discrete‐time Bass model (2.50). Unmet demands are backordered, incurring a stockout cost of $1.25 per router per week. Assume
is given by the discrete‐time Bass model (2.50). Unmet demands are backordered, incurring a stockout cost of $1.25 per router per week. Assume 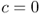 and
and  . The other cost parameters, and the Bass parameters, are as given in Problem A.3. Although we assumed in Section 4.5.2.2 that the demand process is stationary, an
. The other cost parameters, and the Bass parameters, are as given in Problem A.3. Although we assumed in Section 4.5.2.2 that the demand process is stationary, an  policy is still optimal for this problem with nonstationary demands. Determine the optimal parameters,
policy is still optimal for this problem with nonstationary demands. Determine the optimal parameters,  and
and  , for every period, and report the values for periods
, for every period, and report the values for periods  , and 52.
, and 52. - A.5 (Subscription‐Selling Newsvendor) Suppose that, rather than selling individual newspapers, the newsvendor sells subscriptions to the newspaper. The subscription is a little unusual and works as follows: There are N customers, and the newsvendor must decide which customers to select. Customers typically request multiple newspapers each day, and customer i's daily demand is
 . Demands are statistically independent from one customer to another. If customer i is selected, the newsvendor earns a subscription revenue of
. Demands are statistically independent from one customer to another. If customer i is selected, the newsvendor earns a subscription revenue of  per day. This revenue is independent of the actual demand.
per day. This revenue is independent of the actual demand. Just like in the classical newsvendor problem, our newsvendor must decide at the beginning of the day how many newspapers to stock. During the day, random demands are observed from each of the newsvendor's selected customers. At the end of the day, the newsvendor incurs a holding cost of h per unsold newspaper and a stockout cost of p per unmet demand.
Note that the newsvendor must choose his customers, and his order quantity, before demands are observed.
- Formulate a mathematical programming model to choose customers in order to maximize the expected profit (revenue minus costs) per day. If you introduce any additional notation, define it clearly.
Hint: Your model should not need a decision variable that represents the order quantity.
- Formulate a polynomial‐time algorithm that solves this problem exactly (i.e., not a heuristic). Describe your algorithm step‐by‐step and explain clearly why it produces the optimal solution every time.
- What is the complexity of your algorithm (e.g.,
 )?
)? - Suppose
 and
and  . The table below lists parameters for four customers. Using your algorithm, determine the optimal set of customers to serve. Report the optimal set of customers and the resulting expected profit.
. The table below lists parameters for four customers. Using your algorithm, determine the optimal set of customers to serve. Report the optimal set of customers and the resulting expected profit.
- Formulate a mathematical programming model to choose customers in order to maximize the expected profit (revenue minus costs) per day. If you introduce any additional notation, define it clearly.
- A.6 (EOQ with Market Selection) Consider a single production stage that manufactures a single item. (We can equivalently view this “production stage” as a retail ordering process that plans orders for a single item.) Let
 denote a set of potential markets, indexed by i. Producing the product results in a setup cost K and a variable cost c per item procured. Inventory costs are assessed at a rate of h dollars per unit per year. Market i has a constant and deterministic annual demand rate,
denote a set of potential markets, indexed by i. Producing the product results in a setup cost K and a variable cost c per item procured. Inventory costs are assessed at a rate of h dollars per unit per year. Market i has a constant and deterministic annual demand rate,  . We let
. We let  denote the per‐unit revenue from market i less any variable production and (possibly market‐specific) delivery costs. Unlike the standard EOQ model, the producer can choose whether or not to satisfy each market's demand. If the producer chooses to supply a certain market, then it must satisfy all of the demand for that market. Rather than minimizing the average annual cost, as in the EOQ model, we maximize the average annual net contribution to profit.
denote the per‐unit revenue from market i less any variable production and (possibly market‐specific) delivery costs. Unlike the standard EOQ model, the producer can choose whether or not to satisfy each market's demand. If the producer chooses to supply a certain market, then it must satisfy all of the demand for that market. Rather than minimizing the average annual cost, as in the EOQ model, we maximize the average annual net contribution to profit.- Write an expression for the average annual net contribution to profit and discuss how to solve the corresponding optimization problem. Define any new notation that you introduce.
- Suppose that we begin with an n‐market problem for which an optimal solution selects markets
 , where
, where  , and then consider the same problem with a single additional new market,
, and then consider the same problem with a single additional new market,  . Prove the following proposition:
. Prove the following proposition:
- A.7 (EOQ with Random Half Orders, Take 2) Solve Problem 3.25, reinterpreting it as a yield uncertainty problem and using the results of Section 9.3. (Hint: Problem 9.15 justifies the use of the yield uncertainty results even for discrete yield distributions.)
- A.8 (Finite‐Horizon Transshipments) Consider a finite‐horizon version of the (infinite‐horizon) transshipment problem discussed in Section 7.4. In the finite‐horizon version of the problem, the long‐run expectations we calculated in Section 7.4 are no longer applicable; instead, we can only calculate expectations for individual periods, given the retailers' inventory levels at the start of the period. Dynamic programming is an appropriate tool for solving this problem. Assume the periods are numbered
 .
. The sequence of events given in Section 7.4.2 applies to this finite‐horizon problem as well. Let
 be the starting inventory level for retailer i in step 1 of the sequence of events, and let
be the starting inventory level for retailer i in step 1 of the sequence of events, and let  be the order‐up‐to level for retailer i in step 2; that is,
be the order‐up‐to level for retailer i in step 2; that is,  . Let
. Let  be the vector of starting inventory levels and
be the vector of starting inventory levels and  be the vector of order‐up‐to levels.
be the vector of order‐up‐to levels.To keep things simple, assume that retailer 2's demand is deterministic and equal to
 in each period. Assume further that retailer 2 always chooses an order‐up‐to level
in each period. Assume further that retailer 2 always chooses an order‐up‐to level  that is at least equal to
that is at least equal to  , so that it never experiences stockouts. This also means that transshipments only ever go in one direction: from retailer 2 to retailer 1.
, so that it never experiences stockouts. This also means that transshipments only ever go in one direction: from retailer 2 to retailer 1.- Let
 be the expected holding and stockout costs for retailer i in a given period assuming that
be the expected holding and stockout costs for retailer i in a given period assuming that  is the vector of order‐up‐to levels chosen in step 2. Then an expression for
is the vector of order‐up‐to levels chosen in step 2. Then an expression for  is:
is: 
Write an expression for
 .
. - Let
 be the expected transshipment costs in a given period assuming that
be the expected transshipment costs in a given period assuming that  is the vector of order‐up‐to levels chosen in step 2. Write an expression for
is the vector of order‐up‐to levels chosen in step 2. Write an expression for  .
. - Let
 be the optimal expected cost in periods
be the optimal expected cost in periods  if retailer i begins period t with inventory level
if retailer i begins period t with inventory level  (and each retailer acts optimally thereafter). Write an expression for
(and each retailer acts optimally thereafter). Write an expression for  . Your expression should make use of the functions defined above, as well as
. Your expression should make use of the functions defined above, as well as  .
.
- Let
- A.9 (Using Discrete Choice to Forecast Demand) A minor‐league baseball stadium has sold 8000 tickets to tonight's baseball game. The stadium sells three kinds of souvenirs: hats, T‐shirts, and puffy hands. Each person who attends the game will buy exactly one souvenir. From historical data, the concession manager at the stadium has developed an estimate,
 , of the utility that each attendee n derives from each of the souvenirs, for
, of the utility that each attendee n derives from each of the souvenirs, for 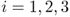 . These
. These  values are given Table A.3.
values are given Table A.3.- Assume that the actual utilities
 differ from the estimated utilities
differ from the estimated utilities  by an additive iid error term that has a standard Gumbel distribution. Using the multinomial logit model, calculate the expected demand for each souvenir.
by an additive iid error term that has a standard Gumbel distribution. Using the multinomial logit model, calculate the expected demand for each souvenir. - Let X be a random variable representing the total number of people who buy hats. What is the probability distribution of X? Specify the name and the parameters of the distribution.
- The concession manager replenishes the inventory of hats before the game, and any unsold hats after the game incur an opportunity cost of $0.25. Unmet demands for hats incur a stockout cost (including lost profit and loss of goodwill) of $1.75 per hat. How many hats should the manager stock for tonight's game?
Note: You may solve this problem using the discrete demand distribution you identified in part (b), or you may approximate this distribution with a continuous distribution. If you take the latter approach, justify your approximation carefully.
Table A.3
 values for Problem A.9.
values for Problem A.9.Souvenir 
Hat 0.48 T‐shirt 0.34 Puffy hand 0.21 - Assume that the actual utilities
- A.10 (Base‐Stock Policies with Disruptions) Consider a finite‐horizon, periodic‐review inventory system with stochastic demand and no fixed cost, for which we proved in Section 4.5.1.2 that a base‐stock policy is optimal. There are T periods, the lead time is 0, the demand per period is random with pdf
 and cdf
and cdf  , the holding cost is h per item per period, the backorder cost is p per item per period, the per‐unit ordering cost is c, and the discount factor is
, the holding cost is h per item per period, the backorder cost is p per item per period, the per‐unit ordering cost is c, and the discount factor is  . If the inventory level is x at the start of period T, we incur a terminal cost of
. If the inventory level is x at the start of period T, we incur a terminal cost of  , a convex function.
, a convex function. Now suppose that the supplier is unreliable, and that when an order is placed, the supplier delivers it with probability q (
 ). With probability
). With probability  , the supplier is disrupted—it's as though the order had never been placed, and the firm must wait until the next time period to order again. Evidently, the order placed in the next time period will be larger to make up for the failed order. (This is a special case of the model in Section 9.2.2 in which disruptions follow an iid Bernoulli process.)
, the supplier is disrupted—it's as though the order had never been placed, and the firm must wait until the next time period to order again. Evidently, the order placed in the next time period will be larger to make up for the failed order. (This is a special case of the model in Section 9.2.2 in which disruptions follow an iid Bernoulli process.)- Write an expression for
 , the expected cost in periods
, the expected cost in periods  if we begin period t with an inventory level equal to x and act optimally in every period. Your expression should be analogous to (4.85) and may use the function
if we begin period t with an inventory level equal to x and act optimally in every period. Your expression should be analogous to (4.85) and may use the function  . If you modify the definition of
. If you modify the definition of  , explain your modifications carefully.
, explain your modifications carefully. - Prove that a base‐stock policy is optimal in every period t.
Note: If you use any results from Section 4.5.1.2 to prove this, argue why these results are still true under your revised cost functions.
- Suppose
 . We know from Section 4.5.1.2 that the same S is optimal in every period if
. We know from Section 4.5.1.2 that the same S is optimal in every period if  . Do you think the same statement is true if
. Do you think the same statement is true if  ? Explain your answer.
? Explain your answer.
- Write an expression for
- A.11 (Coordinating the Unreliable Supply Chain) Consider the newsvendor problem with disruptions discussed in Section 9.2.2. In this problem, you will extend this model to consider the unreliable supplier and the coordination between the two players.
The supplier holds no inventory and has a lead time of 0 when operational. But the supplier is subject to disruptions, and when a disruption occurs, the supplier cannot provide any items. The retailer acts like a newsvendor with deterministic demand of d per period. Excess inventory at the end of the period is held over until the next period at a cost of
 per unit per period, and unmet demands are backordered, incurring a stockout penalty of
per unit per period, and unmet demands are backordered, incurring a stockout penalty of  per unit per period for the retailer and
per unit per period for the retailer and  for the supplier. Let
for the supplier. Let  .
.The supplier's disruption probability is
 and its recovery probability is
and its recovery probability is  . The steady‐state probability of being in a disruption that has lasted for n periods is
. The steady‐state probability of being in a disruption that has lasted for n periods is 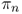 , and the cumulative probability of being in a disruption lasting n periods or fewer is
, and the cumulative probability of being in a disruption lasting n periods or fewer is  , as in (9.10).
, as in (9.10).Suppose the supplier and retailer have agreed upon a contract that specifies a transfer payment to be made from the retailer to the supplier in an amount based on the current state of the system. From (9.14), the retailer's expected cost can be expressed as a function of its base‐stock level S as follows:
(A.1)
where T is the expected transfer payment. Similarly, the supplier's expected cost is given by
(A.2)
and the total supply chain expected cost is given by
(A.3)
Let
 ,
,  , and
, and  be the retailer's, supplier's, and supply chain optimal base‐stock level, respectively.
be the retailer's, supplier's, and supply chain optimal base‐stock level, respectively.Note that this model is expressed in terms of costs, not profits, and that it assumes backorders, not lost sales; both are changes from the assumptions in Chapter 14.
- Suppose
 . Prove that
. Prove that  , and that for some instances, the inequality is strict (in which case the supply chain is not coordinated).
, and that for some instances, the inequality is strict (in which case the supply chain is not coordinated). - In one or two sentences, explain why the retailer tends to under‐order in part (a).
- Now consider a buyback contract in which the retailer pays the supplier w per unit ordered and the supplier pays the retailer b per unit on‐hand at the end of each period. (Note that the items remain on‐hand; they are not sent back to the supplier or destroyed. They can, rather, be used to satisfy demand in future periods.) Write expressions for
 ,
,  , and
, and  under this contract.
under this contract. - Write the optimal base‐stock levels
 ,
,  , and
, and  under this contract.
under this contract. - Find a value for b in terms of the other problem parameters such that
 .
. - Show that, using the b you found in the previous part,
 . Thus, the supply chain is coordinated.
. Thus, the supply chain is coordinated. - You should have found that b and the optimal S values don't depend on w. Explain in one or two sentences why this makes sense.
- Suppose
- A.12 (An Approximate Location–Routing Problem) Consider a facility location problem in which the customers assigned to each facility are served via a single truck whose route is determined by solving a traveling salesman problem (TSP). The length of the optimal TSP tour through n points located in an area A is often approximated as
 , where k is a constant. This approximation is called the “square‐root rule.” (See Section 10.6.5.)
, where k is a constant. This approximation is called the “square‐root rule.” (See Section 10.6.5.)- Formulate the problem of locating facilities to minimize the sum of the fixed cost and transportation cost, which is approximated using the square‐root rule. Make the (unrealistic) assumption that we know, in advance, that if facility j is opened, then the area of the region it will serve is equal to
 , where
, where  is a parameter of the model.
is a parameter of the model. - Propose an algorithmic method to solve this problem.
- Formulate the problem of locating facilities to minimize the sum of the fixed cost and transportation cost, which is approximated using the square‐root rule. Make the (unrealistic) assumption that we know, in advance, that if facility j is opened, then the area of the region it will serve is equal to
- A.13 (A Location–Flexibility Design Problem) We wish to locate facilities and decide which facilities will produce which products. Let P be the set of products. Customer demands are stochastic and are described by scenarios; let S be the set of scenarios and let
 be the probability that scenario
be the probability that scenario  occurs. There is a fixed cost
occurs. There is a fixed cost  if facility j is configured to produce product
if facility j is configured to produce product  . Facility
. Facility  has a fixed capacity of
has a fixed capacity of  , and it takes one unit of capacity to produce one unit of product p, for all
, and it takes one unit of capacity to produce one unit of product p, for all  . Transportation costs are product‐specific. We choose facility locations and capabilities (i.e., assignments of products to facilities) before the scenario is observed, and we set the production quantities, shipment quantities, and assignments of customers to facilities after the scenario is observed.
. Transportation costs are product‐specific. We choose facility locations and capabilities (i.e., assignments of products to facilities) before the scenario is observed, and we set the production quantities, shipment quantities, and assignments of customers to facilities after the scenario is observed.- Formulate a linear mixed‐integer programming model to minimize the expected cost of this system. Define any new notation clearly. Explain the objective function and each of the constraints in words.
- Sketch an idea for an algorithm to solve this problem.
- A.14 (Flying across the United States) Suppose you would like to fly to each of the 48 continental United States in your private airplane. You don't care where you go in each state; your only requirement is that you land your airplane in one airport per state and then return to the starting airport. Your goal is to minimize the total distance you fly. (The distance does not include the flight from your home airport to the starting airport on your route.)
This problem is an example of the generalized traveling salesman problem (GTSP). In the GTSP, the set of nodes is partitioned into subsets, called clusters. We must choose exactly one node from each cluster, as well as a route that visits each of the chosen nodes once and returns to the starting node, in order to minimize the total distance traveled. The GTSP therefore combines elements of facility location problems (choosing the nodes) and vehicle routing problems (choosing the route).
Use the following notation. (Do not define any new notation.)
Sets N = set of nodes 
= a cluster,  ; the clusters do not overlap and their union equals N
; the clusters do not overlap and their union equals N
Parameters 
= distance between nodes j and k; assume the distances are symmetric (  )
)Decision Variables 
= 1 if node  is selected to be part of the tour, 0 otherwise
is selected to be part of the tour, 0 otherwise
= 1 if the tour goes directly from node  to node
to node , 0 otherwise
, 0 otherwise- Formulate this problem as a linear discrete optimization problem. Explain the objective function and all constraints in words.
- Propose a construction heuristic for the GTSP. Explain your heuristic briefly.
- Propose an improvement heuristic for the GTSP. Explain your heuristic briefly.
