Chapter 2
Forecasting and Demand Modeling
2.1 Introduction
Demand forecasting is one of the most fundamental tasks that a business must perform. It can be a significant source of competitive advantage by improving customer service levels and by reducing costs related to supply–demand mismatches. In contrast, biased or otherwise inaccurate forecasting results in inferior decisions and thus undermines business performance.
For example, the toy retailer Toys “R” Us made a huge mistake in demand forecasting for the 2015 Christmas season. For several days, the actual number of online orders was more than twice the company's forecasts, and the company's distribution centers were overwhelmed. As a result, the company was forced to throttle demand by terminating some online sales, resulting in lower demand and lower revenue (Ziobro, 2016).
The goal of the forecasting models discussed in this chapter is to estimate the quantity of a product or service that consumers will purchase. Most classical forecasting techniques involve time‐series methods that require substantial historical data. Some of these methods are designed for demands that are stable over time. Others can handle demands that exhibit trends or seasonality, but even these require the trends to be stable and predictable. However, products today have shorter and shorter life cycles, in part driven by rapid technology upgrades for high‐tech products. As a result, firms have much less historical data available to use for forecasting, and any trends that may be evident in historical data may be unreliable for predicting the future.
In this chapter, we first discuss some classical methods for forecasting demand, in Sections 2.2 and 2.3. Next, in Section 2.4, we discuss more recent approaches to forecasting demand using machine learning when we have large quantities of historical data available. In Sections 2.5–2.8, we discuss several methods that can be used to predict demands for new products or products that do not have much historical data. To distinguish these methods from classical time‐series–based methods, we call them demand modeling techniques.
The methods that we discuss in this chapter are quantitative. They all involve mathematical models with parameters that must be calibrated. In contrast, some popular methods for forecasting demand with little or no historical data, such as the Delphi method, rely on experts' qualitative assessments or questionnaires to develop forecasts.
Demand processes may exhibit various forms of nonstationarity over time. These include the following:
- Trends: Demand consistently increases or decreases over time.
- Seasonality: Demand shows peaks and valleys at consistent intervals.
- Product life cycles: Demand goes through phases of rapid growth, maturity, and decline.
Moreover, demands exhibit random error—variations that cannot be explained or predicted—and this randomness is typically superimposed on any underlying nonstationarity.
2.2 Classical Demand Forecasting Methods
Classical forecasting methods use prior demand history to generate a forecast. Some of the methods, such as moving average and (single) exponential smoothing, assume that past patterns of demand will continue into the future, that is, no trend is present. As a result, these techniques are best used for mature products with a large amount of historical data. On the other hand, regression analysis and double and triple exponential smoothing can account for a trend or other pattern in the data. We discuss each of these methods next.
In each of the models that follow, we use ![]() to represent the historical demand data, i.e., the realized demands in periods 1, 2,
to represent the historical demand data, i.e., the realized demands in periods 1, 2, ![]() , t,
, t, ![]() . We also use
. We also use ![]() to denote the forecast of period t's demand that is made in period
to denote the forecast of period t's demand that is made in period ![]() .
.
2.2.1 Moving Average
The moving average method calculates the average amount of demand over a given interval of time and uses this average to predict the future demand. As a result, moving average forecasts work best for demand that has no trend or seasonality. Such demand processes can be modeled as follows:
where I is the mean or “base” demand and ![]() is a random error term.
is a random error term.
A moving average forecast of order N uses the N most recent observed demands. The forecast for the demand in period t is simply given by
That is, the forecast is simply the arithmetic mean of the previous N observations. This is known as a simple moving average forecast of order N.
A generalization of the simple moving average forecast is the weighted moving average, which allows each period to carry a different weight. For instance, if more recent demand is deemed more relevant, then the forecaster can assign larger weights to recent demands than to older ones. If ![]() is the weight placed on the demand in period i, then the weighted moving average forecast is given by
is the weight placed on the demand in period i, then the weighted moving average forecast is given by

Typically, the weights decrease by 1 in each period: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2.2.2 Exponential Smoothing
Exponential smoothing is a technique that uses a weighted average of all past data as the basis for the forecast. It gives more weight to recent information and smaller weight to observations in the past. Single exponential smoothing assumes that the demand process is stationary. Double exponential smoothing assumes that there is a trend, while triple exponential smoothing accounts for both trends and seasonality. These methods all require user‐specified parameters that determine the relative weights placed on recent and older observations when predicting the demand, trend, and seasonality. These three weights are called, respectively, the smoothing factor, the trend factor, and the seasonality factor. We discuss each of these three methods next.
2.2.2.1 Single Exponential Smoothing
Define ![]() as the smoothing constant. Then, we can express the current forecast as the weighted average of the previous forecast and most recently observed demand value:
as the smoothing constant. Then, we can express the current forecast as the weighted average of the previous forecast and most recently observed demand value:
Note that ![]() is the weight placed on the demand observation and
is the weight placed on the demand observation and ![]() is the weight placed on the last forecast. Typically, we place more weight on the previous forecast, so
is the weight placed on the last forecast. Typically, we place more weight on the previous forecast, so ![]() is closer to 0 than to 1.
is closer to 0 than to 1.
Since each forecast depends on the previous forecast, we need a way to get the process started. One simple way to do this is to set ![]() . Note that this method requires one historical demand observation
. Note that this method requires one historical demand observation ![]() ; the first “real” forecast, i.e., the first forecast that uses 2.4, is
; the first “real” forecast, i.e., the first forecast that uses 2.4, is ![]() .
.
Using 2.4, we can write
so
We can continue the substitution in this way and eventually obtain
where ![]() . The single exponential smoothing forecast includes all past observations, but since
. The single exponential smoothing forecast includes all past observations, but since ![]() for
for ![]() , the weights are decreasing as we move backward in time, as illustrated in Figure 2.1. Moreover,
, the weights are decreasing as we move backward in time, as illustrated in Figure 2.1. Moreover,
by (C.50) in Appendix C. These weights can be approximated with an exponential function ![]() . This is why this method is called exponential smoothing.
. This is why this method is called exponential smoothing.

Figure 2.1 Weight distribution for single exponential smoothing.
2.2.2.2 Double Exponential Smoothing
Double exponential smoothing can be used to forecast demands with a linear trend. Such demands can be modeled as follows:
where I is the base demand, S is the slope of the trend in the demand, and ![]() is an error term. The forecast for the demand in period t is the sum of two separate estimates from period
is an error term. The forecast for the demand in period t is the sum of two separate estimates from period ![]() : one of the base signal (the value of the demand process) and one of the slope. That is,
: one of the base signal (the value of the demand process) and one of the slope. That is,
where ![]() is the estimate of the base signal and
is the estimate of the base signal and ![]() is the estimate of the slope, both made in period
is the estimate of the slope, both made in period ![]() .
. ![]() represents our estimate of where the demand process fell in period
represents our estimate of where the demand process fell in period ![]() ; in period t, the process will be
; in period t, the process will be ![]() units greater. The estimates of the base signal and slope are calculated as follows:
units greater. The estimates of the base signal and slope are calculated as follows:
where ![]() is the smoothing constant and
is the smoothing constant and ![]() is the trend constant. Equation 2.7 is similar to 2.4 for single exponential smoothing in the sense that
is the trend constant. Equation 2.7 is similar to 2.4 for single exponential smoothing in the sense that ![]() is the weight placed on the most recent actual demand
is the weight placed on the most recent actual demand ![]() and
and ![]() is the weight on the previous forecast. Equation 2.8 can be explained similarly: It places a weight of
is the weight on the previous forecast. Equation 2.8 can be explained similarly: It places a weight of ![]() on the most recent estimate of the slope (obtained by taking the difference between the two most recent base signals) and a weight of
on the most recent estimate of the slope (obtained by taking the difference between the two most recent base signals) and a weight of ![]() on the previous estimate. Note that, if the trend is downward‐sloping, then
on the previous estimate. Note that, if the trend is downward‐sloping, then ![]() will (usually) be negative.
will (usually) be negative.
As with single exponential smoothing, we need a way to initialize the process. This time, we need two historical demand observations to initialize the forecasts, and we typically set ![]() and
and ![]() (then
(then ![]() ). The first “real” forecast (using 2.7–2.8 to get values for 2.6) is
). The first “real” forecast (using 2.7–2.8 to get values for 2.6) is ![]() .
.
This particular version of double exponential smoothing is also known as Holt's method (Holt, 1957).
2.2.2.3 Triple Exponential Smoothing
Triple exponential smoothing can be used to forecast demands that exhibit both trend and seasonality. Seasonality means that the demand series has a pattern that repeats every N periods for some fixed N. N consecutive periods are called a season. (If the demand pattern repeats every year, for example, then a season is one year. This is different from the common usage of the word “season,” which would refer to a portion of the year.)
To model the seasonality, we use a parameter ![]() ,
, ![]() to represent the ratio between the average demand in period t and the overall average. (Thus,
to represent the ratio between the average demand in period t and the overall average. (Thus, ![]() .) For example, if
.) For example, if ![]() , then on average, the demand in period 6 is 12% below the overall average demand. The
, then on average, the demand in period 6 is 12% below the overall average demand. The ![]() are called seasonal factors. We assume that the seasonal factors are unknown but that they are the same every season. The demand process can be modeled as follows:
are called seasonal factors. We assume that the seasonal factors are unknown but that they are the same every season. The demand process can be modeled as follows:
where I is the value of base signal at time 0, S is the true slope, and ![]() is a random error term. (See Figure 2.2.)
is a random error term. (See Figure 2.2.)

Figure 2.2 Random demands with trend and seasonality.
The forecast for period t is given by
where ![]() and
and ![]() are the estimates of the base signal and slope in period
are the estimates of the base signal and slope in period ![]() and
and ![]() is the estimate of the seasonal factor one season ago.
is the estimate of the seasonal factor one season ago.
The idea behind smoothing with trend and seasonality is basically to “de‐trend” and “de‐seasonalize” the time series by separating the base signal from the trend and seasonality effects. The method uses three smoothing parameters, ![]() ,
, ![]() , and
, and ![]() , in estimating the base signal, the trend, and the seasonality, respectively:
, in estimating the base signal, the trend, and the seasonality, respectively:
Equations 2.11 and 2.12 are very similar to 2.7 and 2.8 for double exponential smoothing, except that 2.11 uses the deseasonalized demand observation, ![]() , instead of
, instead of ![]() , to average it with the current forecast. In 2.13,
, to average it with the current forecast. In 2.13, ![]() is our estimate of the base signal, so
is our estimate of the base signal, so ![]() is our estimate of
is our estimate of ![]() based on the most recent demand. This is averaged with our previous estimate of
based on the most recent demand. This is averaged with our previous estimate of ![]() (made N periods ago) using weighting factor
(made N periods ago) using weighting factor ![]() .
.
Initializing triple exponential smoothing is a bit trickier than for single or double exponential smoothing. To do so, we usually need at least two entire seasons' worth of data (![]() periods), which will be used for the initialization phase. One common method is to initialize the slope as
periods), which will be used for the initialization phase. One common method is to initialize the slope as
In other words, we take the per‐period increase in demand between periods 1 and ![]() , and the per‐period increase between periods 2 and
, and the per‐period increase between periods 2 and ![]() , and so on; and then we take the average over those N values. To initialize the seasonal factors
, and so on; and then we take the average over those N values. To initialize the seasonal factors ![]() , we estimate the seasonal factor for each period in the first two seasons, and then average them over those two seasons to obtain the initial seasonal factors:
, we estimate the seasonal factor for each period in the first two seasons, and then average them over those two seasons to obtain the initial seasonal factors:

for ![]() . Each denominator is the average demand in one season of the available data, so the fractions in the parentheses estimate the seasonal factor for the tth period in each season. The right‐hand side as a whole averages these estimates over the two seasons. Finally, we estimate the base signal as
. Each denominator is the average demand in one season of the available data, so the fractions in the parentheses estimate the seasonal factor for the tth period in each season. The right‐hand side as a whole averages these estimates over the two seasons. Finally, we estimate the base signal as ![]() . The first “real” forecast is
. The first “real” forecast is ![]() .
.
This method is also sometimes known as Winters's method or the Holt–Winters method (Winters, 1960).
2.2.3 Linear Regression
Historical data can also be used to forecast demands by determining a cause–effect relationship between some independent variables and the demand. For instance, the demand for sales of a brand of laptop computer may heavily depend on the sales price and the features. A regression model can be developed which describes this relationship. The model can then be used to forecast the demand for laptops with a given price and a given set of features.
In linear regression, the model specification assumes that the dependent variable, Y, is a linear combination of the independent variables. For example, in simple linear regression, there is one independent variable, X, and two parameters, ![]() and
and ![]() :
:
Here, X and Y are random variables. For any given pair of observed variables x and y, we have
where ![]() is a random error term. The objective of regression analysis is to estimate the parameters
is a random error term. The objective of regression analysis is to estimate the parameters ![]() and
and ![]() .
.
To build a regression model, we need historical data points—observations of both the independent variable(s) and the dependent variable. Let ![]()
![]() be n paired data observations for a simple linear regression model. The goal is to find values of
be n paired data observations for a simple linear regression model. The goal is to find values of ![]() and
and ![]() so that the line defined by 2.16 gives the best fit of the data. In particular,
so that the line defined by 2.16 gives the best fit of the data. In particular, ![]() and
and ![]() are chosen to minimize the sum of the squared residuals, where the residual for data point i is defined as the difference between the observed value of
are chosen to minimize the sum of the squared residuals, where the residual for data point i is defined as the difference between the observed value of ![]() and the predicted value of
and the predicted value of ![]() obtained by substituting
obtained by substituting ![]() in 2.16. That is, we want to solve
in 2.16. That is, we want to solve
where ![]() is the residual for data point i. The optimal values of
is the residual for data point i. The optimal values of ![]() and
and ![]() are given by
are given by
where ![]() and
and ![]() are the sample means of the
are the sample means of the ![]() and
and ![]() , respectively;
, respectively; ![]() is the sample correlation coefficient between x and y; and
is the sample correlation coefficient between x and y; and ![]() and
and ![]() are the sample standard deviations of x and y, respectively (see, e.g., Tamhane and Dunlop (1999)).
are the sample standard deviations of x and y, respectively (see, e.g., Tamhane and Dunlop (1999)).
If the demands exhibit a linear trend over time, then we can use regression analysis to forecast the demand using the time period itself (rather than, say, price or features) as the independent variable. In this case, it can be shown (see, e.g., Nahmias (2005, Appendix 2‐B)) that the optimal values of ![]() and
and ![]() are given by:
are given by:
where ![]() are the observed demands and
are the observed demands and
According to the comparison by Carbonneau et al. (2008), linear regression often achieves better performance than moving average and trend methods.
2.3 ForecastAccuracy
2.3.1 MAD, MSE, and MAPE
At some point after a forecast is computed, the actual demand is observed, providing us with an opportunity to evaluate the quality of the forecast. The most basic measure of the forecast accuracy is the forecast error, denoted ![]() , which is defined as the difference between the forecast for period t and the actual demand for that period:
, which is defined as the difference between the forecast for period t and the actual demand for that period:
where ![]() is a forecast obtained using any method and
is a forecast obtained using any method and ![]() is the actual observed demand.
is the actual observed demand.
Since the forecast and the demand are random variables, so is the forecast error; let ![]() and
and ![]() denote its mean and variance, respectively. If the mean of the forecast error,
denote its mean and variance, respectively. If the mean of the forecast error, ![]() , equals 0, we say the forecasting method is unbiased: It does not produce forecasts that are systematically either too low or too high. However, even an unbiased forecasting method can still be very inaccurate. One way to measure the accuracy is using the variance of the forecast error,
, equals 0, we say the forecasting method is unbiased: It does not produce forecasts that are systematically either too low or too high. However, even an unbiased forecasting method can still be very inaccurate. One way to measure the accuracy is using the variance of the forecast error, ![]() . To compute
. To compute ![]() or
or ![]() , however, we need to know the probabilistic process that underlies both the demands and the forecasts. Typically, therefore, we use performance measures based on sample quantities rather than population quantities.
, however, we need to know the probabilistic process that underlies both the demands and the forecasts. Typically, therefore, we use performance measures based on sample quantities rather than population quantities.
Two of the most common such measures are the mean absolute deviation (MAD) and the mean squared error (MSE), defined as follows:
MSE is identical to the sample variance of the random forecast error ![]() except for the denominator of the coefficient. MAD is sometimes preferred to MSE in real applications because it avoids the calculation of squaring, though modern spreadsheet and statistics packages can compute either performance measure easily. When the forecast errors are normally distributed, their standard deviation is often estimated as
except for the denominator of the coefficient. MAD is sometimes preferred to MSE in real applications because it avoids the calculation of squaring, though modern spreadsheet and statistics packages can compute either performance measure easily. When the forecast errors are normally distributed, their standard deviation is often estimated as
This is useful when ![]() is required (e.g., for inventory optimization models—see Section 4.3.2.7), since, as previously noted, we do not typically know
is required (e.g., for inventory optimization models—see Section 4.3.2.7), since, as previously noted, we do not typically know ![]() directly.
directly.
Note that both MAD and MSE are dependent on the magnitude of the values of demand; if we express the demands in different units (e.g., tons vs. pounds), the performance measures will change. By comparison, the mean absolute percentage error (MAPE) is independent of the magnitude of the demand values:
Table 2.2
Demands (![]() ), forecasts (
), forecasts (![]() ), and forecast errors (
), and forecast errors (![]() ) for An Inventory Story, periods 13–24, for Example 2.6.
) for An Inventory Story, periods 13–24, for Example 2.6.
| Moving | Exponential | ||||
| Average | Smoothing | ||||
| t |
|
|
|
|
|
| 13 | 10.98 | 9.80 | ‐1.18 | 9.98 | ‐1.00 |
| 14 | 12.07 | 10.01 | ‐2.06 | 10.18 | ‐1.89 |
| 15 | 11.45 | 10.63 | ‐0.82 | 10.56 | ‐0.89 |
| 16 | 9.39 | 10.88 | 1.49 | 10.74 | 1.35 |
| 17 | 10.59 | 10.57 | ‐0.02 | 10.47 | ‐0.12 |
| 18 | 8.43 | 10.90 | 2.47 | 10.49 | 2.06 |
| 19 | 11.78 | 10.39 | ‐1.39 | 10.08 | ‐1.70 |
| 20 | 7.71 | 10.33 | 2.62 | 10.42 | 2.71 |
| 21 | 7.86 | 9.58 | 1.72 | 9.88 | 2.02 |
| 22 | 8.38 | 9.27 | 0.89 | 9.47 | 1.09 |
| 23 | 4.11 | 8.83 | 4.72 | 9.26 | 5.15 |
| 24 | 12.88 | 7.97 | ‐4.91 | 8.23 | ‐4.65 |
| MAD | 2.02 | 2.05 | |||
| MSE | 6.13 | 6.26 | |||
| MAPE | 25.97 | 26.85 | |||
2.3.2 Forecast Errors for Moving Average and Exponential Smoothing
Assume that the demand is generated by the process
where ![]() . Since the demand process is stationary, either moving average or exponential smoothing is an appropriate forecasting method.
. Since the demand process is stationary, either moving average or exponential smoothing is an appropriate forecasting method.
In a moving average of order N, the forecast ![]() is given by 2.2. It follows that
is given by 2.2. It follows that

Therefore, moving‐average forecasts are unbiased when the demand is stationary.
We can also derive the variance of the forecast error, which can be expressed as

Note that the second equality uses the fact that the forecast and demand in period t are statistically independent.
If forecasts are instead performed using exponential smoothing, one can show (see Problem 2.12) that
2.4 Machine Learning in Demand Forecasting
2.4.1 Introduction
We are in the age of big data. The huge volume of data generated every day, the high velocity of data creation, and the large variety of sources all make today's business information environment different than it was only a decade ago. Using data intelligently is key to business decision‐making. A 2012 Harvard Business Review article notes: “Data‐driven decisions are better decisions—it's as simple as that. Using big data enables managers to decide on the basis of evidence rather than intuition. For that reason it has the potential to revolutionize management” (McAfee and Brynjolfsson, 2012).
Fortunately, many businesses have access to large volumes of historical demand data that can help when forecasting future demands. In this section, we introduce some of the main machine learning techniques for demand forecasting. Compared with classical forecasting methods such as the time series methods discussed in Section 2.2, machine learning models often significantly increase prediction accuracy.
2.4.2 Machine Learning
In general, machine learning (ML) refers to a set of algorithms that can learn from and make predictions about data. These algorithms take data as inputs and generate predictions or decisions as outputs. Machine learning is closely related to statistical learning, which refers to a set of tools for modeling and understanding complex data sets (James et al. 2013). Machine learning and statistical learning have developed rapidly in recent years. Both techniques fall into the overall field of data science, which covers a wider range of topics, including database design and data visualization techniques.
One category of ML algorithms is called supervised learning, in which the historical data contain both inputs and outputs, and the learning algorithm learns to predict an output for a given set of inputs. For example, we might have historical data that contains the outdoor temperature and the number of glasses of lemonade that were sold on each day. The learning algorithm tries to infer the relationship between the two, so that for a given temperature, it can predict the number of glasses of lemonade that will be sold. Regression is a simple example. In contrast, unsupervised learning explores relationships and structures within the data without any known “ground truth” labels or outputs. For example, if we wish to partition consumers into market segments, we might use a clustering algorithm, which is a type of unsupervised learning. (See Friedman et al. (2001) or James et al. (2013) for further discussion of this dichotomy.) Demand forecasting falls into the category of supervised learning since we need to predict future demands (outputs) using historical demand data and other market information (inputs).
Common supervised learning methods include linear regression (and its nonlinear extensions), kernel methods, tree‐based models, support vector machines (SVMs), and neural networks. Graphical models involving hidden Markov models (or, in their simplest form, mixture models) and Markov random fields also receive considerable attention. In the following subsections, we discuss the learning methods that are most commonly applied to demand forecasting.
2.4.2.1 Linear Regression
Linear regression is a very simple supervised learning method. It assumes that the output Y is linear in the inputs ![]() , where p is the number of distinct input variables (also called predictors or features):
, where p is the number of distinct input variables (also called predictors or features):
For particular values of the inputs and outputs, we have
where ![]() is a random error term. The
is a random error term. The ![]() s are coefficients that need to be estimated from data. If
s are coefficients that need to be estimated from data. If ![]() , then we have simple linear regression, which we discuss in Section 2.2.3. (In Section 2.2.3, we focused on the use of time as the independent variable in order to predict demands as a function of time. Here, our independent variables can be any feature.)
, then we have simple linear regression, which we discuss in Section 2.2.3. (In Section 2.2.3, we focused on the use of time as the independent variable in order to predict demands as a function of time. Here, our independent variables can be any feature.)
The most common way to obtain the ![]() s is least squares, which seeks to find the minimizer of the sum of the squares of the residuals. (Recall from Section 2.2.3 that the residual for data point i is the difference between the observed and predicted values of
s is least squares, which seeks to find the minimizer of the sum of the squares of the residuals. (Recall from Section 2.2.3 that the residual for data point i is the difference between the observed and predicted values of ![]() .) The derived estimated coefficients are denoted
.) The derived estimated coefficients are denoted ![]() . Then we can make predictions on new inputs by using
. Then we can make predictions on new inputs by using
where ![]() is our predicted value for the output, given the observed values
is our predicted value for the output, given the observed values ![]() of the inputs.
of the inputs.
Although the linear regression model assumes a linear relationship between the output and the inputs, we can model nonlinear relationships by introducing basis functions and splines. When the number of predictors is large, we can utilize shrinkage methods such as least absolute shrinkage and selection operator (LASSO) and ridge regression. In general, linear regression is a simple but strong learning method.
2.4.2.2 Tree‐based models
Tree‐based models use decision trees to make predictions for a given set of inputs. They can be applied both to regression problems (in which the outputs are continuous) and to classification problems (in which the outputs are categorical). The trees used for these two types of problems are referred to as regression trees and classification trees, respectively. In demand forecasting, regression trees have received more attention because of their simplicity and interpretability.
A regression tree divides the space of input variables, i.e., the set of possible values of ![]() , into distinct and nonoverlapping regions and assigns a single output,
, into distinct and nonoverlapping regions and assigns a single output, ![]() , to each region k. If a given input
, to each region k. If a given input ![]() falls into region k, then the demand forecast y for that input is equal to
falls into region k, then the demand forecast y for that input is equal to ![]() . The
. The ![]() values are determined simply by averaging the observations in the historical data that fall into that region.
values are determined simply by averaging the observations in the historical data that fall into that region.
The goal is to choose the partition strategy that minimizes the sum of squares of the residuals, similar to linear regression. However, in practice, the number of possible partitions may be too large to enumerate. Therefore, it is common to use a binary splitting method called recursive partitioning, which generates two regions from the original region at each iteration. For the purposes of prediction, the size of the tree is limited by a pruning process. A single tree may not perform well due to high variance of the forecast, so researchers have developed methods that combine several trees to enhance the prediction performance. These include random forests, bagging, and boosting.
Tree‐based models are used widely in demand forecasting for many industries. For example, Ferreira et al. (2015) apply regression trees with bagging to predict the demand of new styles for an online retailer. They show that tree‐based models outperform linear regression and some nonlinear regression models consistently. Ali et al. (2009) develop regression trees to predict stock‐keeping unit (SKU) sales for a European grocery retailer. They incorporate information about current promotions when constructing regression trees and show that regression trees provide better accuracy than linear regression and SVMs.
2.4.2.3 Support vector machines
SVMs are designed to partition the space of input variables into two regions, i.e., to make a binary prediction about a given output based on which region a given input vector falls into. The partition is accomplished by finding a separating hyperplane. In particular, assuming that the training data set is linearly separable, the optimal separating hyperplane is found by solving the following optimization problem:
where N is the number of observations, ![]() is the binary output (
is the binary output (![]() ) for observation i,
) for observation i, ![]() is the vector of input variables for observation i, and
is the vector of input variables for observation i, and ![]() denotes dot product. This is also called a maximum margin classifier, where the margin is defined as
denotes dot product. This is also called a maximum margin classifier, where the margin is defined as ![]() . The optimal values of the vector
. The optimal values of the vector ![]() and the scalar
and the scalar ![]() characterize the separating hyperplane. For a given input vector
characterize the separating hyperplane. For a given input vector ![]() , we predict an output value of 1 if
, we predict an output value of 1 if ![]() and a value of 0 otherwise.
and a value of 0 otherwise.
For example, suppose we wish to predict which customers will purchase a product based on their age, income, and money spent at the store in the past year. We code each customer in the historical data with a 1 or 0 depending on whether they purchased the product, then solve 2.36–2.37 to find the hyperplane that does the best job of separating the 1s from the 0s. For each new customer, we simply calculate ![]() and make a prediction accordingly.
and make a prediction accordingly.
SVMs can be generalized to allow nonlinearities by mapping the input space into a high‐dimensional space using kernel functions. In essence, this allows the region to be partitioned using a surface that is not linear, i.e., is not a hyperplane. Popular choices of kernel functions include polynomials and radial basis functions (RBFs).
Since SVMs can be used to make binary predictions, they can be used to predict whether a given customer will purchase a product. They can also be used to forecast the demand as a quantity using support vector regression (SVR), an adaptation of the SVM approach to regression problems using kernel functions. SVR is among the best machine learning methods for supply chain demand forecasting (Carbonneau et al., 2008).
2.4.2.4 Neural Networks
A neural network consists of several nodes, also called neurons, arranged into layers. The first layer of nodes represents the inputs (the ![]() values); the last layer represents the outputs (the Y value); and one or more layers in between, called hidden layers, process the information from the input layer and perform the actual computation of the network. (See Figure 2.5.) Neural networks have been used extensively for classification problems such as image and speech processing, where the goal is to determine what sort of physical or linguistic object the inputs represent. But neural networks can and have been successfully applied to regression‐type problems such as demand forecasting.
values); the last layer represents the outputs (the Y value); and one or more layers in between, called hidden layers, process the information from the input layer and perform the actual computation of the network. (See Figure 2.5.) Neural networks have been used extensively for classification problems such as image and speech processing, where the goal is to determine what sort of physical or linguistic object the inputs represent. But neural networks can and have been successfully applied to regression‐type problems such as demand forecasting.
The central idea behind neural networks is that in each layer (except the first), we extract linear combinations of the inputs from the previous layer as derived features, and then model the output as a nonlinear function of these features. For example, in a typical network with a single hidden layer with M nodes, each hidden‐layer node ![]() calculates the derived feature
calculates the derived feature
where ![]() is the vector of inputs,
is the vector of inputs, ![]() is a scalar,
is a scalar, ![]() is a vector with p elements (one per input feature), and
is a vector with p elements (one per input feature), and ![]() is a nonlinear function called the activation function. Note that the term inside the
is a nonlinear function called the activation function. Note that the term inside the ![]() is a linear combination of the inputs plus a constant. Typical activation functions include the sigmoid function and the ReLU function. The
is a linear combination of the inputs plus a constant. Typical activation functions include the sigmoid function and the ReLU function. The ![]() are also called hidden units since they are not directly observed. Once the hidden units are calculated by the hidden‐layer nodes, the output Y is modeled as a function of the hidden units:
are also called hidden units since they are not directly observed. Once the hidden units are calculated by the hidden‐layer nodes, the output Y is modeled as a function of the hidden units:
where ![]() is a (possibly nonlinear) function.
is a (possibly nonlinear) function.
The key challenge in fitting a neural network model is the determination of the weights ![]() and
and ![]() . This is usually done using some sort of algorithm that modifies the weights as the network “learns” right and wrong answers. The most common such algorithm is known as backpropagation, which calculates gradients with respect to the weights; another method (such as gradient descent) is then used to update the weights. Determining these weights—sometimes referred to as training the network—can be computationally intensive. However, once the network is trained, generating an output value for a new set of inputs is extremely efficient. (For further details, see, e.g., Friedman et al. (2001).)
. This is usually done using some sort of algorithm that modifies the weights as the network “learns” right and wrong answers. The most common such algorithm is known as backpropagation, which calculates gradients with respect to the weights; another method (such as gradient descent) is then used to update the weights. Determining these weights—sometimes referred to as training the network—can be computationally intensive. However, once the network is trained, generating an output value for a new set of inputs is extremely efficient. (For further details, see, e.g., Friedman et al. (2001).)

Figure 2.5 A simple neural network.
Some neural networks contain multiple hidden layers, not just one; this can improve the accuracy of the network's predictions but makes the network harder to train. Such deep neural networks have led to huge advances in machine learning, with great successes not only in classification and prediction problems such as image processing and demand forecasting, but also, when coupled with reinforcement learning (RL), in solving decision problems such as those in board games; one famous example is Google DeepMind's AlphaGo program, which beat the world‐champion (human) Go player in 2016.
Carbonneau et al. (2008) test two different types of neural networks on demand forecasting and conclude that neural networks perform better than traditional methods. Venkatesh et al. (2014) combine neural networks with clustering to predict demand for cash at automatic teller machines (ATMs). They find that their model increases the prediction accuracy substantially.
2.5 Demand Modeling Techniques
As the pace of technology accelerates, companies are introducing new products faster and faster to stay competitive. There is a diffusion process associated with the demand for any new product, so companies need to plan the timing and quantity of new product releases carefully to match supply and demand as closely as possible. To do so, they need to understand the life cycles and demand dynamics of their products.
One of the authors has worked with a high‐tech company in China. The company was complaining about their very inaccurate demand forecasts, which led to excess inventory valued at approximately $25 million. The author was invited to give lectures on demand forecasting and inventory management. The first day's lecture focused on the classical time‐series demand forecasting techniques discussed earlier in this chapter. The reaction from the company's forecasting team was lukewarm. They were already quite familiar with these techniques and had tried hard to make them work, unsuccessfully. It turns out that classical forecasting techniques did not work well with the company's highly variable, short‐life‐cycle products, so the firm introduced products at the wrong times in the wrong quantities. The forecasting team's reaction was quite different when the author discussed the Bass diffusion model, the leading‐indicator method, and choice models, which are designed to account for short life cycles and other important factors. We discuss each of these methods in detail in the following sections. (As a postscript, the company reported more than a 50% increase in sales about one and a half years after they improved their forecasting techniques, partially due to the fact that money was being invested in a better mix of products.)
2.6 Bass Diffusion Model
The sales patterns of new products typically go through three phases: rapid growth, maturity, and decline. The Bass diffusion model (Bass, 1969) is a well‐known parametric approach for estimating the demand trajectory of a single new product over time. Bass's basic three‐parameter model has proved to be very effective in delivering accurate forecasts and insights for a huge variety of new product introductions, regardless of pricing and advertising decisions. The model forecasts well even when limited or no historical data are available. For example, Figure 2.6 depicts demand data (forecast and actual) for the introduction of color television sets in the 1960s.

Figure 2.6 Color TVs in the 1960s: Forecasts from Bass model and actual demands..
Reprinted by permission, Bass, Empirical generalizations and marketing science: A personal view, Marketing Science, 14(3), 1995, G6–G19. ©1995, the Institute for Operations Research and the Management Sciences (INFORMS), 7240 Parkway Drive, Suite 300, Hanover, MD 21076 USA
The premise of the Bass model is that customers can be classified into innovators and imitators. Innovators (or early adopters) purchase a new product without regard to the decisions made by other individuals. Imitators, on the other hand, are influenced in the timing of their purchases by previous buyers through word‐of‐mouth communication. Refer to Figure 2.7 for an illustration. The number of innovators decreases over time, while the number of imitators purchasing the product first increases, and then decreases. The goal of the Bass model is to characterize this behavior in an effort to forecast the demand. It mathematically characterizes the word‐of‐mouth interaction between those who have adopted the innovation and those who have not yet adopted it. Moreover, it attempts to predict two important dimensions of a forecast: how many customers will eventually adopt the new product, and when they will adopt. Knowing the timing of adoptions is important as it can guide the firm to smartly utilize resources in marketing the new product. Our analysis of this model is based on that of Bass (1969).

Figure 2.7 Bass diffusion curve.
2.6.1 The Model
The Bass model assumes that ![]() , the probability that a given buyer makes an initial purchase at time t given that she has not yet made a purchase, is a linear function of the number of previous buyers; that is,
, the probability that a given buyer makes an initial purchase at time t given that she has not yet made a purchase, is a linear function of the number of previous buyers; that is,
where ![]() is the cumulative demand by time t. Equation 2.40 suggests that two factors will influence the probability that a customer makes a purchase at time t. The first factor is the coefficient of innovation, denoted p, which is a constant, independent of how many other customers have adopted the innovation before time t. The second factor,
is the cumulative demand by time t. Equation 2.40 suggests that two factors will influence the probability that a customer makes a purchase at time t. The first factor is the coefficient of innovation, denoted p, which is a constant, independent of how many other customers have adopted the innovation before time t. The second factor, ![]() , measures the “contagion” effect between the innovators and the imitators and is proportional to the number of customers who have already adopted by time t. The parameters q and m represent the coefficient of imitation and the market size, respectively. We require
, measures the “contagion” effect between the innovators and the imitators and is proportional to the number of customers who have already adopted by time t. The parameters q and m represent the coefficient of imitation and the market size, respectively. We require ![]() . In fact, usually
. In fact, usually ![]() ; for example,
; for example, ![]() and
and ![]() have been reported as average values (Sultan et al., 1990).
have been reported as average values (Sultan et al., 1990).
We assume that the time index, t, is measured in years. Of course, any time unit is possible, but the values we report for p and q implicitly assume that t is measured in years.
Let ![]() be the derivative of
be the derivative of ![]() , i.e., the demand rate at time t. Using Bayes' rule, one can show that
, i.e., the demand rate at time t. Using Bayes' rule, one can show that
(See Section 2.6.2 for a derivation of the analogous equation in the discrete‐time model.) Combining 2.40 and 2.41, we have
Our goal is to characterize ![]() so that we can understand how the demand evolves over time. To a certain extent, 2.42 does this, but 2.42 is a differential equation; it expresses
so that we can understand how the demand evolves over time. To a certain extent, 2.42 does this, but 2.42 is a differential equation; it expresses ![]() in terms of its derivative. Our preference would be to have a closed‐form expression for
in terms of its derivative. Our preference would be to have a closed‐form expression for ![]() . Fortunately, this is possible:
. Fortunately, this is possible:
As a corollary, one can determine the time at which the demand rate peaks, and the demand rate and cumulative demand at that point:
If p is very small, then the demand growth occurs slowly, whereas if p and q are large, sales take off rapidly and fall off quickly after reaching their maximum. Note that the formulas in Corollary 2.1 are only well defined if ![]() , which we previously assumed to be true. If, instead,
, which we previously assumed to be true. If, instead, ![]() , then the innovation effects will dominate the imitation effects, and the peak demand will occur immediately upon the introduction of the product and will decline thereafter. In summary, by varying the values of p and q, we can represent many different patterns of demand diffusion.
, then the innovation effects will dominate the imitation effects, and the peak demand will occur immediately upon the introduction of the product and will decline thereafter. In summary, by varying the values of p and q, we can represent many different patterns of demand diffusion.
Seasonal influence factors can be incorporated into the Bass framework. Kurawarwala and Matsuo (1996) present a growth model to forecast demand for short‐life‐cycle products that is motivated by the Bass diffusion model. They use ![]() to denote the seasonal influence parameter at time t, given as a function with a periodicity of 12 months. Their proposed seasonal growth model is characterized by the following differential equation:
to denote the seasonal influence parameter at time t, given as a function with a periodicity of 12 months. Their proposed seasonal growth model is characterized by the following differential equation:
where ![]() is the cumulative demand by time t (
is the cumulative demand by time t (![]() ),
), ![]() is its derivative, and m, p, and q are the scale and shape parameters, which are analogous to the parameters in the Bass diffusion model. This is identical to 2.42 except for the multiplier
is its derivative, and m, p, and q are the scale and shape parameters, which are analogous to the parameters in the Bass diffusion model. This is identical to 2.42 except for the multiplier ![]() .
.
Integrating 2.48, we get the cumulative demand ![]() as follows:
as follows:
When ![]() for all t, 2.49 reduces to 2.43 from Bass's original model.
for all t, 2.49 reduces to 2.43 from Bass's original model.
2.6.2 Discrete‐Time Version
A discrete‐time version of the Bass model is available. In this case, ![]() represents the demand in period t, and
represents the demand in period t, and ![]() represents the cumulative demand up to period t. Let
represents the cumulative demand up to period t. Let ![]() be the probability that a customer buys the product in period t given that she did not buy it in periods
be the probability that a customer buys the product in period t given that she did not buy it in periods ![]() . Bayes' rule says that
. Bayes' rule says that
Here, let A represent “customer buys in t” and B represent “customer didn't buy in ![]() .” Then
.” Then

(Note the similarity to 2.41, which is for continuous time.) Then the discrete‐time analogue of 2.42 is
where ![]() .
.
2.6.3 Parameter Estimation
The Bass model is heavily driven by the parameters m, p, and q. In this section, we briefly discuss how these parameters may be estimated.
If historical data are available, we can estimate the parameters p, q, and m by first finding the least‐squares estimates of the parameters a, b, and c in the following linear regression model:
Note that this model uses the discrete‐time version of the Bass model (in which we observe demands ![]() and calculate cumulative demands
and calculate cumulative demands ![]() ) since, in practice, we observe discrete demand quantities rather than a continuous demand function. After finding a, b, and c using standard regression analysis, the parameters of the Bass model can be determined as follows:
) since, in practice, we observe discrete demand quantities rather than a continuous demand function. After finding a, b, and c using standard regression analysis, the parameters of the Bass model can be determined as follows:
However, because the Bass model is typically used for new products, in most cases historical data are not available to estimate the parameters. Instead, m is typically estimated qualitatively, using judgment or intuition from management about the size of the market, market research, or the Delphi method. In some markets these estimates can be rather precise. For instance, the pharmaceutical industry is known for their accurate demand estimates, which derive from abundant data regarding the incidence of diseases and ailments (Lilien et al., 2007). The parameters p and q tend to be relatively consistent within a given industry, so these can often be estimated from the diffusion patterns of similar products. Lilien and Rangaswamy (1998) provide industry‐specific data for a wide range of industries. (See Table 2.4 for some examples.)
Table 2.4 Bass model parameters. Adapted with permission from Lilien and Rangaswamy, Marketing Engineering: Computer‐Assisted Marketing Analysis and Planning, Addison‐Wesley, with permission obtained from Pearson, 1998, p. 201.
| Product | p | q |
| Cable TV | 0.100 | 0.060 |
| Camcorder | 0.044 | 0.304 |
| Cellular phone | 0.008 | 0.421 |
| CD player | 0.157 | 0.000 |
| Radio | 0.027 | 0.435 |
| Home PC | 0.121 | 0.281 |
| Hybrid corn | 0.000 | 0.797 |
| Tractor | 0.000 | 0.234 |
| Ultrasound | 0.000 | 0.534 |
| Dishwasher | 0.000 | 0.179 |
| Microwave | 0.002 | 0.357 |
| VCR | 0.025 | 0.603 |
2.6.4 Extensions
After more than half a century, the Bass model is still actively used in demand forecasting and production planning. Sultan et al. (1990), Mahajan et al. (1995), and Bass (2004) provide broad overviews of these applications. The original model has also been extended in a number of ways. Ho et al. (2002) provide a joint analysis of demand and sales dynamics when the supply is constrained, and thus the usual word‐of‐mouth effects are mitigated. Their analysis generalizes the Bass model to include backorders and lost sales and describes the diffusion dynamics when the firm actively makes supply‐related decisions to influence the diffusion process. Savin and Terwiesch (2005) describe the demand dynamics of two new products competing for a limited target market, generalizing the innovation and imitation effects in Bass's original model to account for this competition. Schmidt and Druehl (2005) explore the influence of product improvements and cost reductions on the new‐product diffusion process. Ke et al. (2013) consider the problem of extending a product line while accounting for both inventory (supply) and diffusion (demand). The model determines whether and when to introduce the line extension and the corresponding production quantities. Islam (2014) uses the Bass model (as well as experimental discrete choice data—see Section 2.8) to predict household adoption of photovoltaic (PV) solar cells.
2.7 Leading Indicator Approach
Product life cycles are becoming shorter and shorter, so it is difficult to obtain enough historical data to forecast demands accurately. One idea that has proven to work well in such situations is the use of leading indicators—products that can be used to predict the demands of other, later products because the two products share a similar demand pattern. This approach was introduced by Aytac and Wu (2013) and by Wu et al. (2006), who describe an application of the method at the semiconductor company Agere Systems.
The approach is applied in situations in which a company introduces many related products, such as multiple varieties of semiconductors, cellular phones, or grocery items. The idea is first to group the products into clusters so that all of the products within a cluster share similar attributes. There are several ways to perform this clustering. If one can identify a few demand patterns that all products follow, then it is natural simply to group products sharing the same pattern into the same cluster. For instance, after examining demand data for about 3500 products, Meixell and Wu (2001) find that the products follow six basic demand patterns (i.e., diffusion curves from the Bass model in Section 2.6) and can be grouped into these patterns using statistical cluster analysis. Wu et al. (2006), on the other hand, focus on exogenously defined product characteristics, such as resources, technology group, or sales region, and group the products that have similar characteristics into the same cluster.
The goal is then to identify some potential leading‐indicator products within each cluster. A product is a leading indicator if the demand pattern of this product will likely be approximately repeated later by other products in the same cluster. For example, Figure 2.8 depicts the demand for a leading indicator product (solid line) and the total demand for all of the products in the cluster (dashed line). If the leading indicator curve is shifted to the right by three periods (the “lag”), the two curves share a similar structure. Therefore, the leading indicator product provides some basis for predicting the demand of the rest of the products in the cluster. Even though all of the products are on the market simultaneously, the lag provides enough time so that supply chain planning for the products in the cluster can take place based on the forecasts provided by the leading indicator. Of course, correctly identifying the leading indicator is critical.

Figure 2.8 An example of a leading‐indicator product.
Wu et al. (2006) suggest the following procedure to identify a leading indicator within a given cluster. Let C be the set of products, i.e., the cluster. Each product ![]() will be treated as a potential leading indicator. Suppose we have historical demand data through period T. Let
will be treated as a potential leading indicator. Suppose we have historical demand data through period T. Let ![]() be the observed demand for product i in period t, and let
be the observed demand for product i in period t, and let ![]() be the total demand for the entire cluster in period t,
be the total demand for the entire cluster in period t, ![]() . Then leading indicators can be identified using Algorithm 2.1. In line 4 of the algorithm, the correlation
. Then leading indicators can be identified using Algorithm 2.1. In line 4 of the algorithm, the correlation ![]() measures how well the demand of item i over the time interval
measures how well the demand of item i over the time interval ![]() predicts the demand of the cluster over
predicts the demand of the cluster over ![]() .
.
Once a leading indicator i with time lag k is identified as having a satisfactory correlation coefficient ![]() , we can forecast the demand for the rest of the product cluster using the demand history from the leading indicator as follows:
, we can forecast the demand for the rest of the product cluster using the demand history from the leading indicator as follows:
- Regress the demand time‐series of product cluster C (excluding i) over
 against the time series of the leading indicator over
against the time series of the leading indicator over  using the model (2.54)
using the model (2.54)
and determine the optimal regression parameters
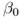 and
and  .
.
- For a given month
 (that is, a month for which we do not have historical data but whose demand we wish to forecast), generate the forecast for the cluster,
(that is, a month for which we do not have historical data but whose demand we wish to forecast), generate the forecast for the cluster,  , using the time series of the leading indicator i from k periods earlier: (2.55)
, using the time series of the leading indicator i from k periods earlier: (2.55)
2.8 Discrete ChoiceModels
2.8.1 Introduction to Discrete Choice
In economics, discrete choice models involve choices between two or more discrete alternatives. For example, a customer chooses which of several competing products to buy; a firm decides which technology to use in production; or a passenger chooses which transportation mode to travel by. The set of choices is assumed to be discrete, and the corresponding models are therefore called discrete choice models. (A related set of models, called continuous choice models, assume that the range of choices is continuous. Although these models are not the focus of our discussion, many of the concepts that we describe below are easily transferable to continuous choice models. In fact, discrete choices generally reveal less information about the choice process than continuous ones, so the econometrics of discrete choice is usually more challenging.)
The idea behind discrete choice models is to build a statistical model that predicts the choice made by an individual based on the individual's own attributes as well as the attributes of the available choices. For example, a student's choice of which college to attend is determined by factors relating to the student, including his or her career goals, scholarly interests, and financial situation, as well as factors relating to the colleges, including their reputations and locations. Choice models attempt to quantify this relationship statistically. Rather than modeling the attributes (career goals, scholarly interests, etc.) as independent variables and then predicting the choice as the dependent variable, choice models are at the aggregate (population) level and assume that each decision‐maker's preferences are captured implicitly by that model.
At first, it may seem that discrete choice models mainly deal with “which”‐type rather than “how many”‐type decisions, unlike the other forecasting and demand‐modeling techniques described in this chapter. However, discrete choice models can be and have been used to forecast quantities, such as the number and duration of phone calls that households make (Train et al., 1987); the demand for electric cars (Beggs et al., 1981) and mobile telephones (Ida and Kuroda, 2009); the demand for planned transportation systems, such as highways, rapid transit systems, and airline routes (Train, 1978; Ramming, 2001; Garrow, 2010)); and the number of vehicles a household chooses to own (McFadden, 1984). Choice models estimate the probability that a person selects a particular alternative. Thus, aggregating the “which” decision across the population will give answers to the “how many” questions and can be very useful for forecasting demand.
Discrete choice models take many forms, including binary and multinomial logit, binary and multinomial probit, and conditional logit. However, there are several features that are common to all of these models. These include the way they characterize the choice set, consumer utility, and the choice probabilities. We briefly describe each of these features next. (See Train (2009) for more details about these features.)
The Choice Set: The choice set is the set of options that are available to the decision‐maker. The alternatives might represent competing products or services, or any other options or items among which the decision‐maker must choose. For a discrete choice model, the set of alternatives in the choice set must be mutually exclusive, exhaustive, and finite. The first two requirements mean that the set must include all possible alternatives (so that the decision‐maker necessarily does make a choice from within the set) and that choosing one alternative means not choosing any others (so one alternative from the set dominates all other options for the decision‐maker). The third requirement distinguishes discrete choice analysis from, say, linear regression analysis in which the dependent variable can (theoretically) take an infinite number of values.
Consumer Utility: Suppose there are N decision‐makers, each of whom must select an alternative from the choice set I. A given decision‐maker n would obtain a certain level of utility from alternative ![]() ; this utility is denoted
; this utility is denoted ![]() . Discrete choice models usually assume that the decision‐maker is a utility maximizer. That is, he will choose alternative i if and only if
. Discrete choice models usually assume that the decision‐maker is a utility maximizer. That is, he will choose alternative i if and only if ![]() for all
for all ![]() ,
, ![]() .
.
If we know the utility values ![]() for all
for all ![]() and all
and all ![]() , then it will be very easy for us to calculate which alternative decision‐maker n will choose (and therefore to predict the demand for each alternative). However, since in most cases we do not know the utility values perfectly, we must estimate them. Let
, then it will be very easy for us to calculate which alternative decision‐maker n will choose (and therefore to predict the demand for each alternative). However, since in most cases we do not know the utility values perfectly, we must estimate them. Let ![]() be our estimate of alternative i's utility for decision‐maker n. (The
be our estimate of alternative i's utility for decision‐maker n. (The ![]() values are called representative utilities. We omit a discussion about how these might be calculated; see, for example, Train (2009).) Normally,
values are called representative utilities. We omit a discussion about how these might be calculated; see, for example, Train (2009).) Normally, ![]() , and we use
, and we use ![]() to denote the random estimation error; that is,
to denote the random estimation error; that is,
Choice Probabilities: Once we have determined the ![]() values, we can calculate
values, we can calculate ![]() , the probability that decision‐maker n chooses alternative i, as follows:
, the probability that decision‐maker n chooses alternative i, as follows:
The ![]() values are constants. To estimate the probability, then, we need to know the probability distributions of the random variables
values are constants. To estimate the probability, then, we need to know the probability distributions of the random variables ![]() .
.
Different choice models arise from different distributions of ![]() and different methods for calculating
and different methods for calculating ![]() . For instance, the logit model assumes that
. For instance, the logit model assumes that ![]() are drawn iid from a member of the family of generalized extreme value distributions, and this gives rise to a closed‐form expression for
are drawn iid from a member of the family of generalized extreme value distributions, and this gives rise to a closed‐form expression for ![]() . (Logit is therefore the most widely used discrete choice model.) The probit model, on the other hand, assumes that
. (Logit is therefore the most widely used discrete choice model.) The probit model, on the other hand, assumes that ![]() come from a multivariate normal distribution (and are therefore correlated, not iid), but the resulting
come from a multivariate normal distribution (and are therefore correlated, not iid), but the resulting ![]() values cannot be found in closed form and must instead be estimated using simulation.
values cannot be found in closed form and must instead be estimated using simulation.
2.8.2 The Multinomial Logit Model
Next we derive the multinomial logit model. (Refer to McFadden (1974) or Train (2009) for further details of the derivation.) “Multinomial” means that there are multiple options from which the decision‐maker chooses. (In contrast, binomial models assume there are only two options.) The logit model is obtained by assuming each ![]() is independently and identically distributed from the standard Gumbel distribution, a type of generalized extreme value distribution (also known as type I extreme value). The pdf and cdf of the standard Gumbel distribution are given by
is independently and identically distributed from the standard Gumbel distribution, a type of generalized extreme value distribution (also known as type I extreme value). The pdf and cdf of the standard Gumbel distribution are given by
We can rewrite the probability that decision‐maker n chooses alternative i 2.57 as
Since ![]() has a Gumbel distribution, by 2.59 the probability in the right‐hand side of 2.60 can be written as
has a Gumbel distribution, by 2.59 the probability in the right‐hand side of 2.60 can be written as
if ![]() is given. Since the
is given. Since the ![]() are independent, the cumulative distribution over all
are independent, the cumulative distribution over all ![]() is the product of the individual cumulative distributions:
is the product of the individual cumulative distributions:
Therefore, we can calculate ![]() by conditioning on
by conditioning on ![]() as follows:
as follows:
After some further manipulation (see Problem 2.24), we get
(The sum in the denominator is over all j, including ![]() .) Note that the probability that individual n chooses alternative i is between 0 and 1 (as is necessary for a well defined probability). As
.) Note that the probability that individual n chooses alternative i is between 0 and 1 (as is necessary for a well defined probability). As ![]() , the estimate of i's utility for n, increases, so does the probability that n chooses i; this probability approaches 1 as
, the estimate of i's utility for n, increases, so does the probability that n chooses i; this probability approaches 1 as ![]() approaches
approaches ![]() . Similarly, as
. Similarly, as ![]() decreases, so does the probability that n chooses i, approaching 0 in the limit.
decreases, so does the probability that n chooses i, approaching 0 in the limit.
The expected number of individuals who will choose product i, ![]() , is simply given by
, is simply given by

Of course, we usually don't know ![]() for every individual n, so instead we resort to methods to estimate
for every individual n, so instead we resort to methods to estimate ![]() without relying on too much data. See Koppelman (1975) for a discussion of several useful techniques for this purpose.
without relying on too much data. See Koppelman (1975) for a discussion of several useful techniques for this purpose.
We refer the readers to other texts (Ben‐Akiva and Lerman, 1985; Train, 2009) for details about this and other choice models. We next give an example of how discrete choice modeling techniques can be used to estimate demand in a supply chain management setting.
2.8.3 Example Application to Supply Chain Management
Suppose there is a retailer who sells a set I of products. The retailer wishes to estimate the probability that a given customer would be interested in purchasing product i, for ![]() , so that he can decide which products to offer. Suppose that the customer follows a multinomial logit choice model, as in Section 2.8.2. The retailer's estimate
, so that he can decide which products to offer. Suppose that the customer follows a multinomial logit choice model, as in Section 2.8.2. The retailer's estimate ![]() of the customer's utility
of the customer's utility ![]() for product
for product ![]() is given by
is given by
(Equation 2.64 is identical to 2.56 except that we have dropped the index n since we are considering only a single customer.) If ![]() , then
, then ![]() and
and ![]() denote the actual and estimated utility of making no purchase.
denote the actual and estimated utility of making no purchase.
For any subset ![]() , let
, let ![]() denote the probability that the customer will purchase product i, assuming that her only choices are in the set S, and let
denote the probability that the customer will purchase product i, assuming that her only choices are in the set S, and let ![]() if
if ![]() . Let
. Let ![]() denote the probability that the customer will not purchase any product. Then, from 2.62, we have
denote the probability that the customer will not purchase any product. Then, from 2.62, we have

The retailer's objective is to choose which products to offer in order to maximize his expected profit. Suppose that the retailer earns a profit of ![]() for each unit of product i sold. Suppose also that the retailer cannot offer more than C products. (C might represent shelf space.) Then the retailer needs to solve the following assortment problem:
for each unit of product i sold. Suppose also that the retailer cannot offer more than C products. (C might represent shelf space.) Then the retailer needs to solve the following assortment problem:
(If there are multiple customers, we can just multiply the objective function by the number of customers, assuming they have identical utilities. For a discussion of handling non‐homogenous customers, see Koppelman (1975).) This is a combinatorial optimization problem; the goal is to choose the subset S. This problem is not trivial to solve (though it can be solved efficiently). However, the bigger problem is that the utilities ![]() , and hence the probabilities
, and hence the probabilities ![]() , are unknown to the retailer. One option is for the retailer to offer different assortments of products over time, estimate the utilities based on the observed demands for each assortment, and refine his assortment as his estimates improve. Rusmevichientong et al. (2010) propose such an approach. They introduce a policy that the retailer can follow to generate a sequence of assortments in order to maximize the expected profit over time. The assortment offered in a given period depends on the demands observed in the previous periods. Rusmevichientong et al. (2010) also propose a polynomial‐time algorithm to solve the assortment problem itself.
, are unknown to the retailer. One option is for the retailer to offer different assortments of products over time, estimate the utilities based on the observed demands for each assortment, and refine his assortment as his estimates improve. Rusmevichientong et al. (2010) propose such an approach. They introduce a policy that the retailer can follow to generate a sequence of assortments in order to maximize the expected profit over time. The assortment offered in a given period depends on the demands observed in the previous periods. Rusmevichientong et al. (2010) also propose a polynomial‐time algorithm to solve the assortment problem itself.
PROBLEMS
- 2.1 (Forecasting without Trend) A hospital receives regular shipments of liquefied oxygen, which it converts to oxygen gas that is used for life support. The company that sells the oxygen to the hospital wishes to forecast the amount of liquefied oxygen the hospital will use tomorrow. The number of liters of liquefied oxygen used by the hospital in each of the past 30 days is reported in the file
oxygen.xlsx.- Using a moving average with
 , forecast tomorrow's demand.
, forecast tomorrow's demand. - Using single exponential smoothing with
 , forecast tomorrow's demand.
, forecast tomorrow's demand.
- Using a moving average with
- 2.2 (Forecasting with Trend) The demand for a new brand of dog food has been steadily rising at the local PetMart pet store. The previous 26 weeks' worth of demand (number of bags) are given in the file
dog‐food.xlsx.- Using double exponential smoothing with
 and
and  , forecast next week's demand. Initialize your forecast by setting
, forecast next week's demand. Initialize your forecast by setting  for
for  and
and  .
. - Using linear regression, forecast next week's demand.
- Using double exponential smoothing with
- 2.3 (Forecasting Cupcake Sales) Karl's Cupcakes recently launched a new variety of cupcake. The weekly demands, measured in dozens, during the first two weeks of sales were
 and
and  .
.- Use double exponential smoothing with
 and
and 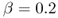 to calculate
to calculate  , the forecast made in week 2 for the demand in week 3.
, the forecast made in week 2 for the demand in week 3. - Suppose the actual demand in week 3 is 59.4. What is
 , the forecast made in week 3 for the demand in week 4?
, the forecast made in week 3 for the demand in week 4?
- Use double exponential smoothing with
- 2.4 (Forecasting with Seasonality) A hardware store sells potting soil, the demand for which is highly seasonal and has also exhibited a slight upward trend. The number of bags of soil sold each month for the past 40 months is reported in the file
potting‐soil.xlsx. Using triple exponential smoothing with ,
,  , and
, and  , forecast the demand for May. Initialize your forecast by setting
, forecast the demand for May. Initialize your forecast by setting 
for periods
 . (There are better ways to initialize this method, but this method is simpler.)
. (There are better ways to initialize this method, but this method is simpler.) - 2.5 (Forecasting Melon Slicers) Matt's Melon Slicers sells specialized knives for watermelons, the demand for which is highly seasonal, with the majority of the demand occurring during the summer. The company has been selling melon slicers for three years and has calculated the following estimates of the seasonal factors, with each period representing one quarter:
Quarter t 
Winter 9 0.4 Spring 10 0.8 Summer 11 1.9 Fall 12 0.9 At the end of period 12, the company calculated the following estimates of the base signal and slope:
 ,
,  .
.- Calculate
 , the forecast made in period 12 for the demand in period 13.
, the forecast made in period 12 for the demand in period 13. - Suppose the demand in period 13 turns out to be 341. Calculate
 ,
,  , and
, and  .
.
- Calculate
- 2.6 (Forecasting Using Regression) The demand for bottled water at football (aka soccer) matches is correlated to the outside temperature at the start of the match. The file
bottled‐water.xlsxreports the temperature (∘C) and number of bottles of water sold for each home match played at a certain stadium for the past two seasons (19 home matches per season).- Using these data, build a linear regression model to relate the demand for bottled water to the match‐time temperature. What are
 and
and  ?
? - The temperatures for the next three matches are predicted to be
 ,
,  , and
, and  , respectively. Forecast the demand for bottled water at each of these matches.
, respectively. Forecast the demand for bottled water at each of these matches.
- Using these data, build a linear regression model to relate the demand for bottled water to the match‐time temperature. What are
- 2.7 (Multiple‐Period‐Ahead Forecasts) In this chapter, we discussed time‐series methods for forecasting the demand one period ahead, i.e., in period
 , we generate a forecast
, we generate a forecast  for the demand in period t. Suppose instead that we wish to forecast multiple periods ahead, i.e., in period
for the demand in period t. Suppose instead that we wish to forecast multiple periods ahead, i.e., in period  , we generate a forecast
, we generate a forecast  for the demand in period
for the demand in period  , for
, for  . Explain how to adapt each of the following methods to handle this case:
. Explain how to adapt each of the following methods to handle this case:- Moving average
- Double exponential smoothing
- Linear regression
- 2.8 (Forecasting using Machine Learning Methods) Using the data set provided in Problem 2.6, choose a learning‐based forecasting method—a tree‐based model, SVR, or neural networks—for forecasting bottled water given temperatures. Use your selected method to forecast the demand during matches when the temperatures are
 ,
,  , and
, and  . Compare your results with those you obtained using linear regression in Problem 2.6(b).
. Compare your results with those you obtained using linear regression in Problem 2.6(b). - 2.9 (Ridge Regression) Ridge regression introduces an
 ‐norm penalty to the objective function of linear regression. Consider a simple version in which we have only a single input (
‐norm penalty to the objective function of linear regression. Consider a simple version in which we have only a single input ( ); then we are minimizing
); then we are minimizing 
where
 is the penalty parameter. Derive closed‐form expressions for
is the penalty parameter. Derive closed‐form expressions for  and
and  . You may use a matrix representation if you wish.
. You may use a matrix representation if you wish. - 2.10 (Forecasting Fires) The file
nyc‐fires.csvcontains the number of fires responded to by the New York City Fire Department on each day from January 1, 2013 through June 30, 2016 (NYC OpenData, 2017). It also contains the high temperature (in ∘F) and the total precipitation (in inches) on the same days (National Oceanic and Atmospheric Administration (NOAA), 2017).Load the data into MATLAB, Excel, or another software package of your choice. Add a variable called
IsWeekendthat indicates whether each day is a weekend day (Saturday or Sunday). Split the data into two parts, one for 2013–2015 (this will be your training data) and one for 2016 (this will be your testing data).In this problem, you will build models to predict the number of fires on a given day using the three features (high temperature, precipitation, and weekend (Y/N)). Use only the training data when building your models.
- Build a linear regression model. Report the coefficients
 .
. - Build a regression tree model with at most 10 branching nodes. (A branching node is a node that has child nodes.) Include a diagram of your tree.
- Build an SVR model. Report the coefficients
 and
and  .
. - For each method in parts (a)–(c), predict the number of fires on each day in the testing data. Report the predicted and actual values and the forecast error for the first 10 records in the testing data. Also report the MSE for each method for the entire testing set.
- Build a linear regression model. Report the coefficients
- 2.11 (Exponential Smoothing for Retail Sales) The file
retail‐sales‐data.csvcontains weekly sales data for 99 departments within 45 retail stores over approximately 3 years. This is actual data from a real company but has been anonymized (see Kaggle.com (2017)).- Extract the sales data for store 2, department 93. Determine the most appropriate form of exponential smoothing (single, double, or triple) and apply that method to forecast the sales. Use 0.15 for all of the smoothing constants (
 ,
,  , and/or
, and/or  ). Begin forecasting at the earliest period you can. (For example, in double exponential smoothing the forecasts begin in period 3.) Report the MSE, MAD, and MAPE for your forecasts. Plot the actual and forecast sales on a single plot.
). Begin forecasting at the earliest period you can. (For example, in double exponential smoothing the forecasts begin in period 3.) Report the MSE, MAD, and MAPE for your forecasts. Plot the actual and forecast sales on a single plot. - Repeat part (a) for store 3, department 60.
- Repeat part (a) for store 1, department 16.
- Extract the sales data for store 2, department 93. Determine the most appropriate form of exponential smoothing (single, double, or triple) and apply that method to forecast the sales. Use 0.15 for all of the smoothing constants (
- 2.12 (Mean and Variance of Exponential Smoothing Forecast Error) Prove 2.31equations and 2.32.
- 2.13 (Forecasting Simulation) Consider a product whose daily demand follows 2.30 with
 and
and  .
.- Build a spreadsheet simulation of the demand process, as well as a moving average forecast of order 5. Simulate the system for at least 500 periods. Report the MSE and MAD of the forecast. Also calculate the standard deviation of the forecast error. How accurate is the approximation given in 2.28 for your simulated values?
- Repeat part (a) for an exponential smoothing forecast with constant
 .
. - Based on the results of parts (a) and (b), does one forecasting method appear to work better than the other?
- 2.14 (Bass Diffusion for LPhone) HCT, an Asian manufacturer of a new 4G cell phone, the LPhone 5, is planing to enter the U.S. market, and they are in the process of signing a contract with a third‐party logistics (3PL) provider in which they must specify the size of the warehouse they want to rent from the 3PL. HCT wants to forecast the total sales of the LPhone 5, as well as the time at which the LPhone 5 reaches its peak sales. After some thorough market research, HCT has estimated that
 ,
,  , and
, and  million. Calculate when the peak sales will occur and how many LPhone 5 the company will have sold by that point.
million. Calculate when the peak sales will occur and how many LPhone 5 the company will have sold by that point. - 2.15 (Bass Diffusion for iPeel) Banana Computer Co. plans to launch its latest consumer electronic device, the iPeel, early next year. Based on market research, it estimates that the market potential for the iPeel is 170,000 units, with coefficients of innovation and imitation of 0.07 and 0.31, respectively.
- If the iPeel is introduced on January 1, on what date will the sales peak? What will be the demand rate on that date, and how many units will have been sold?
- On what date will 90% of the sales have occurred?
- Plot the demand rate and cumulative demand as a function of time.
- 2.16 (Bass Diffusion for Books) A new novel was published recently, and the demand for it is expected to follow a Bass diffusion process. The publisher decided to print only a limited number of copies, observe the demand for the book for 20 weeks, estimate the Bass parameters, and then undertake a second printing for the remainder of the life cycle of the book using these parameters. The demand for the book during these 20 weeks is reported in the file
novel.xlsx. Using these data, estimate m, p, and q using the method described in Section 2.6.3. - 2.17 (Proof of Corollary 2.1) Prove Corollary 2.1.
- 2.18 (Influentials and Imitators) Suppose that potential adopters of a given product fall into two distinct segments: influentials and imitators. Each segment has its own within‐segment innovation and imitation parameters and experiences its own Bass‐type contagion process. In addition, the influentials can exert a cross‐segment influence on the imitators, but not vice‐versa. Let
 denote the proportion of influentials in the population of eventual adopters (
denote the proportion of influentials in the population of eventual adopters ( ), and
), and  denote the proportion of imitators. Let
denote the proportion of imitators. Let  and
and  denote the within‐segment innovation and imitation parameters, respectively, for
denote the within‐segment innovation and imitation parameters, respectively, for  , where
, where  represents influentials and
represents influentials and  represents imitators. Let
represents imitators. Let  denote the cross‐segment imitation parameter.
denote the cross‐segment imitation parameter.
- 2.19 (Demand Diffusion across Multiple Markets) A company plans to introduce a variety of new products to multiple vertical markets. The demands from these verticals are likely to follow different diffusion patterns. The company is interested in combining diffusion models derived from different vertical markets to help characterize the overall market demand. However, they are not sure about whether doing so would introduce additional variances and biases into the forecast. Show that combining forecasts of different diffusion models using weights that are inversely proportional to their forecast variances yields a combined forecast variance that is smaller than the forecast variance of each individual diffusion model.
- 2.20 (Leading Indicators) A battery manufacturer produces a large number of models of lithium‐ion batteries for use in computers and other electronic devices. The products are introduced at different times and follow different demand processes. The company wishes to determine whether some of the products can serve as leading indicators for the rest of the products. The file
batteries.xlsxcontains historical demand data for 25 products for the past 26 weeks.- Using Algorithm 2.1 with parameters
 ,
,  , and
, and  , determine all pairs
, determine all pairs  such that product i is a leading indicator with lag k. (Note: You should not need to recluster the products.)
such that product i is a leading indicator with lag k. (Note: You should not need to recluster the products.) - Using one of the
 you found in part (a), forecast the demand for the rest of the cluster in periods 27 and 28.
you found in part (a), forecast the demand for the rest of the cluster in periods 27 and 28.
- Using Algorithm 2.1 with parameters
- 2.21 (Discrete Choice with Uniform Errors) Suppose that, in the discrete choice model, the estimation error
 has a
has a  distribution for all n and i. Write an expression for
distribution for all n and i. Write an expression for  , analogous to 2.61. Your expression may include
, analogous to 2.61. Your expression may include 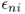 ,
, 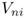 , and
, and  , but not
, but not  .
. - 2.22 (Discrete Choices for Day Care) A university is in the process of choosing a location for a new day care center for its faculty's children. The two options for the location are city A, where the university is located, or city B, a neighboring city known for larger houses but a longer commute. The university wants to estimate the number of faculty with kids who are living or will live in city A during the next 10 years. To that end, the university wishes to estimate the choice probability between the two cities for a typical family. Suppose that the utility a family obtains from living in each city depends only on the average house purchase price, the distance between the city and the campus, and the family's opinion of the convenience and quality of life of each city. The first two of these factors can be observed by the researcher, but the researcher cannot observe the third. The researcher believes that the observed part of the utility is a linear function of the observed factors; in particular, the utility of living in each city can be written as

where the subscripts A and B denote city A and city B, and
 and D are the purchase price and distance. The unobserved component of the utility for each alternative,
and D are the purchase price and distance. The unobserved component of the utility for each alternative,  and
and  , vary across households depending on how each household views the quality and convenience of living in each city. If these unobserved components are distributed iid with a standard Gumbel distribution, calculate the probability that a household will choose to live in city A.
, vary across households depending on how each household views the quality and convenience of living in each city. If these unobserved components are distributed iid with a standard Gumbel distribution, calculate the probability that a household will choose to live in city A. - 2.23 (Using Discrete Choice to Forecast Movie Sales) Three new movies will be shown at a movie theater this weekend. The theater wishes to estimate the expected number of people who will come to see each movie so they can decide how many screenings to offer, how large a theater each movie should be shown in, and so on. The movie studios that produced the three movies held “sneak peak” screenings of the films and conducted post‐movie interviews of the attendees. Based on these interviews, they estimated the utility of each movie based on a viewer's age range. They also estimated the utility of not seeing any movie. These estimated utilities are denoted
 , although here n refers not to an individual but to a type of individual (based on age range). The following table lists the
, although here n refers not to an individual but to a type of individual (based on age range). The following table lists the  values, as well as the number of people who are considering seeing a movie at that theater this weekend.
values, as well as the number of people who are considering seeing a movie at that theater this weekend. Age Range Movie 16–25 26–35 36+ Prognosis Negative 0.22 0.54 0.62 Rochelle, Rochelle 0.49 0.57 0.51 Sack Lunch 0.53 0.31 0.38 No movie 0.10 0.27 0.41 Population 700 1900 1150 - Assume that the actual utilities
 differ from the estimated utilities
differ from the estimated utilities  by an additive iid error term that has a standard Gumbel distribution. Using the multinomial logit model of Section 2.8.2, calculate the expected demand for each movie.
by an additive iid error term that has a standard Gumbel distribution. Using the multinomial logit model of Section 2.8.2, calculate the expected demand for each movie. - Now suppose the movie theater doesn't know about the multinomial logit model and assumes that
 is simply calculated using a weighted sum of the
is simply calculated using a weighted sum of the  values; that is,
values; that is, 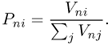
What are the expected demands for each movie using this method?
- Assume that the actual utilities
- 2.24 (Proof of 2.62) Prove 2.62equation .



