9.2 The EM algorithm

9.2.1 The idea of the EM algorithm

A useful numerical technique which finds the posterior mode, that is, the value at which or equivalently is a maximum, but does not provide full information on the posterior distribution is the EM algorithm. We can exemplify this by an example on genetic linkage due to Rao (1973, Section 5g) quoted by Dempster et al. (1977), by Gelfand and Smith (1990) and by Tanner (1996, Section 4.1). We have observations with cell probabilities

and we want to estimate η. The likelihood is then

What we do is to augment the data by adding further data to produce augmented data . It should be noted that to a considerable extent the distinction between parameters of a model and augmentations to the data is artificial (i.e. fictitious augmentations to the data can be regarded as parameters of a model). In the example under consideration, the augmentation consists simply in splitting the first cell into two cells with probabilities and . The advantage of this is that the likelihood then takes the much simpler form

and if we take the standard reference prior Be(0, 0), then the posterior is a beta distribution

Not much in life is free, and in this case we have to pay for the greater simplicity of the model by estimating the split of x1 into y0 and y1. The EM algorithm for finding the posterior mode is an iterative method starting from some plausible guess for the value of η. At stage t, we suppose that the current guess is . Each stage has two steps. In the first, the E-step (expectation step), we compute

that is, the expectation of the log-likelihood function, the expectation being computed at , so that

In the second step, the M-step (the maximization step), we we find that value of η which maximizes . In this particular example as yi=xi for i> 1

For the M-step, we note that

and equating this to zero we deduce that

Since y1 has a binomial distribution with

so that

the iteration becomes

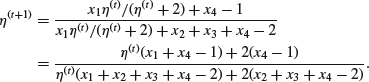
The values actually observed were x1=125, x2=18, x3=20, x4=34. We can then estimate η by iteration starting from, for example, and using

In fact, the iteration will converge to the positive root of which is 0.630.

9.2.2 Why the EM algorithm works

We will first show that increases with t and, presuming that converges to some limit , then show that at so that will normally be the posterior mode.

From the obvious equation considered conditional on , it follows, on noting that includes and hence , that

Multiplying both sides by the density and integrating (noting that the left hand side does not depend on ), we get for any fixed

(we note that K clearly does not depend on η). Taking , we get

Now because of the way in which we chose . Moreover,

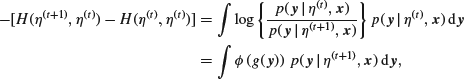
where

Because (as is easily seen by differentiation) takes a minimum value of 0 when u=1, we see that for all t. Consequently,

so that

We now show that the limit is a stationary point. As

we see that provided Q is a reasonably smooth function

Further

and in particular taking

Since for any fixed , and in particular for , it now follows that

so that is a stationary point, which will usually be the posterior mode.

More information about the EM algorithm can be found in Dempster et al. (1977) or Tanner (1996).

9.2.3 Semi-conjugate prior with a normal likelihood

Suppose that we have independent normally distributed observations x1, x2, … , . We use the notation

In Section 2.13, we noted that the conjugate joint prior for the normal mean and variance is not a product of a function of θ and , so that θ and are not independent a priori. Nevertheless, an assumption of prior independence would seem appropriate for many problems, and so we are sometimes led to consider a situation in which

independently of one another. Such a prior is described as semi-conjugate by Gelman et al. (2004, Section 3.4) and as conditionally conjugate by O’Hagan (2004, Section 6.33). The latter term arises because conditional on knowledge of θ, it is a conjugate prior for and vice versa.

With such a prior, we know that, conditional on knowledge of , the posterior of θ is

where

(cf. Section 2.3) whereas, conditional on knowledge of θ, the posterior of is

where

(cf. Section 2.7).

In such a case, we can use the EM algorithm to estimate the posterior mode of θ, effectively augmenting the data with the variance . We begin by observing that (ignoring terms which do not depend on θ) the log posterior density is

To carry out the E-step we first note that since

and the expectation of a chi-squared variate is equal to its number of degrees of freedom, we know that

where and . For the M-step we must find that value which maximizes . But is of the form of the log of the posterior density we would have got for θ had we had the same prior () and observations with mean θ and known variance S1/n1. Now it follows from Section 2.3 on ‘Several normal observations with a normal prior’ that the posterior mean of θ in this case is at

(the right-hand side depends on through S1), and so we see that this is the value of θ giving the required maximum.

To illustrate this case, we return to the data on wheat yield considered in the example towards the end of Section 2.13 in which n=12, and S=13 045. We will take the prior for the variance considered in that Section, namely, with S0=2700 and . For the mean, we will take a prior which is where and , which approximates well to the values for the marginal distribution in that Section (according to which ). The resulting marginal densities are nearly the same, but because we now assume prior independence the joint distribution is different.

It seems that a reasonable starting point for the iteration is . Then we get , , and thereafter.

9.2.4 The EM algorithm for the hierarchical normal model

The EM algorithm is well suited to the analysis of hierarchical models and we can see this by examining the important case of the hierarchical normal model. Although the formulae we shall derive do not look pretty, they are very easy to use. Suppose that

with , where

as in Section 8.5 and that we wish to estimate the hyperparameters μ, and . In this case takes the place of η in the example on genetic linkage, while we augment the data by to give augmented data . We can use a reference prior for , but (as mentioned in Section 8.5) this will not work for . Accordingly, we will adopt the prior

It is then easily seen that (up to an additive constant)

To carry out the E-step, observe that conditional on the value of the parameters where

using the notation introduced in Section 6.5 for averaging over a suffix (cf. Section 2.3). We can now see that

and similarly

so that

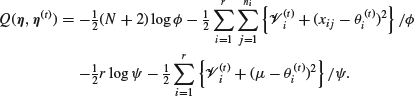
It is now clear that the M-step gives

9.2.5 A particular case of the hierarchical normal model

Gelman et al. (2004, Table 11.2) quote the following data from Box et al. (1978, Table 6.1) on the coagulation time in seconds for blood drawn from N=24 animals randomly allocated to four different diets:

The data has been slightly adjusted, so that the averages come out to be whole numbers. It should perhaps be noted that the prior adopted in this and the preceding subsections differs slightly from that adopted by Gelman et al. The within-groups sum of squares is and the overall mean is . It, therefore, seems reasonable to start iterations from and . As for , we can take

This results in

Similarly, we get , , , , and .

We can now feed these values in and commence the iteration, getting , and . Continuing the iteration, we get rapid convergence to , , , , , and .