7.9 Exercises on Chapter 7
1. Show that in any experiment E in which there is a possible value y for the random variable  such that
such that  , then if z is any other possible value of
, then if z is any other possible value of  , the statistic t=t(x) defined by
, the statistic t=t(x) defined by

is sufficient for θ given x. Hence, show that if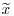 is a continuous random variable, then a naïve application of the weak sufficiency principle as defined in Section 7.1 would result in
is a continuous random variable, then a naïve application of the weak sufficiency principle as defined in Section 7.1 would result in 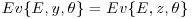 for any two possible values y and z of
for any two possible values y and z of  .
.
is sufficient for θ given x. Hence, show that if
2. Consider an experiment  . We say that censoring (strictly speaking, fixed censoring) occurs with censoring mechanism g (a known function of x) when, instead of
. We say that censoring (strictly speaking, fixed censoring) occurs with censoring mechanism g (a known function of x) when, instead of  , one observes y=g(x). A typical example occurs when we report x if x< k for some fixed k, but otherwise simply report that
, one observes y=g(x). A typical example occurs when we report x if x< k for some fixed k, but otherwise simply report that  . As a result, the experiment really performed is
. As a result, the experiment really performed is 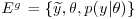 . A second method with censoring mechanism h is said to be equivalent to the first when
. A second method with censoring mechanism h is said to be equivalent to the first when

As a special case, if g is one-to-one then the mechanism is said to be equivalent to no censoring. Show that if two censoring mechanisms are equivalent, then the likelihood principle implies that

As a special case, if g is one-to-one then the mechanism is said to be equivalent to no censoring. Show that if two censoring mechanisms are equivalent, then the likelihood principle implies that
3. Suppose that the density function 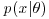 is defined as follows for
is defined as follows for  and
and 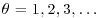 . If θ is even, then
. If θ is even, then

if θ is odd but θ ≠ 1, then

while if θ = 1 then
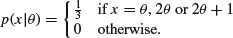
Show that, for any x the data intuitively give equal support to the three possible values of θ compatible with that observation, and hence that on likelihood grounds any of the three would be a suitable estimate. Consider, therefore, the three possible estimators d1, d2 and d3 corresponding to the smallest, middle and largest possible θ. Show that
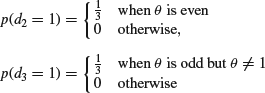
but that
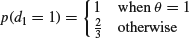
Does this apparent discrepancy cause any problems for a Bayesian analysis (due to G. Monette and D. A. S. Fraser)?
if θ is odd but θ ≠ 1, then
while if θ = 1 then
Show that, for any x the data intuitively give equal support to the three possible values of θ compatible with that observation, and hence that on likelihood grounds any of the three would be a suitable estimate. Consider, therefore, the three possible estimators d1, d2 and d3 corresponding to the smallest, middle and largest possible θ. Show that
but that
Does this apparent discrepancy cause any problems for a Bayesian analysis (due to G. Monette and D. A. S. Fraser)?
4. A drunken soldier, starting at an intersection O in a city which has square blocks, staggers around a random path trailing a taut string. Eventually, he stops at an intersection (after walking at least one block) and buries a treasure. Let θ denote the path of the string from O to the treasure. Letting N, S, E and W stand for a path segment one block long in the indicated direction, so that θ can be expressed as a sequence of such letters, say  . (Note that NS, SN, EW and WE cannot appear as the taut string would be rewound). After burying the treasure, the soldier walks one block further in a random direction (still keeping the string taut). Let X denote this augmented path, so that X is one of θN, θS, θE and θW, each with probability
. (Note that NS, SN, EW and WE cannot appear as the taut string would be rewound). After burying the treasure, the soldier walks one block further in a random direction (still keeping the string taut). Let X denote this augmented path, so that X is one of θN, θS, θE and θW, each with probability  . You observe X and are then to find the treasure. Show that if you use a reference prior
. You observe X and are then to find the treasure. Show that if you use a reference prior  for all possible paths θ, then all four possible values of θ given X are equally likely. Note, however, that intuition would suggest that θ is three times as likely to extend the path as to backtrack, suggesting that one particular value of θ is more likely than the others after X is observed (due to M. Stone).
for all possible paths θ, then all four possible values of θ given X are equally likely. Note, however, that intuition would suggest that θ is three times as likely to extend the path as to backtrack, suggesting that one particular value of θ is more likely than the others after X is observed (due to M. Stone).
5. Suppose that, starting with a fortune of units, you bet units each time on evens at roulette (so that you have a probability of 18/37 of winning at Monte Carlo or 18/38 at Las Vegas) and keep a record of your fortune and the difference between the number of times you win and the number of times you lose in games. Which of the following are stopping rules?
a. The last time n at which  .
.
b. The first time that you win in three successive games.
c. The value of n for which  .
.
6. Suppose that is a sequential sample from an distribution and it is desired to test versus . The experimenter reports that he used a proper stopping rule and obtained the data 3, , 2, 1.
a. What could a frequentist conclude?
b. What could a Bayesian conclude?
7. Let  be a sequential sample from a Poisson distribution
be a sequential sample from a Poisson distribution  ). Suppose that the stopping rule is to stop sampling at time
). Suppose that the stopping rule is to stop sampling at time  with probability
with probability
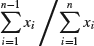
for (define 0/0=1). Suppose that the first five observations are 3, 1, 2, 5, 7 and that sampling then stops. Find the likelihood function for λ (Berger, 1985).
(define 0/0=1). Suppose that the first five observations are 3, 1, 2, 5, 7 and that sampling then stops. Find the likelihood function for λ (Berger, 1985).
for
8. Show that the mean of the beta-Pascal distribution

is given by the formula in Section 7.3, namely,

is given by the formula in Section 7.3, namely,
9. Suppose that you intend to observe the number x of successes in n Bernoulli trials and the number y of failures before the nth success after the first n trials, so that 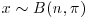 and
and 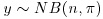 . Find the likelihood function
. Find the likelihood function 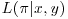 and deduce the reference prior that Jeffreys’ rule would suggest for this case.
and deduce the reference prior that Jeffreys’ rule would suggest for this case.
10. The negative of loss is sometimes referred to as utility. Consider a gambling game very unlike most in that you are bound to win at least £2, and accordingly in order to be allowed to play, you must pay an entry fee of £e. A coin is tossed until it comes up heads, and if this occurs for the first time on the nth toss, you receive £2n. Assuming that the utility to you of making a gain of £x is u(x), find the expected utility of this game, and then discuss whether it is plausible that u(x) is directly proportional to x. [The gamble discussed here is known as the St Petersburg Paradox. A fuller discussion of it can be found in Leonard and Hsu (2001, Chapter 4).]
11. Suppose that you want to estimate the parameter  of a binomial distribution
of a binomial distribution 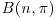 . Show that if the loss function is
. Show that if the loss function is
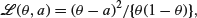
then the Bayes rule corresponding to a uniform [i.e.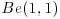 ] prior for
] prior for 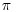 is given by d(x)=x/n for any x such that 0< x< n, that is, the maximum likelihood estimator. Is d(x)=x/n a Bayes rule if x = 0 or x=n?
is given by d(x)=x/n for any x such that 0< x< n, that is, the maximum likelihood estimator. Is d(x)=x/n a Bayes rule if x = 0 or x=n?
then the Bayes rule corresponding to a uniform [i.e.
12. Let  and
and 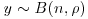 have independent binomial distributions of the same index but possibly different parameters. Find the Bayes rule corresponding to the loss
have independent binomial distributions of the same index but possibly different parameters. Find the Bayes rule corresponding to the loss
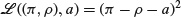
when the priors for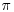 and ρ are independent uniform distributions.
and ρ are independent uniform distributions.
when the priors for
13. Investigate possible point estimators for  on the basis of the posterior distribution in the example in the subsection of Section 2.10 headed ‘Mixtures of conjugate densities’.
on the basis of the posterior distribution in the example in the subsection of Section 2.10 headed ‘Mixtures of conjugate densities’.
14. Find the Bayes rule corresponding to the loss function

15. Suppose that your prior for the proportion of defective items supplied by a manufacturer is given by the beta distribution , and that you then observe that none of a random sample of size 6 is defective. Find the posterior distribution and use it to carry out a test of the hypothesis using
a. a ‘0 – 1’ loss function, and
b. the loss function


16. Suppose there is a loss function 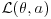 defined by
defined by

On the basis of an observation x you have to take action a0, a1 or a2. For what values of the posterior probabilities p0 and p1 of the hypotheses and
and  would you take each of the possible actions?
would you take each of the possible actions?

On the basis of an observation x you have to take action a0, a1 or a2. For what values of the posterior probabilities p0 and p1 of the hypotheses
17. A child is given an intelligence test. We assume that the test result is where is the true intelligence quotient of the child, as measured by the test (in other words, if the child took a large number of similar tests, the average score would be ). Assume also that, in the population as a whole, is distributed according to an distribution. If it is desired, on the basis of the intelligence quotient, to decide whether to put the child into a slow, average or fast group for reading, the actions available are:
a. a1: Put in slow group, that is, decide 
b. a1: Put in average group, that is, decide 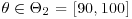
c. a1: Put in fast group, that is, decide 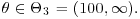
A loss function of the following form might be deemed appropriate:

Assume that you observe that the test result = 115. By using tables of the normal distribution and the fact that if is the density function of the standard normal distribution, then , find is the appropriate action to take on the basis of this observation. [See Berger (1985, Sections 4.2–4.4)].

Assume that you observe that the test result = 115. By using tables of the normal distribution and the fact that if is the density function of the standard normal distribution, then , find is the appropriate action to take on the basis of this observation. [See Berger (1985, Sections 4.2–4.4)].
18. In Section 7.8, a point estimator  for the current value λ of the parameter of a Poisson distribution was found. Adapt the argument to deal with the case where the underlying distribution is geometric, that is
for the current value λ of the parameter of a Poisson distribution was found. Adapt the argument to deal with the case where the underlying distribution is geometric, that is
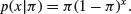
Generalize to the case of a negative binomial distribution, that is,
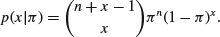
Generalize to the case of a negative binomial distribution, that is,
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
