7.5 Bayesian decision theory

7.5.1 The elements of game theory

Only a very brief account of this important topic is included here; readers who want to know more should begin by consulting Berger (1985) and Ferguson (1967).

The elements of decision theory are very similar to those of the mathematical theory of games as developed by von Neumann and Morgenstern (1953), although for statistical purposes one of the players is nature (in some sense) rather than another player. Only those aspects of the theory of games which are strictly necessary are given here; an entertaining popular account is given by Williams (1966). A two-person zero-sum game has the following three basic elements:

1. A non-empty set θ of possible states of nature θ, sometimes called the parameter space;

2. A non-empty set A of actions available to the statistician;

3. A loss function L, which defines the loss which a statistician suffers if he takes action a when the true state of nature is θ (this loss being expressed as a real number).

A statistical decision problem or a statistical game is a game coupled with an experiment whose result x lies in a sample space and is randomly distributed with a density which depends on the state ‘chosen’ by nature. The data x can be, and usually is, more than one-dimensional.

Now suppose that on the basis of the result x of the experiment, the statistician chooses an action , resulting in a random loss . Taking expectations over possible outcomes x of the experiment, we get a risk function

which depends on the true state of nature and the form of the function d by which the action to be taken once the result of the experiment is known is determined. It is possible that this expectation may not exist, or may be infinite, but we shall exclude such cases and define a (nonrandomized) decision rule or a decision function as any function d for which exists and is finite for all .

An important particular case of an action dependent on the outcome of an experiment is that of a point estimators of a parameter θ, that is, to find a single number from the data which in some way best represents a parameter under study.

For classical statisticians, an important notion is admissibility. An estimator is said to dominate an estimator if

for all θ with strict inequality for at least one value of θ. An estimator is said to be inadmissible if it is dominated by some other action . The notion of admissibility is clearly related to that of Pareto optimality. [‘Pareto optimality’ is a condition where no one is worse off in one state than another but someone is better off, and there is no state ‘Pareto superior’ to it (i.e. in which more people would be better off without anyone being worse off).]

From the point of view of classical statisticians, it is very undesirable to use inadmissible actions. From a Bayesian point of view, admissibility is not generally very relevant. In the words of Press (1989, Section 2.3.1),

Admissibility requires that we average over all possible values of the observable random variables (the expectation is taken with respect to the observables). In experimental design situations, statisticians must be concerned with the performance of estimators for many possible situational repetitions and for many values of the observables, and then admissibility is a reasonable Bayesian performance criterion. In most other situations, however, statisticians are less concerned with performance of an estimator over many possible samples that have yet to be observed than they are with the performance of their estimator conditional upon having observed this particular data set conditional upon having observed this particular data set and conditional upon all prior information available. For this reason, in non-experimental design situations, admissibility is generally not a compelling criterion for influencing our choice of estimator.

For the moment we shall, however, follow the investigation from a classical standpoint.

From a Bayesian viewpoint, we must suppose that we have prior beliefs about θ which can be expressed in terms of a prior density . The Bayes risk r(d) of the decision rule d can then be defined as the expectation of over all possible values of θ, that is,

It seems sensible to minimize one’s losses, and accordingly a Bayes decision rule d is defined as one which minimizes the Bayes risk r(d). Now

It follows that if the posterior expected loss of an action a is defined by

then the Bayes risk is minimized if the decision rule d is so chosen that is a minimum for all x (technically, for those who know measure theory, it need only be a minimum for almost all x).

Raiffa and Schlaifer (1961, Sections 1.2–1.3) refer to the overall minimization of r(d) as the normal form of Bayesian analysis and to the minimization of for all x as the extensive form; the aforementioned remark shows that the two are equivalent.

When a number of possible prior distributions are under consideration, one sometimes finds that the term Bayes rule as such is restricted to rules restricting from proper priors, while those resulting from improper priors are called generalized Bayes rules. Further extensions are mentioned in Ferguson (1967).

7.5.2 Point estimators resulting from quadratic loss

A Bayes decision rule in the case of point estimation is referred to as a Bayes estimator. In such problems, it is easiest to work with quadratic loss, that is, with a squared-error loss function

In this case, is the mean square error, that is,

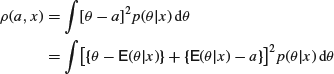
The second term clearly vanishes, so that

which is a minimum when , so that a Bayes estimator d(x) is the posterior mean of θ, and in this case is the posterior variance of θ.

7.5.3 Particular cases of quadratic loss

As a particular case, if we have a single observation where is known and our prior for θ is , so that our posterior is (cf. Section 2.2 on ‘Normal prior and likelihood’), then an estimate of θ that minimizes quadratic loss is the posterior mean , and if that estimate is used the mean square error is the posterior variance .

For another example, suppose that , that is, that x has a Poisson distribution of mean λ, and that our prior density for λ is . First note that the predictive density of x is

To avoid ambiguity in what follows, is used for this predictive distribution, so that just denotes . Then as

it follows that the posterior mean is

We shall return to this example in Section 7.8 in connection with empirical Bayes methods.

Note incidentally that if the prior is , then the posterior is (as shown in Section 3.4 on ‘The Poisson distribution’), so that in this particular case

7.5.4 Weighted quadratic loss

However, you should not go away with the conclusion that the solution to all problems of point estimation from a Bayesian point of view is simply to quote the posterior mean – the answer depends on the loss function. Thus, if we take as loss function a weighted quadratic loss, that is,

then

If we now define

then similar calculations to those above show that

and hence that a Bayes decision results if

that is, d(x) is a weighted posterior mean of θ.

7.5.5 Absolute error loss

A further answer results if we take as loss function the absolute error

in which case

is sometimes referred to as the mean absolute deviation or MAD. In this case, any median m(x) of the posterior distribution given x, that is, any value such that

is a Bayes rule. To show this suppose that d(x) is any other rule and, for definiteness, that d(x)> m(x) for some particular x (the proof is similar if d(x)< m(x)). Then

while for

so that

and hence on taking expectations over θ

from which it follows that taking the posterior median is indeed the appropriate Bayes rule for this loss function. More generally, a loss function which is if but if results in a Bayes estimator which is a v/(u+v) fractile of the posterior distribution.

7.5.6 Zero-one loss

Yet another answer results from the loss function

which results in

Consequently, if a modal interval of length is defined as an interval

which has highest probability for given , then the midpoint of this interval is a Bayes estimate for this loss function. [A modal interval is, of course, just another name for a highest density region (HDR) except for the presumption that will usually be small.] If is fairly small, this value is clearly very close to the posterior mode of the distribution, which in its turn will be close to the maximum likelihood estimator if the prior is reasonably smooth.

Thus all three of mean, median and mode of the posterior distribution can arise as Bayes estimators for suitable loss functions (namely, quadratic error, absolute error and zero-one error, respectively).

7.5.7 General discussion of point estimation

Some Bayesian statisticians pour scorn on the whole idea of point estimators; see Box and Tiao (1992 Section A5.6). There are certainly doubtful points about the preceding analysis. It is difficult to be convinced in any particular case that a particular loss function represents real economic penalties in a particular case, and in many scientific contexts, it is difficult to give any meaning at all to the notion of the loss suffered by making a wrong point estimate. Certainly, the same loss function will not be valid in all cases. Moreover, even with quadratic loss, which is often treated as a norm, there are problems which do not admit of an easy solution. If, for example, , then it would seem reasonable to estimate θ by , and yet the mean square error is infinite. Of course, such decision functions are excluded by requiring that the risk function should be finite, but this is clearly a case of what Good (1965, Section 6.2) referred to as ‘adhockery’.

Even though there are cases (e.g. where the posterior distribution is bimodal) in which there is no sensible point estimator, I think there are cases where it is reasonable to ask for such a thing, though I have considerable doubts as to whether the ideas of decision theory add much to the appeal that quantities such as the posterior mean, median or mode have in themselves.