6.7 The general linear model

6.7.1 Formulation of the general linear model

All of the last few sections have been concerned with particular cases of the so-called general linear model. It is possible to treat them all at once in an approach using matrix theory. In most of this book, substantial use of matrix theory has been avoided, but if the reader has some knowledge of matrices this section may be helpful, in that the intention here is to put some of the models already considered into the form of the general linear model. An understanding of how these models can be put into such a framework, will put the reader in a good position to approach the theory in its full generality, as it is dealt with in such works as Box and Tiao (1992).

It is important to distinguish row vectors from column vectors. We write for a column vector and for its transpose; similarly if is an matrix then is its transpose. Consider a situation in which we have a column vector of observations, so that (the equation is written thus to save the excessive space taken up by column vectors). We suppose that the xi are independently normally distributed with common variance and a vector of means satisfying

where is a vector of unknown parameters and is a known matrix.

In the case of the original formulation of the bivariate linear regression model in which, conditional on xi, we have then takes the part of , r = 2, takes the part of and takes the part of where

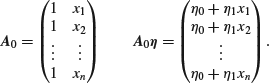
This model is reformulated in terms of and

In the case of the one way model (where, for simplicity, we shall restrict ourselves to the case where Ki=K for all i), and

The two way layout can be expressed similarly using a matrix of 0s and 1s. It is also possible to write the multiple regression model

(the xij being treated as known) as a case of the general linear model.

6.7.2 Derivation of the posterior

Noting that for any vector we have , we can write the likelihood function for the general linear model in the form

Taking standard reference priors, that is, the posterior is

Now as and scalars equal their own transposes

so that if is such that

(so that ), that is, assuming is non-singular,

we have

where

It is also useful to define

Because is of the form , it is always non-negative, and it clearly vanishes if . Further, Se is the minimum value of the sum of squares S and so is positive. It is sometimes worth noting that

as is easily shown.

It follows that the posterior can be written as

In fact, this means that for given the vector has a multivariate normal distribution of mean and variance–covariance matrix .

If you are now interested in as a whole you can now integrate with respect to to get

where

It may also be noted that the set

is a hyperellipsoid in r-dimensional space in which the length of each of the axes is in a constant ratio to . The argument of Section 6.5 on the one way layout can now be adapted to show that , so that E(F) is an HDR for of probability p if F is the appropriate percentage point of .

6.7.3 Inference for a subset of the parameters

However, it is often the case that most of the interest centres on a subset of the parameters, say on . If so, then it is convenient to write and . If it happens that splits into a sum

then it is easy to integrate

to get

and thus as

where

It is now easy to show that and hence to make inferences for .

Unfortunately, the quadratic form does in general contain terms where but j> k and hence it does not in general split into . We will not discuss such cases further; useful references are Box and Tiao (1992), Lindley and Smith (1972) and Seber (2003).

6.7.4 Application to bivariate linear regression

The theory can be illustrated by considering the simple linear regression model. Consider first the reformulated version in terms of and . In this case

and the fact that this matrix is easy to invert is one of the underlying reasons why this reformulation was sensible. Also

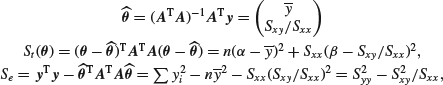
so that Se is what was denoted See in Section 6.3 on bivariate linear regression.

If you are particularly interested in α, then in this case the thing to do is to note that the quadratic form splits with and . Consequently, the posterior distribution of is given by

Since the square of a tn–2 variable can easily be shown to have an F1,n–2 distribution, this conclusion is equivalent to that of Section 6.3.

The greater difficulties that arise when is non-diagonal can be seen by following the same process through for the original formulation of the bivariate linear regression model in terms of and . In this case it is easy enough to find the posterior distribution of , but it involves some rearrangement to get that of .