6.5 Comparison of several means – the one way model

6.5.1 Description of the one way layout

Sometimes we want to compare more than two samples. We might, for example, wish to compare the performance of children from a number of schools at a standard test. The usual model for such a situation is as follows. We suppose that is a vector of unknown parameters and that there are independent observations

from I independent populations with, however, a common variance . For simplicity, we shall assume independent reference priors uniform in and , that is

The likelihood is

where

and so the posterior is

It is useful to define the following notation

The reason for thinking of the is that we are often concerned as to whether all the are equal. If, for example, the xik represent yields of wheat on fields on which I different fertilizers have been used, then we are likely to be interested in whether the yields are on average all equal (or nearly so), that is, or equivalently whether or not

The satisfy the condition

so that if we know the values of we automatically know

Similarly the satisfy .

6.5.2 Integration over the nuisance parameters

Since the Jacobian determinant of the transformation which takes , to consists of entries all of which are 1/n, 1 or 0, its value is a constant, and so

The thing to do now is to re-express S in terms of . Since and it follows that

It is easily checked that sums of products of terms on the right vanish, and so it easily follows that

where

It is also useful to define

It follows that the posterior may be written in the form

As explained earlier, the value of λ is not usually of any great interest, and it is easily integrated out to give

The variance can now be integrated out in just the same way as it was in Section 2.12 on ‘Normal mean and variance both unknown’ by reducing to a standard gamma function integral. The result is that

where

This is similar to a result obtained in one dimension (see Section 2.12 again; the situation there is not quite that we get by setting I = 1 here because here λ has been integrated out). In that case we deduced that

where

By analogy with that situation, the posterior distribution for is called the multivariate t distribution. It was discovered independently by Cornish (1954 and 1955) and by Dunnett and Sobel (1954). The constant of proportionality can be evaluated, but we will not need to use it.

It should be clear that the density is a maximum when and decreases as the distance from to , and indeed an HDR for is clearly a hyperellipsoid centred on , that is, it is of the form

in which the length of each of the axes is in a constant ratio to .

To find an HDR of any particular probability it therefore suffices to find the distribution of , and since is a ratio of sums of squares divided by appropriate numbers of degrees of freedom it seems reasonable to conjecture that

which is indeed so.

6.5.3 Derivation of the F distribution

It is not really necessary to follow this proof that really has got an F distribution, but it is included for completeness.

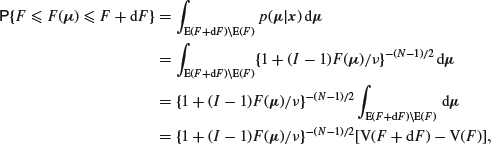
where V(F) is the volume of the hyperellipsoid E(F). At first sight it appears that this is I-dimensional, but because it represents the intersection of a hyperellipsoid in I dimensions with a hyperplane through its centre, which is a hyperellipsoid in (I–1) dimensions. If this is not clear, it may help to note that an ordinary sphere in three-dimensional space cuts a plane in a circle, that is, a sphere in 3–1=2 dimensions. It follows that

and hence

It follows that the density of is proportional to

Comparing this with the standard form in Appendix A and noting that it can be seen that indeed , as asserted.

6.5.4 Relationship to the analysis of variance

This relates to the classical approach to the one-way layout. Note that if

then at the point which represents no treatment effect. Consequently if

then is the probability of an HDR which just includes . It is thus possible to carry out a significance test at level α of the hypothesis that in the sense of Section 4.3 on ‘Lindley’s method’ by rejecting if and only if

This procedure corresponds exactly to the classical analysis of variance (ANOVA) procedure in which you construct a table as follows. First find

It is convenient to write St for . Then find Se by subtraction as it is easily shown that

In computing, it should be noted that it makes no difference if a constant is subtracted from each of the xik and that ST and St can be found by

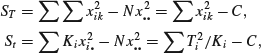
where is the total for treatment i, is the grand total, and C=G2/N is the ‘correction for error’. (Note that these formulae are subject to rounding error if used incautiously.)

The value of is then found easily by setting out a table as follows:

ANOVA Table

We will now consider an example.

6.5.5 Example

Cochran and Cox (1957, Section 4.13) quote the following data from an experiment on the effect of sulphur in reducing scab disease in potatoes. In addition to untreated plots which serve as a control, three amounts of dressing were compared: 300, 600 and 1200 pounds per acre. Both an autumn and a spring application of each treatment were tried, so that in all there were seven distinct treatments. The effectiveness of the treatments were measured by the ‘scab index’, which is (roughly speaking) the average percentage of the area of 100 potatoes taken at random from each plot that is affected with scab. The data are as follows:

There are I = 7 treatments and observations, the grand total being G = 501 (and the grand average being 15.66), the crude sum of squares being and the correction for error C=G2/N=7844. Further

and hence the analysis of variance table is as follows:

ANOVA Table

From tables of the F distribution an F6,25 variable exceeds 3.63 with probability 0.01. Consequently a 99% HDR is

so that and, according to the methodology of Lindley’s method, as described in Section 4.3, the data is very nearly enough to cause the null hypothesis of no treatment effect to be rejected at the 1% level.

The 99% HDR can be re-expressed by noting that is in it if and only if or

that is, if and only if

It is of course difficult to visualize such sets, which is one reason why the significance test mentioned earlier is helpful in giving some ideas as to what is going on. However, as was explained when significance tests were first introduced, they should not be taken too seriously – in most cases, you would expect to see a treatment effect, even if only a small one. One point is that you can get some idea of the size of the treatment effect from the significance level.

6.5.6 Relationship to a simple linear regression model

A way of visualizing the analysis of variance in terms of the simple linear regression model was pointed out by Kelley (1927, p. 178); see also Novick and Jackson (1974, Section 4–7).

Kelley’s work is relevant to a random effects model (sometimes known as a components of variance model or Model II for the analysis of variance). An idea of what this is can be gained by considering an example quoted by Scheffé (1959, Section 7.2). Suppose a machine is used by different workers on different days, being used by worker i on Ki days for , and that the output when worker i uses it on day k is xik. Then it might be reasonable to suppose that

where mi is the ‘true’ mean for the ith worker and eik is his ‘error’ on the kth day. We could then assume that the I workers are a random sample from a large labour pool, instead of contributing fixed if unknown effects. In such a case, all of our knowledge of the xik contributes to knowledge of the distribution of the mi, and so if we want to estimate a particular mi we should take into account the observations for as well as the observations xik. Kelley’s suggestion is that we treat the individual measurements xik as the explanatory variable and the treatment means as the dependent variable, so that the model to be fitted is

where the are error terms of mean zero, or equivalently

In terms of the notation, we used in connection with simple linear regression

In accordance with the theory of simple linear regression, we estimate α and β by, respectively,

so that the regression line takes the form

The point of this formula is that if you were to try one single replicate with another broadly similar treatment to those already tried, you could estimate the overall mean for that treatment not simply by the one observation you have for that treatment, but by a weighted mean of that observation and the overall mean of all observations available to date.

6.5.7 Investigation of contrasts

Often in circumstances where the treatment effect does not appear substantial you may want to make further investigations. Thus, in the aforementioned example about sulphur treatment for potatoes, you might want to see how the effect of any sulphur compares with none, that is, you might like an idea of the size of

More generally, it may be of interest to investigate any contrast, that is, any linear combination

If we then write and

then it is not difficult to show that we can write

where is a quadratic much like St except that has one less dimension and consists of linear combinations of . It follows that

It is then possible to integrate over the I–2 linearly independent components of to get

and then to integrate out to give

(remember that ), where

It follows that .

For example, in the case of the contrast concerned with the main effect of sulphur, d=–14/6–7=–9.3 and Kd={6(1/6)2/4+12/8}–1=6, so that

so that, for example, as a t25 random variable is less than 2.060 in modulus with probability 0.95, a 95% HDR for d is between , that is, (–15.0, –3.7).