5.3 Variances unknown and unequal (Behrens–Fisher problem)

5.3.1 Formulation of the problem

In this section, we are concerned with the most general case of the problem of two normal samples, where neither the means nor the variances are assumed equal. Consequently we have independent vectors and such that

and . This is known as the Behrens–Fisher problem (or sometimes as the Behrens problem or the Fisher–Behrens problem).

It is convenient to use the notation of the previous section, except that sometimes we write and instead of and to avoid using sub-subscripts. In addition, it is useful to define

For the moment, we shall assume independent reference priors uniform in λ, μ, and ψ. Then, just as in Section 2.12 on ‘Normal mean and variance both unknown’, it follows that the posterior distributions of λ and μ are independent and are such that

It is now useful to define T and θ by

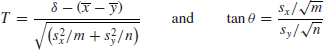
(θ can be taken in the first quadrant). It is then easy to check that

Since θ is known (from the data) and the distributions of Tx and Ty are known, it follows that the distribution of T can be evaluated. This distribution is tabulated and is called Behrens’ (or the Behrens–Fisher or Fisher–Behrens) distribution, and it will be denoted

It was first referred to in Behrens (1929).

5.3.2 Patil’s approximation

Behrens’ distribution turns out to have a rather nasty form, so that the density at any one point can only be found by a complicated integral, although a reasonable approximation was given by Patil (1965). To use this approximation, you need to find

Then approximately

Because b is not necessarily an integer, use of this approximation may necessitate interpolation in tables of the t distribution.

A rather limited table of percentage points of the Behrens distribution based on this approximation is to be found in the tables at the end of the book, but this will often be enough to give some idea as to what is going on. If more percentage points are required or the tables are not available, Patil’s approximation or something like the program in Appendix C has to be used.

5.3.3 Example

Yet again we shall consider the data on the weight growth of rats as in Sections 5.1 and 5.2. Recall that m = 12, n = 7 (so , ), , , Sx=5032, Sy=2552, and hence s2x=457, s2y=425. Therefore,

so that radians using rounded values, and thus . From the tables in the Appendix the 95% point of is 1.91 and that of is 1.88, so the 95% point of must be about 1.89. [The program in Appendix C gives hbehrens(0.9,11,6,39) as the interval (–1.882742, 1.882742).] Consequently a 90% HDR for δ is given by and so is , that is, (0, 38). This is slightly wider than was obtained in the previous section, as is reasonable, because we have made ewer assumptions and can only expect to get less precise conclusions.

The same result can be obtained directly from Patil’s approximation. The required numbers turn out to be f1 = 1.39, f2 = 0.44, b = 8.39, a = 1.03, so that . Interpolating between the 95% percentage points for t8 and t9 (which are 1.860 and 1.833, respectively), the required percentage point for t8.39 is 1.849, and hence a 90% HDR for δ is , giving a very similar answer to that obtained from the tables. [The program in Appendix C gives this probability as .]

Of course, it would need more extensive tables to find, for example, the posterior probability that , but there is no difficulty in principle in doing so. On the other hand, it would be quite complicated to find the Bayes factor for a test of a point null hypothesis such as δ = 0, and since such tests are only to be used with caution in special cases, it would not be likely to be worthwhile.

5.3.4 Substantial prior information

If we do happen to have substantial prior information about the parameters which can reasonably well be approximated by independent normal/chi-squared distributions for and , then the method of this section can usually be extended to include it. All that will happen is that Tx and Ty will be replaced by slightly different quantities with independent t distributions, derived as in Section 2.12 on ‘Normal mean and variance both unknown’. It should be fairly clear how to carry out the details, so no more will be said about this case.