5.2 Variances unknown but equal

5.2.1 Solution using reference priors

We shall now consider the case where we are interested in and we have independent vectors and such that

so that the two samples have a common variance .

We can proceed much as we did in Section 2.12 on ‘Normal mean and variance both unknown’. Begin by defining

For the moment, take independent priors uniform in λ, μ and , that is,

With this prior, the posterior is

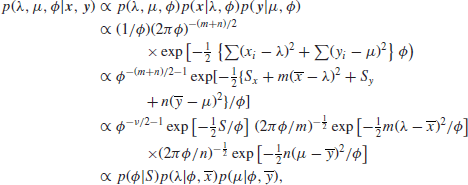
where

It follows that, for given , the parameters λ and μ have independent normal distributions, and hence that the joint density of and δ is

where is an density. The variance can now be integrated out just as in Section 2.12 when we considered a single sample from a normal distribution of unknown variance, giving a very similar conclusion, that is, that if

where , then . Note that the variance estimator s2 is found by adding the sums of squares Sx and Sy about the observed means and dividing by the sum of the corresponding numbers of degrees of freedom, and , and that this latter sum gives the number of degrees of freedom of the resulting Student’s t variable. Another way of looking at it is that s2 is a weighted mean of the variance estimators s2x and s2y given by the two samples with weights proportional to the corresponding degrees of freedom.

5.2.2 Example

This section can be illustrated by using the data considered in the last section on the weight growth of rats, this time supposing (more realistically) that the variances are equal but unknown. We found that Sx=5032, Sy=2552, and so that S = 7584, , s2=7584/17=446 and

Since and , the posterior distribution of δ is given by

From tables of the t distribution it follows, for example, that a 90% HDR for δ is , that is (2, 36). This is not very different from the result in Section 5.2, and indeed it will not usually make a great deal of difference to assume that variances are known unless the samples are very small.

It would also be possible to do other things with this posterior distribution, for example, to find the probability that or to test the point null hypothesis that , but this should be enough to give the idea.

5.2.3 Non-trivial prior information

A simple analysis is possible if we have prior information which, at least approximately, is such that the prior for is and, conditional on , the priors for λ and μ are such that

independently of one another. This means that

Of course, as in any case where conjugate priors provide a nice mathematical theory, it is a question that has to be faced up to in any particular case whether or not a prior of this form is a reasonable approximation to your prior beliefs, and if it is not then a more untidy analysis involving numerical integration will be necessary. The reference prior used earlier is of this form, though it results from the slightly strange choice of values , S0=m0=n0=0. With such a prior, the posterior is

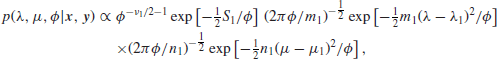
where

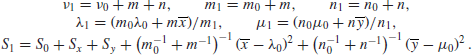
(The formula for S1 takes a little manipulation.)  It is now possible to proceed as in the reference prior case, and so, for given , the parameters λ and μ have independent normal distributions, so that the joint density of and can be written as

where is an density. The variance can now be integrated out as before, giving a very similar result, namely, that if

where , then .

The methodology is sufficiently similar to the case where a reference prior is used that it does not seem necessary to give a numerical example. Of course, the difficulty in using it, in practice, lies in finding appropriate values of the parameters of the prior distribution .