4.7 Exercises on Chapter 4
1. Show that if the prior probability 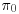 of a hypothesis is close to unity, then the posterior probability p0 satisfies
of a hypothesis is close to unity, then the posterior probability p0 satisfies  and more exactly
and more exactly  .
.
2. Watkins (1986, Section 13.3) reports that theory predicted the existence of a Z particle of mass  GeV, while first experimental results showed its mass to be
GeV, while first experimental results showed its mass to be  GeV. Find the prior and posterior odds and the Bayes ratio for the hypothesis that its mass is less than 93.0 GeV.
GeV. Find the prior and posterior odds and the Bayes ratio for the hypothesis that its mass is less than 93.0 GeV.
3. An experimental station wishes to test whether a growth hormone will increase the yield of wheat above the average value of 100 units per plot produced under currently standard conditions. Twelve plots treated with the hormone give the yields:
![]()
Find the P-value for the hypothesis under consideration.
4. In a genetic experiment, theory predicts that if two genes are on different chromosomes, then the probability of a certain event will be 3/16. In an actual trial, the event occurs 56 times in 300. Use Lindley’s method to decide whether there is enough evidence to reject the hypothesis that the genes are on the same chromosome.
5. With the data in the example in Section 3.4 on ‘The Poisson distribution’, would it be appropriate to reject the hypothesis that the true mean equalled the prior mean (i.e. that  )? [Use Lindley’s method.]
)? [Use Lindley’s method.]
6. Suppose that the standard test statistic 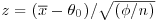 takes the value z=2.5 and that the sample size is n = 100. How close to
takes the value z=2.5 and that the sample size is n = 100. How close to 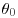 does a value of θ have to be for the value of the normal likelihood function at
does a value of θ have to be for the value of the normal likelihood function at 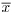 to be within 10% of its value at
to be within 10% of its value at  ?
?
7. Show that the Bayes factor for a test of a point null hypothesis for the normal distribution (where the prior under the alternative hypothesis is also normal) can be expanded in a power series in  as
as
![]()
8. Suppose that x1, x2, 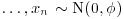 . Show over the interval
. Show over the interval  the likelihood varies by a factor of approximately
the likelihood varies by a factor of approximately
![]()
9. At the beginning of Section 4.5, we saw that under the alternative hypothesis that  the predictive density for
the predictive density for  was
was  , so that
, so that
![]()
Show that a maximum of this density considered as a function of ψ occurs when  , which gives a possible value for ψ if
, which gives a possible value for ψ if 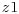 . Hence, show that if
. Hence, show that if  then for any such alternative hypothesis, the Bayes factor satisfies
then for any such alternative hypothesis, the Bayes factor satisfies
![]()
and deduce a bound for p0 (depending on the value of  ).
).
10. In the situation discussed in Section 4.5, for a given P-value (so equivalently for a given z) and assuming that  , at what value of n is the posterior probability of the null hypothesis a minimum.
, at what value of n is the posterior probability of the null hypothesis a minimum.
11. Mendel (1865) reported finding 1850 angular wrinkled seeds to 5474 round or roundish in an experiment in which his theory predicted a ratio of 1:3. Use the method employed for Weldon’s dice data in Section 4.5 to test whether his theory is confirmed by the data. [However, Fisher (1936) cast some doubt on the genuineness of the data.]
12. A window is broken in forcing entry to a house. The refractive index of a piece of glass found at the scene of the crime is x, which is supposed 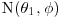 . The refractive index of a piece of glass found on a suspect is y, which is supposed
. The refractive index of a piece of glass found on a suspect is y, which is supposed  . In the process of establishing the guilt or innocence of the suspect, we are interested in investigating whether
. In the process of establishing the guilt or innocence of the suspect, we are interested in investigating whether  is true or not. The prior distributions of
is true or not. The prior distributions of 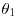 and
and  are both
are both  where
where 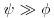 . Write
. Write
![]()
Show that, if H0 is true and 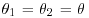 , then
, then  and
and 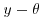 are independent and
are independent and
![]()
By writing  and
and 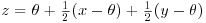 , go on to show that u has an
, go on to show that u has an  distribution and that z has an
distribution and that z has an  , so approximately an
, so approximately an 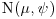 , distribution. Conversely, show that if H0 is false and
, distribution. Conversely, show that if H0 is false and 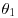 and
and  are assumed independent, then
are assumed independent, then  and
and 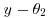 are all independent and
are all independent and
![]()
By writing
![]()
and
![]()
show that in this case u has an  , so approximately an
, so approximately an  , distribution, while z has an
, distribution, while z has an  , so approximately an
, so approximately an  , distribution. Conclude that the Bayes factor is approximately
, distribution. Conclude that the Bayes factor is approximately
![]()
Suppose that the ratio 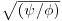 of the standard deviations is 100 and that
of the standard deviations is 100 and that 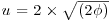 , so that the difference between x and y represents two standard deviations, and that
, so that the difference between x and y represents two standard deviations, and that 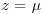 , so that both specimens are of commonly occurring glass. Show that a classical test would reject H0 at the 5% level, but that B=9.57, so that the odds in favour of H0 are multiplied by a factor just below 10.
, so that both specimens are of commonly occurring glass. Show that a classical test would reject H0 at the 5% level, but that B=9.57, so that the odds in favour of H0 are multiplied by a factor just below 10.
[This problem is due to Lindley (1977); see also Shafer (1982). Lindley comments that, ‘What the [classical] test fails to take into account is the extraordinary coincidence of x and y being so close together were the two pieces of glass truly different’.]
[This problem is due to Lindley (1977); see also Shafer (1982). Lindley comments that, ‘What the [classical] test fails to take into account is the extraordinary coincidence of x and y being so close together were the two pieces of glass truly different’.]
13. Lindley (1957) originally discussed his paradox under slightly different assumptions from those made in this book. Follow through the reasoning used in Section 4.5 with  representing a uniform distribution on the interval
representing a uniform distribution on the interval  to find the corresponding Bayes factor assuming that
to find the corresponding Bayes factor assuming that 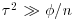 , so that an
, so that an 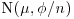 variable lies in this interval with very high probability. Check that your answers are unlikely to disagree with those found in Section 4.5 under the assumption that
variable lies in this interval with very high probability. Check that your answers are unlikely to disagree with those found in Section 4.5 under the assumption that  represents a normal density.
represents a normal density.
14. Express in your own words the arguments given by Jeffreys (1961, Section 5.2) in favour of a Cauchy distribution
![]()
in the problem discussed in the previous question.
15. Suppose that x has a binomial distribution 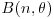 of index n and parameter θ, and that it is desired to test
of index n and parameter θ, and that it is desired to test 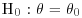 against the alternative hypothesis
against the alternative hypothesis  :
:
a. Find lower bounds on the posterior probability of H0 and on the Bayes factor for H0 versus H1, bounds which are valid for any  .
.
b. If n = 20, 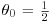 and x = 15 is observed, calculate the (two-tailed) P-value and the lower bound on the posterior probability when the prior probability
and x = 15 is observed, calculate the (two-tailed) P-value and the lower bound on the posterior probability when the prior probability 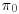 of the null hypothesis is
of the null hypothesis is  .
.
16. Twelve observations from a normal distribution of mean θ and variance  are available, of which the sample mean is 1.2 and the sample variance is 1.1. Compare the Bayes factors in favour of the null hypothesis that
are available, of which the sample mean is 1.2 and the sample variance is 1.1. Compare the Bayes factors in favour of the null hypothesis that 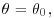 assuming that (a)
assuming that (a)  is unknown and (b) it is known that
is unknown and (b) it is known that 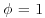 .
.
17. Suppose that in testing a point null hypothesis you find a value of the usual Student’s statistic of 2.4 on 8 degrees of freedom. Would the methodology of Section 4.6 require you to ‘think again’?
18. Which entries in the table in Section 4.5 on ‘Point null hypotheses for the normal distribution’ would, according to the methodology of Section 4.6, cause you to ‘think again’?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
