8.5 Bayesian analysis for an unknown overall mean

In Section 8.2, we derived the posterior for supposing that a priori

where μ was known. We shall now go on to an approach introduced by Lindley (1969) and developed in his contribution to Godambe and Sprott (1971) and in Lindley and Smith (1972) for the case where μ is unknown.

We suppose that

are independent given the and . This is the situation which arises in one way analysis of variance (analysis of variance between and within groups). In either of the practical circumstances described above, the means will be thought to be alike. More specifically, the joint distribution of these means must have the property referred to by de Finetti (1937 or 1974–1975, Section 11.4) as exchangeability; that is, the joint distribution remains invariant under any permutation of the suffices. A famous result in de Finetti (1937) [for a good outline treatment see Bernardo and Smith (1994, Sections 4.2 and 4.3)] says that exchangeability implies that the have the probability structure of a random sample from a distribution. It might seem sensible to add the additional assumption that this distribution is normal (as we often do in statistics). It would then be appropriate to assume that

the being assumed independent for given μ and .

To complete the specification of the prior distribution, it is necessary to discuss μ, and . For the moment, we shall suppose that the two variances are known and that the prior knowledge of μ is weak, so that, over the range for which the likelihood is appreciable, the prior density of μ is constant (cf. Section 2.5).

We thus have

so that

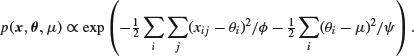
We shall show that we can write the posterior distribution in the form

where the ti are defined by

in which

We thus see that the posterior means of the take the form of a weighted average of the mean (the least-squares estimate) and an overall mean , depending in a natural way on the sample sizes and the ratio of the two variance components. The effect of this weighted average is to shift all the estimates for the sample mean towards the overall mean. It is clear that these estimates are of the same type as the Efron–Morris (or Stein) estimators derived earlier.

The proof of this result is given in Section 8.6, but can be omitted by readers willing to take the result for granted. It must be admitted that the result is mainly of theoretical interest because it is difficult to think of real-life cases where both and are known.

In the case where and are unknown and conjugate (inverse chi-squared) priors are taken for them, somewhat similar results are possible with and in the expression for wj replaced by suitable estimators; the details can be found in Lindley’s contribution to Godambe and Sprott (1971). Unfortunately, while it is possible to use a reference prior for , there are severe difficulties about using a similar prior for . In the words of Lindley, op. cit.,

The difficulty can be viewed mathematically by remarking that if a prior proportional to … which is improper … – is used, then the posterior remains improper whatever size of sample is taken. Heuristically it can be seen that the between-sample variance provides information directly about , – that is, confounded with – and not about itself, so that the extreme form of the prior cannot be overcome by sampling.

We shall discuss numerical methods for use in connection with the hierarchical normal model in Sections 9.2 and 9.4.

8.5.1 Derivation of the posterior

Because

where , we see that

Noting that (because )

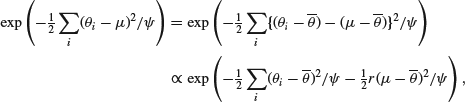
we can integrate over μ to get

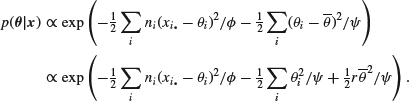
Minus twice the coefficient of in the above exponential is

while the coefficient of of is

from which it follows that if we set

we can write the posterior distribution in the form

where the ti are yet to be determined.

By equating coefficients of we see that

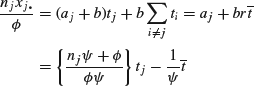
where

Writing

it follows that

so that

where

and so

We have thus proved that the posterior means of the do indeed take the form of a weighted average of the mean (the least-squares estimate) and an overall mean , depending in a natural way on the sample sizes and the ratio of the two variance components and so shift all the estimates for the sample mean towards the overall mean.

A further discussion of related matters can be found in Leonard and Hsu (2001, Section 6.3).