6.3 Regression and the bivariate normal model

6.3.1 The model

The problem we will consider in this section is that of using the values of one variable to explain or predict values of another. We shall refer to an explanatory and a dependent variable, although it is conventional to refer to an independent and a dependent variable. An important reason for preferring the phrase explanatory variable is that the word ‘independent’ if used in this context has nothing to do with the use of the word in the phrase ‘independent random variable’. Some authors, for example, Novick and Jackson (1974, Section 9.1), refer to the dependent variable as the criterion variable. The theory can be applied, for example, to finding a way of predicting the weight (the dependent variable) of typical individuals in terms of their height (the explanatory variable). It should be noted that the relationship which best predicts weight in terms of height will not necessarily be the best relationship for predicting height in terms of weight.

The basic situation and notation are the same as in the last two sections, although in this case there is not the symmetry between the two variables that there was there. We shall suppose that the xs represent the explanatory variable and the ys the dependent variables.

There are two slightly different situations. In the first, the experimenters are free to set the values of xi, whereas in the second both values are random, although one is thought of as having a causal or explanatory relationship with the other. The analysis, however, turns out to be the same in both cases.

The most general model is

where in the first situation described above is a null vector and the distribution of is degenerate. If it is assumed that and have independent priors, so that , then

It is now obvious that we can integrate over to get

Technically, given , the vector is sufficient for and, given , the vector is ancillary for . It follows that insofar as we wish to make inferences about , we may act as if were constant.

6.3.2 Bivariate linear regression

We will now move on to a very important particular case. Suppose that conditional on we have

Thus,

unless one or more of , and are known, in which case the ones that are known can be dropped from . Thus, we are supposing that, on average, the dependence of the ys on the xs is linear. It would be necessary to use rather different methods if there were grounds for thinking, for example, that or that . It is also important to suppose that the ys are homoscedastic, that is, that the variance has the same constant value whatever the value of xi; modifications to the analysis would be necessary if it were thought that, for example, so that the variance increased with xi.

It simplifies some expressions to write as where, of course, , so that and , hence . The model can now be written as

Because a key feature of the model is the regression line on which the expected values lie, the parameter β is usually referred to as the slope and α is sometimes called the intercept, although this term is also sometimes applied to . For the rest of this section, we shall take a reference prior that is independently uniform in α, β and , so that

In addition to the notation used in Sections 6.1 and 6.2, it is helpful to define

It then turns out that

Now since is a constant and the sum of squares can be written as

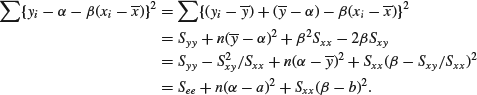
Thus, the joint posterior is

It is now clear that for given b and the posterior for β is , and so we can integrate β out to get

(note the change in the exponent of ).

In Section 2.12 on ‘Normal mean and variance both unknown’, we showed that if

and then

It follows from just the same argument that in this case the posterior for α given and is such that if s2=See/(n–2) then

Similarly the posterior of β can be found be integrating α out to show that

Finally, note that

It should, however, be noted that the posteriors for α and β are not independent, although they are independent for given .

It may be noted that the posterior means of α and β are a and b and that these are the values that minimize the sum of squares

and that See is the minimum sum of squares. This fact is clear because the sum is

and it constitutes the principle of least squares, for which reason a and b are referred to as the least squares estimates of α and β. The regression line

which can be plotted for all x as opposed to just those xi observed, is called the line of best fit for y on x. The principle is very old; it was probably first published by Legendre but first discovered by Gauss; for its history see Harter (1974, 1975, 1976). It should be noted that the line of best fit for y on x is not, in general, the same as the line of best fit for x on y.

6.3.3 Example

This example goes to show that what I naïvely thought to be true of York’s weather is, in fact, false. I guessed that if November was wet, the same thing would be true in December, and so I thought I would try and see how far this December’s rainfall could be predicted in terms of November’s. It turns out that the two are in fact negatively correlated, so that if November is very wet there is a slight indication that December will be on the dry side. However, the data (given in mm) serves quite as well to indicate the method.

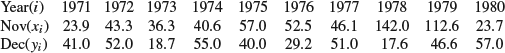
It turns out that , , Sxx=13, 539, Syy=1889 and Sxy=–2178, so that

It follows that

Since the 75th percentile of t8 is 0.706, it follows that a 50% HDR for the intercept α is , that is, (37.7, 43.9). Similarly, a 50% HDR for the slope β is , that is, (–0.245, –0.077). Further, from tables of values of corresponding to HDRs for , an interval of posterior probability 50% for the variance is from 1538/11.079 to 1538/5.552, that is, (139, 277).

Very often the slope β is of more importance than the intercept α. Thus, in the above example, the fact that the slope is negative with high probability corresponds to the conclusion that high rainfall in November indicates that there is less likely to be high rainfall in December, as was mentioned earlier.

6.3.4 Case of known variance

If, which is not very likely, you should happen to know the variance , the problem is even simpler. In this case, it is easy to deduce that (with the same priors for α and β)

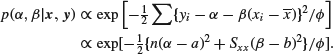
It is clear that in this case the posteriors for α and β are independent and such that and .

6.3.5 The mean value at a given value of the explanatory variable

Sometimes there are other quantities of interest than α, β and . For example, you might want to know what the expected value of y is at a given value of x. A particular case would arise if you wanted estimate the average weight of women of a certain height on the basis of data on the heights and weights of n individuals. Similarly, you might want to know about the value of the parameter in the original formulation (which corresponds to the particular value x = 0). Suppose that the parameter of interest is

Now we know that for given , , x0 and

independently of one another. It follows that, given the same values,

It is now easy to deduce from the fact that has a (multiple of an) inverse chi-squared distribution. The same arguments used in Section 2.12 on ‘Normal mean and variance both unknown’ can be used to deduce that

In particular, setting x0=0 and writing we get

6.3.6 Prediction of observations at a given value of the explanatory variable

It should be noted that if you are interested in the distribution of a potential observation at a value x=x0, that is, the predictive distribution, then the result is slightly different. The mean of such observations conditional on , and x0 is still , but since

in addition to the above distribution for , it follows that

and so on integrating out

6.3.7 Continuation of the example

To find the mean rainfall to be expected in December in a year when there are x0=46.1 mm in November, we first find and , and hence . Then the distribution of the expected value at x=x0 is N(42.7, 4.602). On the other hand, in single years in which the rainfall in November is 46.1, there is a greater variation in the December rainfall than the variance for the mean of 4.602=21.2 implies – in fact and the corresponding variance is 14.62=213.2.

6.3.8 Multiple regression

Very often there is more than one explanatory variable, and we want to predict the value of y using the values of two or more variables x(1), x(2), etc. It is not difficult to adapt the method described earlier to estimate the parameters in a model such as

although you will find some complications unless it happens that

For this reason, it is best to deal with such multiple regression problems by using matrix analysis. Readers who are interested will find a brief introduction to this topic in Section 6.7, while a full account can be found in Box and Tiao (1992).

6.3.9 Polynomial regression

A difficult problem which will not be discussed in any detail is that of polynomial regression, that is, of of fitting a model

where all the parameters, including the degree r of the polynomial are unknown a priori. Some relevant references are Jeffreys (1961, Sections 5.9–5.92) and Sprent (1969, Sections 5.4, 5.5). There is also an interesting discussion in Meyer and Collier (1970, p. 114 et seq.) in which Lindley starts by remarking:

I agree the problem of fitting a polynomial to the data is one that at the moment I can’t fit very conveniently to the Bayesian analysis. I have prior beliefs in the smoothness of the polynomial. We need to express this idea quantitatively, but I don’t know how to do it. We could bring in our prior opinion that some of the regression coefficients are very small.

Subsequently, a Bayesian approach to this problem has been developed by Young (1977).