6.1 Theory of the correlation coefficient

6.1.1 Definitions

The standard measure of association between two random variables, which was first mentioned in Section 1.5 on ‘Means and Variances’, is the correlation coefficient

It is used to measure the strength of linear association between two variables, most commonly in the case where it might be expected that both have, at least approximately, a normal distribution. It is most important in cases where it is not thought that either variable is dependent on the other. One example of its use would be an investigation of the relationship between the height and the weight of individuals in a population, and another would be in finding how closely related barometric gradients and wind velocities were. You should, however, be warned that it is very easy to conclude that measurements are closely related because they have a high correlation, when, in fact, the relationship is due to their having a common time trend or a common cause and there is no close relationship between the two (see the relationship between the growth of money supply and Scottish dysentery as pointed out in a letter to The Times dated 6 April 1977). You should also be aware that two closely related variables can have a low correlation if the relationship between them is highly non-linear.

We suppose, then, that we have a set of n ordered pairs of observations, the pairs being independent of one another but members of the same pair being, in general, not independent. We shall denote these observations (xi, yi) and, as usual, we shall write and . Further, suppose that these pairs have a bivariate normal distribution with

and we shall use the notation

(Sxx and Syy have previously been denoted Sx and Sy), and

It is also useful to define the sample correlation coefficient r by

so that .

We shall show that, with standard reference priors for λ, μ, and , a reasonable approximation to the posterior density of ρ is given by

where is its prior density. Making the substitution

we will go on to show that after another approximation

These results will be derived after quite a complicated series of substitutions [due to Fisher (1915, 1921)]. Readers who are prepared to take these results for granted can omit the rest of this section.

6.1.2 Approximate posterior distribution of the correlation coefficient

As before, we shall have use for the formulae

and also for a similar one not used before

Now the (joint) density function of a single pair (x, y) of observations from a bivariate normal distribution is

where

and hence the joint density of the vector is

where

It follows that the vector is sufficient for . For the moment, we shall use independent priors of a simple form. For λ, μ, and , we shall take the standard reference priors, and for the moment we shall use a perfectly general prior for ρ, so that

and hence

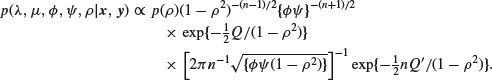
The last factor is evidently the (joint) density of λ and μ considered as bivariate normal with means and , variances and and correlation ρ. Consequently it integrates to unity, and so as the first factor does not depend on λ or μ

To integrate and out, it is convenient to define

so that and . The Jacobian is

and hence

where

The substitution (so that ) reduces the integral over to a standard gamma function integral, and hence we can deduce that

Finally, integrating over ω

By substituting for ω it is easily checked that the integral from 0 to 1 is equal to that from 1 to , so that as constant multiples are irrelevant, the lower limit of the integral can be taken to be 1 rather than 0.

By substituting , the integral can be put in the alternative form

The exact distribution corresponding to has been tabulated in David (1954), but for most purposes it suffices to use an approximation. The usual way to proceed is by yet a further substitution, in terms of u where , but this is rather messy and gives more than is necessary for a first-order approximation. Instead, note that for small t

while the contribution to the integral from values where t is large will, at least for large n, be negligible. Using this approximation

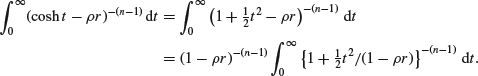
On substituting

the integral is seen to be proportional to

Since the integral in this last expression does not depend on ρ, we can conclude that

Although evaluation of the constant of proportionality would still require the use of numerical methods, it is much simpler to calculate the distribution of ρ using this expression than to have to evaluate an integral for every value of ρ. In fact, the approximation is quite good [some numerical comparisons can be found in Box and Tiao (1992, Section 8.4.8)].

6.1.3 The hyperbolic tangent substitution

Although the exact mode does not usually occur at , it is easily seen that for plausible choices of the prior , the approximate density derived earlier is greatest when ρ is near r. However, except when r = 0, this distribution is asymmetrical. Its asymmetry can be reduced by writing

so that and

It follows that

If n is large, since the factor does not depend on n, it may be regarded as approximately constant over the range over which is appreciably different from zero, so that

Finally put

and note that if ζ is close to z then . Putting this into the expression for and using the exponential limit

so that approximately , or equivalently

A slightly better approximation to the mean and variance can be found by using approximations based on the likelihood as in Section 3.10. If we take a uniform prior for ρ or at least assume that the prior does not vary appreciably over the range of values of interest, we get

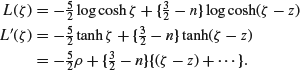
We can now approximate ρ by r (we could write and so get a better approximation, but it is not worth it). We can also approximate by n, so getting the root of the likelihood equation as

Further

so that again approximating ρ by r, we have at

It follows that the distribution of ζ is given slightly more accurately by

This approximation differs a little from that usually given by classical statisticians, who usually quote the variance as (n–3)–1, but the difference is not of great importance.

6.1.4 Reference prior

Clearly, the results will be simplest if the prior used has the form

for some c. The simplest choice is to take c = 0, that is, a uniform prior with , and it seems quite a reasonable choice. It is possible to use the multi-parameter version of Jeffreys’ rule to find a prior for , though it is not wholly simple. The easiest way is to write for the covariance and to work in terms of the inverse of the variance–covariance matrix, that is, in terms of where

It turns out that , where Δ is the determinant , and that the Jacobian determinant

so that . Finally, transforming to the parameters that are really of interest, it transpires that

which corresponds to the choice and the standard reference priors for and .

6.1.5 Incorporation of prior information

It is not difficult to adapt the aforementioned analysis to the case where prior information from the conjugate family [i.e. inverse chi-squared for and and of the form for ρ] is available. In practice, this information will usually be available in the form of previous measurements of a similar type and in this case it is best dealt with by transforming all the information about ρ into statements about so that the theory we have built up for the normal distribution can be used.