1. Suppose that 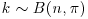. Find the standardized likelihood as a function of π for given k. Which of the distributions listed in Appendix A does this represent?

2. Suppose we are given the 12 observations from a normal distribution:
  15.644, 16.437, 17.287, 14.448, 15.308, 15.169,
  18.123, 17.635, 17.259, 16.311, 15.390, 17.252,
and we are told that the variance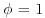 . Find a 90% HDR for the posterior distribution of the mean assuming the usual reference prior.

3. With the same data as in the previous question, what is the predictive distribution for a possible future observation x?

4. A random sample of size n is to be taken from an distribution where is known. How large must n be to reduce the posterior variance of to the fraction of its original value (where k> 1)?

5. Your prior beliefs about a quantity θ are such that

A random sample of size 25 is taken from an distribution and the mean of the observations is observed to be 0.33. Find a 95% HDR for θ.

6. Suppose that you have prior beliefs about an unknown quantity θ which can be approximated by an 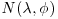distribution, while my beliefs can be approximated by an 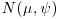distribution. Suppose further that the reasons that have led us to these conclusions do not overlap with one another. What distribution should represent our beliefs about θ when we take into account all the information available to both of us?

7. Prove the theorem quoted without proof in Section 2.4.

8. Under what circumstances can a likelihood arising from a distribution in the exponential family be expressed in data translated form?

9. Suppose that you are interested in investigating how variable the performance of schoolchildren on a new mathematics test, and that you begin by trying this test out on children in 12 similar schools. It turns out that the average standard deviation is about 10 marks. You then want to try the test on a thirteenth school, which is fairly similar to those you have already investigated, and you reckon that the data on the other schools gives you a prior for the variance in this new school which has a mean of 100 and is worth eight direct observations on the school. What is the posterior distribution for the variance if you then observe a sample of size 30 from the school of which the standard deviation is 13.2? Give an interval in which the variance lies with 90% posterior probability.

10. The following are the dried weights of a number of plants (in g) from a batch of seeds:
 4.17, 5.58, 5.18, 6.11, 4.50, 4.61, 5.17, 4.53, 5.33, 5.14.
Give 90% HDRs for the mean and variance of the population from which they come.

11. Find a sufficient statistic for μ given an n-sample 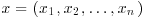from the exponential distribution

where the parameter μ can take any value in .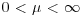

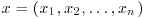12. Find a (two-dimensional) sufficient statistic for given an n-sample from the two-parameter gamma distribution

where the parameters α and can take any values in , .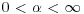

13. Find a family of conjugate priors for the likelihood 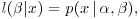where 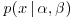is as in the previous question, but α is known.

14. Show that the tangent of a random angle (i.e. one which is uniformly distributed on 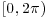) has a Cauchy distribution C(0, 1).

15. Suppose that the vector has a trinomial distribution depending on the index n and the parameter where 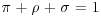, that is

Show that this distribution is in the two-parameter exponential family.

16. Suppose that the results of a certain test are known, on the basis of general theory, to be normally distributed about the same mean μ with the same variance , neither of which is known. Suppose further that your prior beliefs about 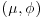can be represented by a normal/chi-squared distribution with

Now suppose that 100 observations are obtained from the population with mean 89 and sample variance s2=30. Find the posterior distribution of 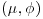. Compare 50% prior and posterior HDRs for μ.

17. Suppose that your prior for θ is a 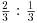mixture of 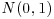and and that a single observation 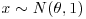turns out to equal 2. What is your posterior probability that ?

18. Establish the formula

where n1=n0+n and 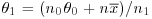, which was quoted in Section 2.13 as providing a formula for the parameter S1 of the posterior distribution in the case where both mean and variance are unknown which is less susceptible to rounding errors.