2.12 Normal mean and variance both unknown

2.12.1 Formulation of the problem

It is much more realistic to suppose that both parameters of a normal distribution are unknown rather than just one. So we consider the case where we have a set of observations which are with θ and both unknown. Clearly,

from which it follows that the density is in the two-parameter exponential family as defined above. Further

wherein we define

(rather than as as in the case where the mean is known to be equal to μ). It is also convenient to define

(rather than s2=S/n as in the case where the mean is known).

It is worth noting that the two-dimensional vector or equivalently is clearly sufficient for given X.

Because this case can get quite complicated, we shall first consider the case of an indifference or ‘reference’ prior. It is usual to take

which is the product of the reference prior for θ and the reference prior for . The justification for this is that it seems unlikely that if you knew very little about either the mean or the variance, then being given information about the one would affect your judgements about the other. (Other possible priors will be discussed later.) If we do take this reference prior, then

For reasons which will appear later, it is convenient to set

in the power of , but not in the exponential, so that

2.12.2 Marginal distribution of the mean

Now in many real problems what interests us is the mean θ, and is what is referred to as a nuisance parameter. In classical (sampling theory) statistics, nuisance parameters can be a real nuisance, but there is (at least in principle) no problem from a Bayesian viewpoint. All we need to do is to find the marginal (posterior) distribution of θ, and you should recall from Section 1.4 on ‘Several Random Variables’ that

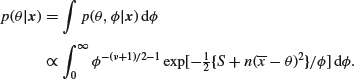
This integral is not too bad – all you need to do is to substitute

where

and it reduces to a standard gamma function integral

It follows that

which is the required posterior distribution of θ. However, this is not the most convenient way to express the result. It is usual to define

where (as defined earlier) . Because the Jacobian of the transformation from θ to t is a constant, the posterior density of t is given by

A glance at Appendix A will show that this is the density of a random variable with Student’s   distribution on ν degrees of freedom, so that we can write . The fact that the distribution of t depends on the single parameter ν makes it sensible to express the result in terms of this distribution rather than that of θ itself, which depends on and S as well as on ν, and is consequently more complicated to tabulate. Note that as the standard exponential limit shows that the density of t is ultimately proportional to , which is the standard normal form. On the other hand, if we see that t has a standard Cauchy distribution C(0, 1), or equivalently that .

Because the density of Student’s t  is symmetric about the origin, an HDR is also symmetric about the origin, and so can be found simply from a table of percentage points.

2.12.3 Example of the posterior density for the mean

Consider the data on uterine weight of rats introduced earlier in Section 2.8 on ‘HDRs for the Normal Variance.’ With those data, n=20, , and , so that and

We can deduce that that the posterior distribution of the true mean θ is given by

In principle, this tells us all we can deduce from the data if we have no very definite prior knowledge. It can help to understand what this means by looking for highest density regions. From tables of the t  distribution the value exceeded by with probability 0.025 is . It follows that a 95% HDR for θ is , that is the interval (18, 24).

2.12.4 Marginal distribution of the variance

If we require knowledge about rather than θ, we use

as the last integral is that of a normal density. It follows that the posterior density of the variance is . Except that n is replaced by the conclusion is the same as in the case where the mean is known. Similar considerations to those which arose when the mean was known make it preferable to use HDRs based on log chi-squared, though with a different number of degrees of freedom.

2.12.5 Example of the posterior density of the variance

With the same data as before, if the mean is not known (which in real life it almost certainly would not be), the posterior density for the variance is . Some idea of the meaning of this can be got from looking for a 95% HDR. Because values of corresponding to an HDR for are found from the tables in the Appendix to be 9.267 and 33.921, a 95% HDR lies between 664/33.921 and 664/9.267, that is the interval (20, 72). It may be worth noting that this does not differ all that much from the interval (19, 67) which we found on the assumption that the mean was known.

2.12.6 Conditional density of the mean for given variance

We will find it useful in Section 2.13 to write the posterior in the form

Since

this implies that

which as the density integrates to unity implies that

that is that, for given and X, the distribution of the mean θ is . This is the result we might have expected from our investigations of the case where the variance is known, although this time we have arrived at the result from conditioning on the variance in the case where neither parameter is truly known.

A distribution for the two-dimensional vector of this form, in which has (a multiple of an) inverse chi-squared distribution and, for given , θ has a normal distribution, will be referred to as a normal/chi-squared distribution, although it is more commonly referred to as normal gamma or normal inverse gamma. (The chi-squared distribution is used to avoid unnecessary complications.)

It is possible to try to look at the joint posterior density of θ and , but two-dimensional distributions can be hard to visualize in the absence of independence, although numerical techniques can help. Some idea of an approach to this can be got from Box and Tiao (1992, Section 2.4).