2.9 The role of sufficiency

2.9.1 Definition of sufficiency

When we considered the normal variance with known mean, we found that the posterior distribution depended on the data only through the single number S. It often turns out that the data can be reduced in a similar way to one or two numbers, and as long as we know them we can forget the rest of the data. It is this notion that underlies the formal definition of sufficiency.

Suppose observations are made with a view to gaining knowledge about a parameter θ, and that

is a function of the observations. We call such a function a statistic. We often suppose that t is real valued, but it is sometimes vector valued. Using the formulae in Section 1.4 on ‘Several Random Variables’ and the fact that once we know x we automatically know the value of t, we see that for any statistic t

However, it sometimes happens that

does not depend on θ, so that

If this happens, we say that t is a sufficient statistic for θ given X, often abbreviated by saying that t is sufficient for θ. It is occasionally useful to have a further definition as follows: a statistic whose density does not depend on θ is said to be ancillary for θ.

2.9.2 Neyman’s factorization theorem

The following theorem is frequently used in finding sufficient statistics:

Theorem 2.2 A statistic t is sufficient for θ given X if and only if there are functions f and g such that

where .

Proof. If t is sufficient for θ given we may take

Conversely, if the condition holds, then, in the discrete case, since once x is known then t is known,

We may then sum both sides of the equation over all values of X such that to get

where G(t) is obtained by summing over all these values of X, using the formula

In the continuous case, write

Then

so that on differentiating with respect to t we find that

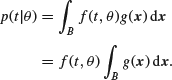
Writing G(t) for the last integral, we get the same result as in the discrete case, viz.

From this it follows that

Considering now any one value of X such that and substituting in the equation in the statement of the theorem we obtain

Since whether t is sufficient or not

we see that

Since the right-hand side does not depend on θ, it follows that t is indeed sufficient, and the theorem is proved.

2.9.3 Sufficiency principle

Theorem 2.3 A statistic t is sufficient for θ given X if and only if

whenever (where the constant of proportionality does not, of course, depend on θ).

Proof. If t is sufficient for θ given X then

Conversely, if the condition holds then

so that for some function

The theorem now follows from the Factorization Theorem.

Corollary 2.1 For any prior distribution, the posterior distribution of θ given X is the same as the posterior distribution of θ given a sufficient statistic t.

Proof. From Bayes’ Theorem is proportional to ; they must then be equal as they both integrate or sum to unity.

Corollary 2.2 If a statistic is such that whenever , then it is sufficient for θ given X.

Proof. By summing or integrating over all X such that , it follows that

the summations being over all such that . The result now follows from the theorem.

2.9.4 Examples

Normal variance. In the case where the xi are normal of known mean μ and unknown variance , we noted that

where . It follows from the Factorization Theorem that S is sufficient for μ given X. Moreover, we can verify the Sufficiency Principle as follows. If we had simply been given the value of S without being told the values of separately, we could have noted that for each i

so that is a sum of squares of n independent variables. Now a distribution is often defined as being the distribution of the sum of squares of n random variables with an distribution, and the density of can be deduced from this. It follows that and hence if then

Using the change of variable rule it is then easily seen that

We can thus verify the Sufficiency Principle in this particular case because

Exponential distribution. Let us suppose that xi () are independently distributed with an exponential distribution (see under the gamma distribution in Appendix A) so that or equivalently . Then

where . It follows from the Factorization Theorem that S is sufficient for θ given S. It is also possible to verify the Sufficiency Principle in this case. In this case it is not hard to show that so that

and we find

Poisson case. Recall that the integer-valued random variable x is said to have a Poisson distribution of mean λ [denoted ] if

We shall consider the Poisson distribution in more detail later in the book. For the moment, all that matters is that it often serves as a model for the number of occurrences of a rare event, for example for the number of times the King’s Arms on the riverbank at York is flooded in a year. Then if have independent Poisson distributions with the same mean (so could, e.g. represent the numbers of floods in several successive years), it is easily seen that

where

It follows from the Factorization Theorem that T is sufficient for λ given X. Moreover, we can verify the Sufficiency Principle as follows. If we had simply been given the value of T without being given the values of the xi separately, we could have noted that a sum of independent Poisson distributions has a Poisson distribution with mean the sum of the means (see question 7 on Chapter 1), so that

and hence,

in accordance with the sufficiency principle.

2.9.5 Order statistics and minimal sufficient statistics

It may be noted that it is easy to see that whenever consists of independently identically distributed observations whose distribution depends on a parameter θ, then the order statistic

which consists of the values of the xi arranged in increasing order, so that

is sufficient for θ given X.

This helps to underline the fact that there is, in general, no such thing as a unique sufficient statistic. Indeed, if t is sufficient for θ given X, then so is (t, u) for any statistic . If t is a function of all other sufficient statistics that can be constructed, so that no further reduction is possible, then t is said to be minimal sufficient. Even a minimal sufficient statistic is not unique, since any one function of such a statistic is itself minimal sufficient.

It is not obvious that a minimal sufficient statistic always exists, but in fact, it does. Although the result is more important than the proof. we shall now prove this. We define a statistic which is a set, rather than a real number or a vector, by

Then it follows from Corollary 2.2 to the Sufficiency Principle that u is sufficient. Further, if is any other sufficient statistic, then by the same principle whenever we have

and hence, , so that u is a function of v. It follows that u is minimal sufficient. We can now conclude that the condition that

if and only if

is equivalent to the condition that t is minimal sufficient.

2.9.6 Examples on minimal sufficiency

Normal variance. In the case where the xi are independently where μ is known but is unknown, then S is not merely sufficient but minimal sufficient.

Poisson case. In the case where the xi are independently , then T is not merely sufficient but minimal sufficient.

Cauchy distribution. We say that x has a Cauchy distribution with location parameter θ and scale parameter 1, denoted if it has density

It is hard to find examples of real data which follow a Cauchy distribution, but the distribution often turns up in counter-examples in theoretical statistics (e.g. a mean of n variables with a C distribution has itself a C distribution and does not tend to normality as n tends to infinity in apparent contradiction of the Central Limit Theorem). Suppose that are independently C. Then if we must have

By comparison of the coefficients of the constant of proportionality must be 1 and by comparison of the zeroes of both sides considered as polynomials in θ, namely, and respectively, we see that the must be a permutation of the xk and hence the order statistics and of and X are equal. It follows that the order statistic is a minimal sufficient statistic, and in particular there is no one-dimensional sufficient statistic. This sort of situation is unusual with the commoner statistical distributions, but you should be aware that it can arise, even if you find the above proof confusing.

A useful reference for advanced workers in this area is Huzurbazar (1976).