2.7 Normal variance

2.7.1 A suitable prior for the normal variance

Suppose that we have an n-sample from where the variance is unknown but the mean μ is known. Then clearly

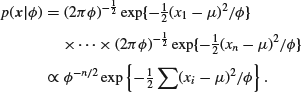
On writing

(remember that μ is known; we shall use a slightly different notation when it is not), we see that

In principle, we might have any form of prior distribution for the variance . However, if we are to be able to deal easily with the posterior distribution (and, e.g. to be able to find HDRs easily from tables), it helps if the posterior distribution is of a ‘nice’ form. This will certainly happen if the prior is of a similar form to the likelihood, namely,

where κ and S0 are suitable constants. For reasons which will emerge, it is convenient to write so that

leading to the posterior distribution

Although it is unlikely that our true prior beliefs are exactly represented by such a density, it is quite often the case that they can be reasonably well approximated by something of this form, and when this is so the calculations become notably simpler.

This distribution is, in fact, closely related to one of the best known continuous distributions in statistics (after the normal distribution), namely, the chi-squared distribution or distribution. This is seen more clearly if we work in terms of the precision instead of in terms of the variance , since, using the change of variable rule introduced in Section 1.3 on ‘Random Variables’,

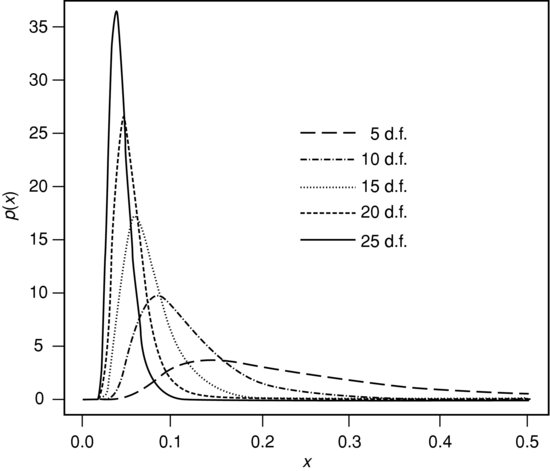
Figure 2.1 Examples of inverse chi-squared densities.

This is now very close to the form of the chi-squared distribution (see Appendix A or indeed any elementary textbook on statistics). It is, in fact, a very simple further step (left as an exercise!) to check that (for given X)

that is has a distribution on degrees of freedom. [The term ‘degrees of freedom’ is hallowed by tradition, but is just a name for a parameter.]  We usually indicate this by writing

and saying that has (a multiple of) an inverse chi-squared distribution.

Clearly the same argument can be applied to the prior distribution, so our prior assumption is that

It may be that you cannot find suitable values of the parameters ν and S0, so that a distribution of this type represents your prior beliefs, but clearly if values can be chosen, so that they are reasonably well approximated, it is convenient. Usually, the approximation need not be too close since, after all, the chances are that the likelihood will dominate the prior. In fitting a plausible prior one possible approach is to consider the mean and variance of your prior distribution and then choose ν and S0, so that

Inverse chi-squared distributions (and variables which have such a distribution apart from a constant multiple) often occur in Bayesian statistics, although the inverse chi-squared (as opposed to the chi-squared) distribution rarely occurs in classical statistics. Some of its properties are described in Appendix A, and its density for typical values of ν (and S0=1) is illustrated in Figure 2.1

2.7.2 Reference prior for the normal variance

The next thing to investigate is whether there is something which we can regard as a reference prior by finding a scale of measurement in which the likelihood is data translated. For this purpose (and others), it is convenient to define the sample standard deviation s by

(again we shall use a different definition when μ is unknown). Then

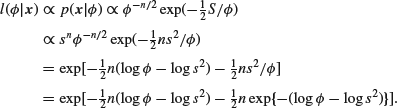
This is of data translated form

(cf. Section 2.4 on ‘Dominant likelihoods’) with

The general argument about data translated likelihoods now suggests that we take as reference prior an improper density which is locally uniform in , that is , which, in terms of corresponds to

and so to

(Although the above argument is complicated, and a similarly complicated example will occur in the case of the uniform distribution in 3.6, there will be no other difficult arguments about data translated likelihoods.)

This prior (which was first mentioned in Section 2.4 on dominant likelihoods) is, in fact, a particular case of the priors of the form , which we were considering earlier, in which and S0=0. Use of the reference prior results in a posterior distribution

which again is a particular case of the distribution found before, and is quite easy to use.

You should perhaps be warned that inferences about variances are not as robust as inferences about means if the underlying distribution turns out to be only approximately normal, in the sense that they are more dependent on the precise choice of prior distribution.