10.5 Reversible jump Markov chain Monte Carlo

The Metropolis–Hastings algorithm introduced in Section 9.6 can be generalized to deal with a situation in which we have a number of available models, each with unknown parameters, and we wish to choose between them.

The basic idea is that as well as considering moves within a model as in the basic Metropolis–Hastings algorithm we also consider possible moves between models. We can regard the chain as moving between states which are specified by a model and a set of parameters for that model. For the time being, we shall suppose that we have two models M(1) with parameters and M(2) with parameters , so that at time t we have model M(i[t]) with parameters .

10.5.1 RJMCMC algorithm

1. Initialize by setting t=0 and choosing i[0] and hence model M(i[0]), and then initial parameters .

2. For

a. Update the parameters of the current model M(i[t–1]) as in the usual Metropolis–Hastings algorithm.

b. Propose to move to a new model with parameters . Calculate the acceptance probability for the move and decide whether to accept or reject the new model (and parameter values).

An example arises in connection with the coal-mining disaster data in which we could consider a model M(1) in which all the data are supposed to be such that for and compare it with the model M(2) discussed in Section 9.4 in which we suppose there is an unknown value k such that for and for (with and unknown). In this case typical states of the chain would be and .

A problem which is immediately seen with models M(1) and M(2) described earlier is that while M(1) has only one unknown parameter, namely , M(2) has three, namely . We accordingly add auxiliary variables to the parameters of model M1, so that the parameter spaces of the two models are of the same dimension. The auxiliary variables do not affect the modelling of the data but allow a one-to-one mapping between the two parameter spaces. We can easily map from the parameters of M(2) to M(1) by setting , but in order to map from the parameters of M(1) to uniquely determined parameters M(2) we need these auxiliary variables. We can then, for example, take , and k=w, where the random variables v and w are chosen to have suitable distributions.

Because of the fact that we change the variables we use, we need to re-examine the detailed balance equation

from which we deduced the Metropolis–Hastings algorithm in Section 9.6. We note that since we need to work in terms of probability elements in the continuous multivariate case this should be thought of as

In one dimension, the ratio of differentials would give rise to an ordinary derivative, but the analogue in many dimensions is, of course, the Jacobian . For this reason, we find

Since the models have different parameters, it is clear that the priors cannot cancel out and so must be proper.

We can give a more explicit form to the probability of switching as follows. Let be the parameters of a model M(i) and let be the associated auxiliary variables. Let be the parameters of a model M(j) and let be the associated auxiliary variables. Write and . Let be a proposal distribution for and let be the proposal distribution for . Then the probability of moving from model i with parameters to model j with parameters is

where q(i | j) is the probability that a change of model from model i results in model j and is the Jacobian.

In the case of the coal-mining disasters, we have only two possible models, so that q(2 | 1)=q(1 | 2)=1. Further, as , and k=w, we find

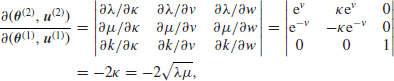
so that, depending on which way a jump is proposed, either or .

In this case, a suitable proposal density is obtained by giving v a normal distribution with mean zero and a suitable variance, so , and w a discrete uniform distribution over (2, n–1), so that . Since is null, we may take . In fact, it turns out that there is strong evidence for the existence of a change point; if the chain is started in model M(2) it always remains in that model (and the change point still being some time in 1889), although, if we allow the possibility of more than one change point, then Green (1995) shows that there is weak evidence for a second change point.

Another case where RJMCMC can be applied is in mixture models where we are unsure how many components are present. As a simple case, we might wish to tell whether a data set X consists of a single normal population of mean 0 or a 50:50 mixture of populations with mean 0 but different variances. More generally, we could allow for more components, for different means and for variable mixing coefficients. The method can also be applied in choosing between various regression models. In cases where there are m> 2 models, values of q(j | i) will have to be supplied, but in some cases it will suffice simply to take q(j | i)=1/(m–1) for all i and j (with ), or at least to make all jumps to models which are in some sense ‘adjacent’ equally likely.

Some more details about this approach, including a detailed treatment of the coal-mining disaster data, can be found in Green (1995); see also Richardson and Green (1997).

More information can be found in Fan and Sisson (2011) or Gamerman and Lopes (2006). RJMCMC is in the process of being incorporated into WinBUGS; for information about this see the website associated with this book.